2.4 Cyclic Groups and the Order of an Element
1. If o(g) = n, we use Theorem 8: gk generates G = g
g  if and only if gcd (k, n) = 1.
if and only if gcd (k, n) = 1.
a. o(g) = 5. Then G = gk
gk  if k = 1, 2, 3, 4.
if k = 1, 2, 3, 4.
c. o(g) = 16. Then G = gk
gk  if k = 1, 3, 5, 7, 9, 11, 13, 15.
if k = 1, 3, 5, 7, 9, 11, 13, 15.
2. Since 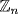 is cyclic and
is cyclic and 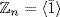 , the solution to Exercise 1 applies.
, the solution to Exercise 1 applies.
a. 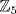 has generators
has generators 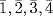 .
.
2. 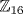 has generators
has generators 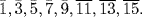
3. a. G = g
g  , o(g) =∞. We claim g and g−1 are the only generators. Note that gk = (g−1)−k for all
, o(g) =∞. We claim g and g−1 are the only generators. Note that gk = (g−1)−k for all  , so G =
, so G = g−1
g−1  . Suppose G =
. Suppose G = gm
gm  . Then g
. Then g
 gm
gm  , say
, say  . Thus g1 = gmk so 1 = mk by Theorem 3. Since m and k are integers, this shows m = ± 1.
. Thus g1 = gmk so 1 = mk by Theorem 3. Since m and k are integers, this shows m = ± 1.
4.
a. . We have
. We have  , so
, so 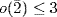 . As to
. As to  :
: 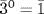 ,
, 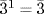 ,
, 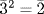 ,
,  ,
, 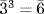 ,
,  ,
, 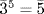 . Thus
. Thus 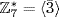 .
.
c. 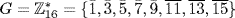 . Here
. Here 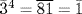 , so
, so 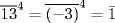 . Similarly
. Similarly 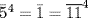 ,
, 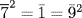 , and
, and 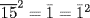 . Thus
. Thus 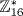 is not cyclic.
is not cyclic.
5. a. No, If 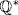 is cyclic, suppose
is cyclic, suppose 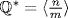 where gcd (m, n) = 1. Then
where gcd (m, n) = 1. Then 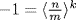 for
for 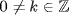 . Now if k < 0, then
. Now if k < 0, then 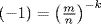 , so we may assume k > 0. Then −mk = nk, and this is impossible for relatively prime m and n, unless n = ± 1, m = ± 1. Then
, so we may assume k > 0. Then −mk = nk, and this is impossible for relatively prime m and n, unless n = ± 1, m = ± 1. Then 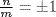 generates
generates 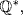 a contradiction.
a contradiction.
7. Given o(g) = 20:
a. 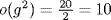 by Theorem 5.
by Theorem 5.
b. 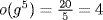 by Theorem 5.
by Theorem 5.
8. a. Each element σ of S5 factors into disjoint cycles in one of the following ways:
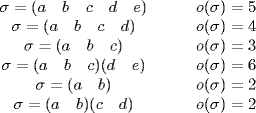
Hence, by Theorem 4, any permutation of the form (a b c)(d e) has maximum order 6.
9.
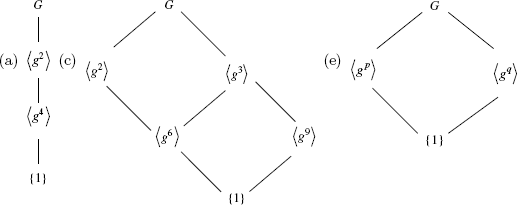
10. a. If o(g) = n and o(h) = m, then (gh)nm = (gn)m(hn)m = 1 because gh = hg.
11. a. If G = a
a  where o(a) = n, let g = ak. Then
where o(a) = n, let g = ak. Then
![]()
13. a. Observe first that g−1 = g if and only if g = 1 or o(g) = 2. Thus all the elements in the product a = g1g2  gn which are not of order 2 (if any) cancel in pairs because G is abelian. Since
gn which are not of order 2 (if any) cancel in pairs because G is abelian. Since 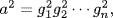 and since 1 and the elements of order 2 (if any) all square to 1, the result follows.
and since 1 and the elements of order 2 (if any) all square to 1, the result follows.
15. We have  a, ab
a, ab ⊆
⊆  a, b
a, b  by Theorem 10 because a
by Theorem 10 because a
 a, b
a, b  and b
and b
 a, b
a, b  . The reverse inclusion follows because a
. The reverse inclusion follows because a
 a, ab
a, ab  and b = a−1(ab)
and b = a−1(ab)
 a, ab
a, ab  . Similarly,
. Similarly,  a, b
a, b =
=  a−1, b−1
a−1, b−1  because a−1, b−1
because a−1, b−1
 a, b
a, b  , and a = (a−1)−1 and b = (b−1)−1 are both in
, and a = (a−1)−1 and b = (b−1)−1 are both in  a−1, b−1
a−1, b−1 .
.
16.
a. We have a = a4(a3)−1  H, so G =
H, so G =  a
a  ⊆ H. Thus H = G.
⊆ H. Thus H = G.
c. We have d = xm + yk with 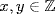 , so ad = (am)x(ak)y
, so ad = (am)x(ak)y  H. Thus
H. Thus  ad
ad  ⊆ H. But d|m, say m = qd, so am = (ad)q
⊆ H. But d|m, say m = qd, so am = (ad)q
 ad
ad  . Similarly ak
. Similarly ak
 ad
ad  , so H =
, so H = ad
ad  by Theorem 10.
by Theorem 10.
e. {(1, 1), (a, b), (a2, b2), (a3, b3)} =  (a, b)
(a, b)  ⊆ H and
⊆ H and
![]()
Then
![]()
Hence K ⊆ H where
![]()
Since K = {(ak, bm)  k + m even}, it is a subgroup containing (a, b) and (a3, b). Hence H ⊆ K, so K = H.
k + m even}, it is a subgroup containing (a, b) and (a3, b). Hence H ⊆ K, so K = H.
17. a. Since X ⊆ Y and Y ⊆  Y
Y  , we have X ⊆
, we have X ⊆  Y
Y  . But
. But  Y
Y is a subgroup, so
is a subgroup, so  X
X ⊆
⊆  Y
Y  by Theorem 10.
by Theorem 10.
19. We have xy−1 = y−1x and x−1y−1 = y−1x−1 for all x, y  X. If
X. If
![]()
then each 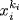 commutes with all the others. Hence each element of
commutes with all the others. Hence each element of  X
X commutes with all the others.
commutes with all the others.
20. If C6 = a
a  and C15 =
and C15 = b
b  , then (a3, b), (a, b3), (a, b) all have order 30. Since (x, y)30 = (x30, y30) = (1, 1) for all (x, y) in C6 × C15, these have maximal order.
, then (a3, b), (a, b3), (a, b) all have order 30. Since (x, y)30 = (x30, y30) = (1, 1) for all (x, y) in C6 × C15, these have maximal order.
21. Each element of S5 factors into cycles in one of the following ways (shown with their orders).
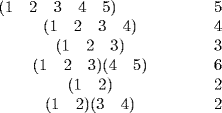
Since lcm(5, 4, 3, 6, 2, 2) = 60, we have σ60 = ε for all σ  S5. On the other hand, if σn = ε for all σ
S5. On the other hand, if σn = ε for all σ  S5, then o(σ) divides n for all σ, and so n is a common multiple of 5, 4, 3, 6, 2, 2. Thus 60 ≤ n.
S5, then o(σ) divides n for all σ, and so n is a common multiple of 5, 4, 3, 6, 2, 2. Thus 60 ≤ n.
23. a. We have (ghg−1)k = ghkg−1 for all k ≥ 1. Hence hk = 1 if and only if (ghg−1)k = 1. It follows that o(h) = o(ghg−1) as in Example 10.
24. a. If h is the only element of order 2 in G, then h = g−1hg for all g  G since (g−1hg)2 = g−1h(gg−1)hg = g−1h2g = g−1g = 1. Thus gh = hg for all g
G since (g−1hg)2 = g−1h(gg−1)hg = g−1h2g = g−1g = 1. Thus gh = hg for all g  G, that is h
G, that is h  Z(G). Note that C4 =
Z(G). Note that C4 = a
a  , o(a) = 4, has such an element: a2.
, o(a) = 4, has such an element: a2.
25. Let G = g
g  and H =
and H = h
h  where o(g) = m and o(h) = n. Since we have |G × H| = |G| |H| = mn, it suffices to show that o((g, h)) = nm. We have (g, h)nm = (gnm, hnm) = (1, 1). If (g, h)k = (1, 1), then gk = 1 and hk = 1, so m
where o(g) = m and o(h) = n. Since we have |G × H| = |G| |H| = mn, it suffices to show that o((g, h)) = nm. We have (g, h)nm = (gnm, hnm) = (1, 1). If (g, h)k = (1, 1), then gk = 1 and hk = 1, so m  k and n
k and n  k. But gcd (n, m) = 1, then implies nm
k. But gcd (n, m) = 1, then implies nm  k (Theorem 5 §1.2)), so o((g, h)) = mn, as required.
k (Theorem 5 §1.2)), so o((g, h)) = mn, as required.
26. a. Write o(gh) = d. Since gh = hg, we have
![]()
This means d  mn. To prove mn
mn. To prove mn  d, it suffices to show m
d, it suffices to show m  d and n
d and n  d (by Theorem 5 §1.2 because gcd (m, n) = 1). This in turn follows if we can show gd = 1 and hd = 1 . We have 1 = (gh)d = gdhd, so gd = h−d
d (by Theorem 5 §1.2 because gcd (m, n) = 1). This in turn follows if we can show gd = 1 and hd = 1 . We have 1 = (gh)d = gdhd, so gd = h−d
 g
g  ∩
∩  h
h  . But
. But 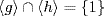 because gcd (m, n) = 1. Thus gd = 1 and h−d = 1, as required. If gcd (m, n) ≠ 1, nothing can be said (for example h = g−1).
because gcd (m, n) = 1. Thus gd = 1 and h−d = 1, as required. If gcd (m, n) ≠ 1, nothing can be said (for example h = g−1).
27. a. If A ⊆ B, then ga B =
B =  gb
gb  , say ga = gbq,
, say ga = gbq, 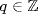 . Since o(g) =∞, a = qb. Conversely, if a = qb, then ga
. Since o(g) =∞, a = qb. Conversely, if a = qb, then ga  B, so A ⊆ B.
B, so A ⊆ B.
29. Write o(gk) = m. Then (gk)n/d = (gn)k/d = 1k/d = 1 implies that m  (n/d). On the other hand, write d = xk + yn with
(n/d). On the other hand, write d = xk + yn with  (by Theorem 3 §1.2). Then (gk)m = 1 implies gdm = (gkm)x · (gn)ym = 1, so n
(by Theorem 3 §1.2). Then (gk)m = 1 implies gdm = (gkm)x · (gn)ym = 1, so n  dm. If qn = dm,
dm. If qn = dm,  , then
, then 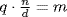 , so (n/d)
, so (n/d)  m. This shows (n/d) = m, as required.
m. This shows (n/d) = m, as required.
31. a. We have a  m and b
m and b  m, so gm
m, so gm  A and gm
A and gm  B. Thus gm
B. Thus gm  A ∩ B, whence
A ∩ B, whence  gm
gm  ⊆ A ∩ B. Conversely, write A∩ B =
⊆ A ∩ B. Conversely, write A∩ B =  gc
gc  . Then gc
. Then gc  A, say gc = (ga)x. Since o(g) =∞, this implies c = ax. Similarly, gc
A, say gc = (ga)x. Since o(g) =∞, this implies c = ax. Similarly, gc  B implies c = by. Thus c is a common multiple of a and b, so m
B implies c = by. Thus c is a common multiple of a and b, so m  c by the definition of the least common multiple. This implies A∩ B =
c by the definition of the least common multiple. This implies A∩ B =  gc
gc  ⊆
⊆  gm
gm  .
.
32. (1) ⇒ (2). Let H and K be subgroups of G = g
g  where o(g) = pn. By Theorem 9, let H =
where o(g) = pn. By Theorem 9, let H = ga
ga  and K =
and K = gb
gb  where a and b are divisors of pn. Since p is a prime, this means a = pl and b = pm. If l ≤ m, this says a
where a and b are divisors of pn. Since p is a prime, this means a = pl and b = pm. If l ≤ m, this says a  b, whence K ⊆ H. The other alternative is m ≤ l, so H ⊆ K.
b, whence K ⊆ H. The other alternative is m ≤ l, so H ⊆ K.
33. If G is cyclic, it is finite (because infinite cyclic groups have infinitely many subgroups). So assume G is not cyclic. Use induction on the number n of distinct subgroups of G. If n = 1, G = {1} is finite. If it holds for n = 1, 2, . . ., k, let H1 = {1}, H2, . . ., Hk, Hk+1 = G be all the subgroups of G. If 1 ≤ i ≤ k then Hi ⊆ G so Hi is finite by induction. So it suffices to show G = H1 ∪ H2 ∪  ∪ Hk. But if g
∪ Hk. But if g  G, then
G, then  g
g  ≠ G because we are assuming that G is not cyclic. Hence
≠ G because we are assuming that G is not cyclic. Hence  g
g  = Hi for some i, so g
= Hi for some i, so g  Hi.
Hi.
35. a. Let 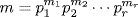 and
and 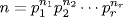 where the pi are distinct primes and mi ≥ 0, ni ≥ 0 for each i. For each i, define xi and yi by
where the pi are distinct primes and mi ≥ 0, ni ≥ 0 for each i. For each i, define xi and yi by
![]()
If 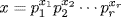 and
and 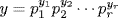 , then x
, then x  m, y
m, y  n and x and y are relatively prime. Thus o(am/x) = x and o(bn/y) = y by Theorem 10, so o(am/x · bn/y) = xy by Exercise 26(a). But xi + yi = max (mi, ny) for each i, so xy = lcm(m, n) by Theorem 9 §1.2.
n and x and y are relatively prime. Thus o(am/x) = x and o(bn/y) = y by Theorem 10, so o(am/x · bn/y) = xy by Exercise 26(a). But xi + yi = max (mi, ny) for each i, so xy = lcm(m, n) by Theorem 9 §1.2.
37. Let cards numbered 1, 2, 3, . . . be initially in position 1, 2, 3, . . . in the deck. Then after a perfect shuffle, position 1 contains card 1, position 2 contains card n + 1, position 3 contains card 2, position 4 contains cards n+ 2, . . .. In general,
![]()
Thus 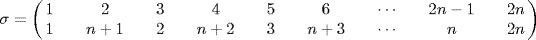 . Note that σ fixes 1 and 2n. The number of shuffles required to regain the initial order is o(σ). Use Example 9.
. Note that σ fixes 1 and 2n. The number of shuffles required to regain the initial order is o(σ). Use Example 9.
a. 

..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
