0.1 Proofs
1.
a.
1. If n = 2k, k an integer, then n2 = (2k)2 = 4k2 is a multiple of 4.
2. The converse is true: If n2 is a multiple of 4 then n must be even because n2 is odd when n is odd (Example 1).
c.
1. Verify: 23 − 6 · 22 + 11 · 2 − 6 = 0 and 33 − 6 · 32 + 11 · 3 − 6 = 0.
2. The converse is false: x = 1 is a counterexample. because
2.
a. Either n = 2k or n = 2k + 1, for some integer k. In the first case n2 = 4k2; in the second n2 = 4(k2 + k) + 1.
c. If n = 3k, then n3 − n = 3(9k3 − k); if n = 3k + 1, then
if n = 3k + 2, then n3 − n = 3(9k3 + 18k2 + 11k + 2).
3.
a.
1. If n is not odd, then n = 2k, k an integer, k ≥ 1, so n is not a prime.
2. The converse is false: n = 9 is a counterexample; it is odd but is not a prime.
c.
1. If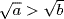 
then 
, that 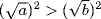is a > b, contrary to the assumption.
then , that is a > b, contrary to the assumption.
2. The converse is true: If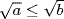 
then 
, that is a ≤ b.
then , that is a ≤ b.
4.
a. If x > 0 and y > 0 assume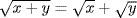 
. Squaring gives 
, whence 
. This means xy = 0 so x = 0 or y = 0, contradicting our assumption.
. Squaring gives 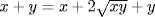, whence 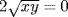. This means xy = 0 so x = 0 or y = 0, contradicting our assumption.
c. Assume all have birthdays in different months. Then there can be at most 12 people, one for each month, contrary to hypothesis.
5.
a. n = 11 is a counterexample because then n2 + n + 11 = 11 · 13 is not prime. Note that n2 + n + 11 is prime if 1 ≤ n ≤ 9 as is readily verified, but n = 10 is also a counterexample as 102 + 10 + 11 = 112.
c. n = 6 is a counterexample because there are then 31 regions. Note that the result holds if 2 ≤ n ≤ 5.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.