8.2 Cauchy's Theorem
1. a. D4 = {1, a, a2, a3, b, ba, ba2, ba3} where o(a) = 4, o(b) = 2 and aba = b. The classes are {1}, {a, a3}, {a2}, {b, ba2}, {ba, ba3}. Since normal subgroups are of orders 1, 2, 4, 8, they are {1}, {1, a2}, {1, a, a2, a3}, {1, b, a2, ba2}, {1, a2, ba, ba3} and D4.
3. If am = g−1ag with g  G, then
G, then
![]()
By induction we get 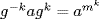 for all k ≥ 0. Since G is finite, let gk = 1, k ≥ 1. Then
for all k ≥ 0. Since G is finite, let gk = 1, k ≥ 1. Then 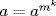 whence 1 − mk = qn. This gives 1 = mk + qn, so gcd (m, n) = 1.
whence 1 − mk = qn. This gives 1 = mk + qn, so gcd (m, n) = 1.
5. Let H = class a1 ∪ . . . ∪ classan. Given g  G and h
G and h  H, let h
H, let h  classai. Then g−1hg
classai. Then g−1hg  classai ⊆ H, so g−1hg
classai ⊆ H, so g−1hg  H. Then g−1Hg ⊆ H, as required.
H. Then g−1Hg ⊆ H, as required.
7. Let K = g−1Hg, so H = gKg−1. We claim N(K) = g−1N(H)g. Let a  N(K) so a−1Ka = K. To show a
N(K) so a−1Ka = K. To show a  g−1N(H)g it suffices to show gag−1
g−1N(H)g it suffices to show gag−1  N(H). But
N(H). But
![]()
as required. Hence N(K) ⊆ g−1N(H)g. Similarly N(H) ⊆ gN(K)g−1 so g−1N(H)g ⊆ N(K).
9. If |class a| = 2 then |G : N(a)| = 2 by Theorem 2. Hence N(a) is normal in G. Since N(a) ≠ G we are done if N(a) ≠ {1}. But N(a) = {1} implies |G| = |G : N(a)| = 2 so G is abelian and every conjugacy class is a singleton, a contradiction.
11. We have H ⊆ N(H) ⊆ G and H has finite index m in G. So
![]()
by Exercise 31 §2.6. Thus |G : N(H)| is finite, and H has |G : N(H)| conjugates by Theorem 2.
13. Write X = {g−1Hg  g
g  G} and Y = {N(H)g
G} and Y = {N(H)g  g
g  G}. Define ϕ : X → Y by ϕ(g−1Hg) = N(H)g. Then:
G}. Define ϕ : X → Y by ϕ(g−1Hg) = N(H)g. Then:
![]()
Thus ϕ is well defined and one-to-one; it is clearly onto.
15. Let α = γ1γ2. . . γr in Sn where the γi are disjoint cycles. Given σ  Sn,
Sn,
![]()
and this is the factorization of σ−1ασ into disjoint cycles by Lemma 3 §2.8. Since γi and σ−1γiσ have the same length, σ−1ασ has the same cycle structure as σ. Conversely let α and β have the same cycle structure, say
![]()
where the γi (the δi) are disjoint cycles, and γi and δi have equal length for each i. If γi = (ki1, ki2, . . ., kis) and δi = (li1li2. . . lis) for all i define σ  Sn by
Sn by
![]()
Then σ is a permutation and σ−1γiσ = δi by Lemma 3 §2.8. Hence σ−1ασ = β, that is α and β are conjugate.
17. a. S4 consists of ε, three permutations of type (a b)(c d), eight 3-cycles, six 2-cycles and six 4-cycles. These are the conjugacy classes by Exercise 15. So, by Theorem 1, each normal subgroup H  S4 is a union of these classes. Since |H| divides 24 = |S4|, and since ε
S4 is a union of these classes. Since |H| divides 24 = |S4|, and since ε  H, the only possibilities are H = ε, H = K, H = A4 and H = S4.
H, the only possibilities are H = ε, H = K, H = A4 and H = S4.
19. It suffices to show that G is abelian (then there are |G| conjugacy classes). So assume G is not abelian. Then there must be a nonsingleton conjugacy class, say class a. Thus there is only one singleton class, {1}. This means |G| = 1 + |class a| = 1 + |G : N(a)|. Write m = |G : N(a)| so that |G| = md, d ≥ 2. But then md = 1 + m gives 1 = m(d − 1) so m = 1, that is |class a| = 1, contrary to assumption.
21. If G/K and K are p-groups, let g  G. Then
G. Then 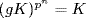 in G/K for some n, so
in G/K for some n, so 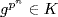 . Since K is itself a p-group,
. Since K is itself a p-group, 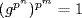 for some m; that is
for some m; that is  . Thus o(g) is a power of p, so G is a p-group. Conversely, subgroups of p-groups are clearly p-groups, as are images because if
. Thus o(g) is a power of p, so G is a p-group. Conversely, subgroups of p-groups are clearly p-groups, as are images because if  then
then 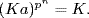
23. We have |G| = pn for some n ≥ 1 so 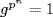 for all g
for all g  G. It follows that
G. It follows that 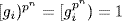 in
in 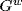 for all [gi) in
for all [gi) in 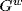 , so
, so 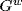 is a p-group. If 1 ≠ g and 1 ≠ h then [g, 1, 1, . . .), [1, g, 1, 1, . . .), . . . are all distinct in
is a p-group. If 1 ≠ g and 1 ≠ h then [g, 1, 1, . . .), [1, g, 1, 1, . . .), . . . are all distinct in 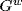 . So
. So 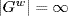 .
.
25. By Theorem 1, H is a union of G-conjugacy classes; suppose there are m of these which are singletons. The remaining classes in H have order a multiple of p by Theorem 3 (since G is a p-group) and p divides |H| (since H ≠ {1}). Hence p|m. Since m > 0 (because {1} ⊆ H) this means m > 1 and there exists a ≠ 1, such that class a = {a} ⊆ H. But class a = {a} means a  Z(G), so a
Z(G), so a  H ∩ Z(G).
H ∩ Z(G).
26. a. Let |G| = p3, G nonabelian. Write Z = Z(G). Then Z ≠ {1} by Theorem 6 and Z ≠ G because Gisnonabelian so |Z| = p or p2. If |Z| = p2 then |G/Z| = p so G/Z is cyclic and G is abelian by Theorem 2 §2.9, contrary to assumption. So |Z| = p. Then |G/Z| = p2 so G/Z is abelian by Theorem 8. Hence G′ ⊆ Z so G′ = {1} or G′ = Z. But G′ = {1} implies G is abelian. So G′ = Z. Finally, if K  G, |K| = p, then G/K is abelian so G′ ⊆ K. Thus |K| = p = |Z| = |G′| implies K = G′.
G, |K| = p, then G/K is abelian so G′ ⊆ K. Thus |K| = p = |Z| = |G′| implies K = G′.
27. We proceed by induction on n where |G| = pn. If n = 1 it is clear. In general |H| = pm. If H = {1} it is clear. If H ≠ {1} let K = H ∩ Z(G). Then K  G and K ≠ {1} by Exercise 25. Let |K| = pb. We have H/K
G and K ≠ {1} by Exercise 25. Let |K| = pb. We have H/K  G/K so, by induction, let
G/K so, by induction, let 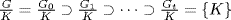 where
where 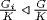 and
and 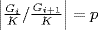 for all i. Thus Gi
for all i. Thus Gi  G and |Gi/Gi+1| = p for all i. Similarly
G and |Gi/Gi+1| = p for all i. Similarly
![]()
where Gi  G for each i and |Gi/Gi+1| = p. These Gi do it.
G for each i and |Gi/Gi+1| = p. These Gi do it.
29. Since C  G, let Z[G/C] = K/C. Since |G/C| > 1, Theorem 6 shows C ⊂ K. But K
G, let Z[G/C] = K/C. Since |G/C| > 1, Theorem 6 shows C ⊂ K. But K  G so K
G so K 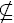 H by Exercise 26 §2.8. If k
H by Exercise 26 §2.8. If k  K then kC is in the center of G/C, so h−1k−1hk
K then kC is in the center of G/C, so h−1k−1hk  C
C  H. Hence k−1Hk ⊆ H, and similarly kHk−1 ⊆ H. Thus k
H. Hence k−1Hk ⊆ H, and similarly kHk−1 ⊆ H. Thus k  N(H) and we have shown K ⊆ N(H).
N(H) and we have shown K ⊆ N(H).
31. The associativity is verified as follows:
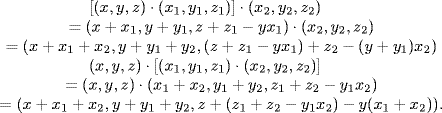
These are equal. The unity is (0, 0, 0) and (x, y, z)−1 = (− x, − y, − z − xy) for all (x, y, z). The group is nonabelian because (1, 1, 0) · (1, 0, 0) = (2, 1, − 1) while (1, 0, 0) · (1, 1, 0) = (2, 1, 0). Finally 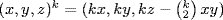 for all k ≥ 2 by induction on k. If k = p,
for all k ≥ 2 by induction on k. If k = p,  . Since
. Since 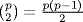 and p is odd, this is (0, 0, 0) so o((x, y, z)) = p.
and p is odd, this is (0, 0, 0) so o((x, y, z)) = p.
33.
a. Given a  G, |class a| = |G : N(a)| by Theorem 2. But
G, |class a| = |G : N(a)| by Theorem 2. But
![]()
so the fact that |G : Z(G)| is finite implies |G : N(a)| is finite.
c. If G = X
X  and a
and a  G, write
G, write 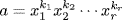 , xi
, xi  X,
X, 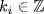 . We claim that
. We claim that 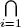 N(xi) ⊆ N(a). For if g
N(xi) ⊆ N(a). For if g  N(xi) for all i then gxi = xig for all i, so ga = ag; that is g
N(xi) for all i then gxi = xig for all i, so ga = ag; that is g  N(a). But each N(xi) has finite index by Theorem 2, so
N(a). But each N(xi) has finite index by Theorem 2, so 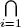 N(xi) has finite index by Poincaré's Theorem [Exercise 33 §2.6], so N(a) has finite index. Thus |class a| is finite.
N(xi) has finite index by Poincaré's Theorem [Exercise 33 §2.6], so N(a) has finite index. Thus |class a| is finite.
e. If a, b  G∗ we have N(a) ∩ N(b) ⊆ N(ab). Since N(a) ∩ N(b) has finite index (Poincaré's theorem), so does N(ab) by the following Lemma. Thus ab
G∗ we have N(a) ∩ N(b) ⊆ N(ab). Since N(a) ∩ N(b) has finite index (Poincaré's theorem), so does N(ab) by the following Lemma. Thus ab  G∗.
G∗.
i. Lemma. If K ⊆ H ⊆ G are groups and |G : K| is finite, then |G : H| is finite. Proof. We have H = ∪ {hK  h
h  H}, a finite union because {gK
H}, a finite union because {gK  g
g  G} is finite. If H = h1K ∪
G} is finite. If H = h1K ∪  ∪ hnK, a disjoint union, then
∪ hnK, a disjoint union, then
![]()
Hence there are at most a finite number of cosets gH.
Next, N(a−1) = {g  ga−1 = a−1g} = {g
ga−1 = a−1g} = {g  ga = ag} = N(a), so a−1
ga = ag} = N(a), so a−1  G∗ too. Clearly 1
G∗ too. Clearly 1  G∗, so G∗ is a subgroup. Finally, G∗ is itself an FC-group. Indeed, if a
G∗, so G∗ is a subgroup. Finally, G∗ is itself an FC-group. Indeed, if a  G∗
G∗
![]()
Now let σ : G → G be an automorphism. If a  G∗ then
G∗ then
![]()
Since class a is finite, this shows class σ(a) is finite, that is σ(a)  G∗.
G∗.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
