11.2 The Wedderburn-Artin Theorem
1. The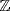 
-modules are the (additive) abelian groups, so the simple ones are the simple abelian groups. These are the prime cycles 
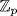(in additive notation) where p is a prime. Hence the semisimple 
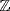-modules are the the direct sums of copies of these 
for various primes p. The homogeneous semisimple 
-modules are the direct sums of copies of 
for a fixed prime p.
-modules are the (additive) abelian groups, so the simple ones are the simple abelian groups. These are the prime cycles (in additive notation) where p is a prime. Hence the semisimple -modules are the the direct sums of copies of these for various primes p. The homogeneous semisimple 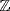-modules are the direct sums of copies of 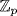for a fixed prime p.
2. a. Since RR is complemented by Theorem 1, we have R = L ⊕ M for some left ideal M. Write 1 = e + f where e 
L and f M. Hence Re ⊆ L, and we claim this is equality. If x L then x − xe = xf L ∩ M = 0 because x − xe L and xf M. Hence x = xe Re, so L ⊆ Re, as required.
L and f M. Hence Re ⊆ L, and we claim this is equality. If x L then x − xe = xf L ∩ M = 0 because x − xe L and xf M. Hence x = xe Re, so L ⊆ Re, as required.
3. a. Let α, β E. Then (α + β) · x = (α + β)(x) = α(x) + β(x) = α · x + β · x so Axiom M2 holds (see Section 11.1). Similarly,
E. Then (α + β) · x = (α + β)(x) = α(x) + β(x) = α · x + β · x so Axiom M2 holds (see Section 11.1). Similarly,
proves Axiom M3. The other axioms are routinely verified.
5. Let N1, N2, . . ., Nm be maximal submodules of M. Define
by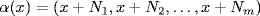 
for all x M. Then α is R-linear and ker(α) = {x M 
x + Ni = 0 for each i} = ∩ iNi. Since each 
is simple, M/(∩ iNi) ≅ α(M) is semisimple by Corollary 1 of Theorem 2.
for all x M. Then α is R-linear and ker(α) = {x M x + Ni = 0 for each i} = ∩ iNi. Since each 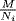is simple, M/(∩ iNi) ≅ α(M) is semisimple by Corollary 1 of Theorem 2.
7. If M is a finitely generated semisimple module then (Lemma 4) M is a finite direct sum of simple submodules. By Theorem 2 M = H1 ⊕ 
⊕ Hn where the Hi are the homogeneous components of M. By the preceding exercise, end(M) ≅ end(H1) × × end(Hn), so it suffices to show that end(H) is semisimple for any finitely generated, homogeneous, semisimple module H. But then H is a finite direct sum of isomorphic simple modules (using Lemma 4), and so H ≅ Kn for some simple module K. Now Lemma 3 §11.1 gives end(H) ≅ Mn(end K) . Since end K is a division ring by Schur's lemma, we are done.
⊕ Hn where the Hi are the homogeneous components of M. By the preceding exercise, end(M) ≅ end(H1) × × end(Hn), so it suffices to show that end(H) is semisimple for any finitely generated, homogeneous, semisimple module H. But then H is a finite direct sum of isomorphic simple modules (using Lemma 4), and so H ≅ Kn for some simple module K. Now Lemma 3 §11.1 gives end(H) ≅ Mn(end K) . Since end K is a division ring by Schur's lemma, we are done.
9. Let K be a simple left ideal of R. If R is a domain and then K2 ≠ 0 so Brauer's lemma shows that K = Re where e2 = e. But e(1 − e) = 0 so, again since R is a domain, e = 0 or e = 1 . Since K ≠ 0 we must have e = 1, whence R = Re is simple as a left R-module. But then, given 0 ≠ a R, we have Ra = R, say ba = 1 . Again, b ≠ 0 so Rb = R, say cb = 1 . Now compute:
R, we have Ra = R, say ba = 1 . Again, b ≠ 0 so Rb = R, say cb = 1 . Now compute:
Hence ab = cb = 1 and we have proved that a is a unit with inverse b. Since a ≠ 0 was arbitrary, this shows that R is a division ring.
11. If A is an ideal of R, we must show that every left ideal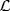 
of the ring R/A is semisimple as an R/A-module. But 
is an R-submodule of the left R-module R/A because (r + A)(s + A) = rs + A = r(s + A) . Hence 
is semisimple as a left R -module by Corollary 1 of Theorem 1 (since RR is semisimple). Since the R-action and the R/A-action on 
are the same, it follows that 
is semisimple as a left R/A-submodule. This is what we wanted.
of the ring R/A is semisimple as an R/A-module. But 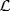is an R-submodule of the left R-module R/A because (r + A)(s + A) = rs + A = r(s + A) . Hence 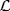is semisimple as a left R -module by Corollary 1 of Theorem 1 (since RR is semisimple). Since the R-action and the R/A-action on 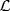are the same, it follows that 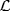is semisimple as a left R/A-submodule. This is what we wanted.
13. (2) ⇒ (1). Assume that eRe is a division ring, and that R is semiprime. Choose 0≠ x Re ; we must show that Rx = Re, that is e Rx. Since R is semiprime we have xRx ≠ 0, say xax ≠ 0, a R. Since x Re, we have xe = x, so xe(ax) ≠ 0 . This means eax ≠ 0 so eaxe ≠ 0 (again since x = xe) . As eRe is a division ring, there exists t eRe such that t(eax) = e. Thus e Rx, as required.
Re ; we must show that Rx = Re, that is e Rx. Since R is semiprime we have xRx ≠ 0, say xax ≠ 0, a R. Since x Re, we have xe = x, so xe(ax) ≠ 0 . This means eax ≠ 0 so eaxe ≠ 0 (again since x = xe) . As eRe is a division ring, there exists t eRe such that t(eax) = e. Thus e Rx, as required.
15. Let RR be semisimple. Then Lemma 4 implies that R = K1 ⊕ K2 ⊕ ⊕ Kn where the Ki are simple left ideals. Hence R is left noetherian by the Corollary to Lemma 2 §11.1. Since RR is also semisimple by Theorem 5, the same argument shows that R is right noetherian. [Note that this also shows that R is left and right artinian.]
⊕ Kn where the Ki are simple left ideals. Hence R is left noetherian by the Corollary to Lemma 2 §11.1. Since RR is also semisimple by Theorem 5, the same argument shows that R is right noetherian. [Note that this also shows that R is left and right artinian.]
16. Let R be a semiprime ring.
a. If LM = 0 where L and M are left ideals, then
Since ML is a left ideal and R is semiprime, this gives ML = 0.
c. If rA = 0 then (Ar)2 = ArAr = A0r = 0, Hence Ar = 0 because Ar is a left ideal and R is semiprime. The converse is similar.
17. Write R = R1 × R2 × × Rn. By Exercise 4, every ideal A of has the form A = A1 × A2 × × An where each Ai an ideal of Ri. Hence A2 = 0 if and only if 
for each i. The result follows.
× Rn. By Exercise 4, every ideal A of has the form A = A1 × A2 × × An where each Ai an ideal of Ri. Hence A2 = 0 if and only if 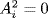for each i. The result follows.
19. If R is semiprime, let 
be an ideal of Mn(R) . By Lemma 3 §3.3, 
has the form 
for some ideal A of R. Hence if 
then A2 = 0, whence A = 0, so 
This shows that Mn(R) is semiprime for any n ≥ 1 . Conversely, assume that Mk(R) is semiprime for some k. If A2 = 0 where A is an ideal of R, then Mk(A) is an ideal of Mk(R) and Mk(A)2 = 0 . Hence Mk(A) = 0, whence A = 0 . This shows that R is semiprime.
be an ideal of Mn(R) . By Lemma 3 §3.3, 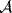has the form 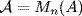for some ideal A of R. Hence if then A2 = 0, whence A = 0, so 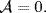This shows that Mn(R) is semiprime for any n ≥ 1 . Conversely, assume that Mk(R) is semiprime for some k. If A2 = 0 where A is an ideal of R, then Mk(A) is an ideal of Mk(R) and Mk(A)2 = 0 . Hence Mk(A) = 0, whence A = 0 . This shows that R is semiprime.
20. a. If ab = 0 in R then (Ra)(Rb) = 0 because R is commutative. Hence, if R is prime either Ra = 0 or Rb = 0, that is a = 0 or b = 0 . Thus R is a domain. Conversely, if R is a domain and AB = 0 then, if A ≠ 0 ≠ B, choose 0 ≠ a A and 0 ≠ b B. Then ab AB = 0, a contradiction. So either A = 0 or B = 0 ; that is R is a prime ring.
A and 0 ≠ b B. Then ab AB = 0, a contradiction. So either A = 0 or B = 0 ; that is R is a prime ring.
21. Write P = P1 ⊕ P2 ⊕ ⊕ Pn, and view P as an internal direct sum. Then each Pi is isomorphic to a direct summand of a free module Fi ; by Lemma 9 we may assume that Fi = Pi ⊕ Qi. Then F = F1 ⊕ F2 ⊕ ⊕ Fn is also free, and F = (P1 ⊕ P2 ⊕ ⊕ Pn) ⊕ (Q1 ⊕ Q2 ⊕ ⊕ Qn) . Hence P1 ⊕ P2 ⊕ ⊕ Pn is projective by Theorem 3.
⊕ Pn, and view P as an internal direct sum. Then each Pi is isomorphic to a direct summand of a free module Fi ; by Lemma 9 we may assume that Fi = Pi ⊕ Qi. Then F = F1 ⊕ F2 ⊕ ⊕ Fn is also free, and F = (P1 ⊕ P2 ⊕ ⊕ Pn) ⊕ (Q1 ⊕ Q2 ⊕ ⊕ Qn) . Hence P1 ⊕ P2 ⊕ ⊕ Pn is projective by Theorem 3.
22.
a. If α : M → N is R-linear and K ⊆ M is simple then either α(K) = 0 or γ(K) ≅ K by Schur's lemma. Either way, α(K) ⊆ soc N. Since soc M is a sum of simple submodules of M, it follows that α(soc M) ⊆ soc N.
c. If M = N1 ⊕ N1 it is clear that soc(N1)⊕ soc(N2) ⊆ soc M because soc(Ni) is semisimple for each i. For the other inclusion, define the projection π1 : M → N1 by π1(n1 + n2) = n1, and define π2 : M → N2 analogously. If K ⊆ M is any simple module then πi(K) ⊆ socNi for each i [πi(K) is either 0 or isomorphic to K by Schur's lemma]. Hence if k K then k = π1(k)+ π2(k) soc(Ni)⊕ soc(Ni) . It follows that
K then k = π1(k)+ π2(k) soc(Ni)⊕ soc(Ni) . It follows that
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.