0.3 Mappings
1.
a. Not a mapping: α(1) = − 1 is not in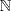 
.
.
c. Not a mapping: 
is not in 
.
is not in .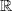
e. Not a mapping: α(6) = α(2 · 3) = (2, 3) and α(6) = α(1 · 6) = (1, 6).
g. Not a mapping: α(2) is not defined.
2.
a. Bijective. α(x) = α(x1) implies 3 − 4x = 3 − 4x1, so x = x1, and α is one-to-one. Given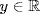 
, 
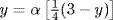, so α is onto.
, , so α is onto.
c. Onto: If m 
N, then m = α(2m − 1) = α(2m). Not one-to-one: In fact we have α(1) = 1 = α(2).
N, then m = α(2m − 1) = α(2m). Not one-to-one: In fact we have α(1) = 1 = α(2).
e. One-to-one: α(x) = α(x1) implies (x + 1, x − 1) = (x1 + 1, x1 − 1), whence x = x1. Not onto: (0, 0) ≠ α(x) for any x because (0, 0) = (x + 1, x − 1) would give x = 1 and x = − 1.
g. One-to-one: α(a) = α(a1) implies (a, b0) = (a1, b0) implies a = a1. Not onto if |B| ≥ 2 since no element (a, b) is in α(A) for b ≠ b0.
3.
a. Given c C, let c = βα(a) with a A (because βα is onto). Hence c = β(α(a)), where α(a) B, so β is onto.
C, let c = βα(a) with a A (because βα is onto). Hence c = β(α(a)), where α(a) B, so β is onto.
c. Let β(b) = β(b1). Write b = α(a) and b1 = α(a1) (since α is onto). Then
so a = a1 (because βα is one-to-one), and hence b = b1 as required.
e. Let b B. As α is onto, let b = α(a), a A. Hence
B. As α is onto, let b = α(a), a A. Hence
Since b B was arbitrary, this shows that β = β1.
B was arbitrary, this shows that β = β1.
5.
a. If α2 = α, let x α(A), say x = α(a). Then α(x) = α2(a) = α(a) = x. Conversely, let α(x) = x for all x α(A). If a A, write α(a) = x. Then α2(a) = α(α(a)) = α(x) = x = α(a), so α2 = α.
α(A), say x = α(a). Then α(x) = α2(a) = α(a) = x. Conversely, let α(x) = x for all x α(A). If a A, write α(a) = x. Then α2(a) = α(α(a)) = α(x) = x = α(a), so α2 = α.
c. α2 = (βγ)(βγ) = β(γβ)γ = β(1A)γ = βγ = α.
7.
a. If 
write α−1(y) = x. Hence y = α(x), that is y = ax + b. Solving for x gives 
As this is possible for all 
this shows that 
for all 
.
write α−1(y) = x. Hence y = α(x), that is y = ax + b. Solving for x gives 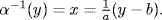As this is possible for all 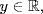this shows that 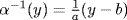for all .
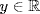c. First verify that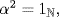 
that is 
Hence α−1 = α by the definition of the inverse of a function.
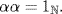that is Hence α−1 = α by the definition of the inverse of a function.
9. Let βα = 1A. Then α is one-to-one because α(a) = α(a1) implies that a = βα(a) = βα(a1) = a1 ; and β is onto because if a A then a = βα(a) = β(α(a)) and α(a) B. Hence both are bijections as |A| = |B| (Theorem 2), and hence α−1 and β−1 exist. But then β−1 = β−11A = β−1(βα) = α. Similarly α−1 = β.
A then a = βα(a) = β(α(a)) and α(a) B. Hence both are bijections as |A| = |B| (Theorem 2), and hence α−1 and β−1 exist. But then β−1 = β−11A = β−1(βα) = α. Similarly α−1 = β.
11. Let ϕ(α) = ϕ(α1) where α and α1 are in M. Then (α(1), α(2)) = (α1(1), α1(2)), so α(1) = α1(1) and α(2) = α1(2). Thus α = α1 (by Theorem 1), so ϕ is one-to-one. Conversely, let (x, y) B × B, and define α2 : {1, 2} → B by α2(1) = x and α2(2) = y. Then α2 M, and ϕ(β) = (α2(1), α2(2)) = (x, y). Thus ϕ is onto. Then ϕ−1 : B × B → M has action ϕ−1(x, y) = α2 where α2(1) = x and α2(2) = y.
B × B, and define α2 : {1, 2} → B by α2(1) = x and α2(2) = y. Then α2 M, and ϕ(β) = (α2(1), α2(2)) = (x, y). Thus ϕ is onto. Then ϕ−1 : B × B → M has action ϕ−1(x, y) = α2 where α2(1) = x and α2(2) = y.
13. For each a A there are m choices for α(a) B. Since |A| = n, there are mn choices in all, and they all lead to different functions α because α is determined by these choices.
A there are m choices for α(a) B. Since |A| = n, there are mn choices in all, and they all lead to different functions α because α is determined by these choices.
15.
a.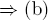 
Given b B, write Ab = {a A 
α(a) = b}. Then Ab≠ for each b (α is onto), so choose ab Ab for each b B. Then define β : B → A by β(b) = ab. Then αβ(a) = α(β(b)) = α(ab) = b for each b; that is αβ = 1B.
Given b B, write Ab = {a A α(a) = b}. Then Ab≠ for each b (α is onto), so choose ab Ab for each b B. Then define β : B → A by β(b) = ab. Then αβ(a) = α(β(b)) = α(ab) = b for each b; that is αβ = 1B.
c.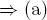 
If b0 B − α(A), we deduce a contradiction. Choose a0 A, and define β : B → B by:
If b0 B − α(A), we deduce a contradiction. Choose a0 A, and define β : B → B by:
Then α(a) ≠ b0 for all a A, so
A, so
for all a A. Hence, βα = 1Bα, so β = 1B by (c). Finally then b0 = β(b0) = α(a0), a contradiction.
A. Hence, βα = 1Bα, so β = 1B by (c). Finally then b0 = β(b0) = α(a0), a contradiction.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.