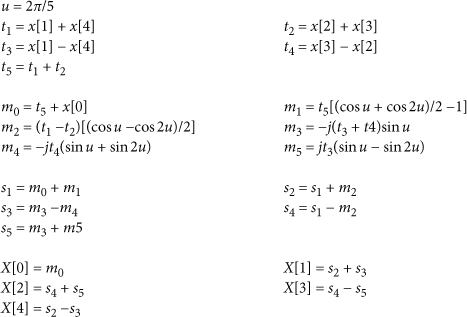Note 19. FFT: Prime Factor Algorithm

The radix-2 algorithms described in Notes 17 and 18 are very useful, but in certain situations, a DFT block size of 2^k is just not acceptable. The prime factor algorithm (PFA) is a technique for constructing fast transforms of length N, where N can be expressed as a product of mutually prime factors. A DFT of length N = N₁N₂ can be restructured as an N₁ by N₂ two-dimensional DFT:

19.1

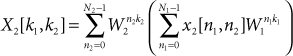
where

W₁ = exp(–j2p/N₁)

W₂ = exp(–j2p/N₂)

In order to make use of the restructured transform, the one-dimensional input sequence, x[n], must be mapped into a two-dimensional sequence, x₂[n₁, n₂], using the index transformation

n ≡ (N₁n₁ + N₂n₁) modulo 2

where

n₁ = 0, 1,    ,N₁ –1

n₁ = 0, 1,    ,N₂ –1

After transformation, the two-dimensional result, X₂[k₁, k₂], is mapped into the one-dimensional result using the index transformation

k ≡ (N₁t₁k₂ + N₂t₂k₁) mogulo 2

where t₁ and t₂ are chosen such that

N₁t₁ = 1 modulo N₂

N₂t₂ = 1 modulo N₁

19.1. Small-N Transforms

There are a number of very efficient specialized implementations for N-point DFTs when N is very small (see Math Boxes 19.1 through 19.3). These implememetations are ideally suited for use as component DFTs in the prime factor algorithm.