Note 16. Exploring DFT Resolution
This note provides demonstrations of a technique called zero padding, which is often used to obtain a finer frequency-domain increment when using a discrete Fourier transform (DFT). These demonstrations show that although zero padding improves the observability of some frequency domain features, it does not improve the frequency resolution of a DFT.
Sometimes important features of a signal’s spectrum fall at frequencies between the DFT bin frequencies, making potentially important features of a signal’s spectrum difficult to detect or observe. This inability to see critical details that fall at frequencies that are not integer multiples of F = NT – 1 is sometimes called the picket fence effect because it is similar to trying to view the details of a scene while looking through a picket fence—some details are clearly visible, while others are hidden by the slats of the fence. The picket fence effect can be mitigated to some extent by reducing the size of the frequency increment, F, but the effect can never be completely eliminated as long as we continue to operate in the discrete frequency domain.
In a DFT, the relationship FNT = 1 always holds. Therefore, the only way that F can be reduced is by increasing T or N. In the design of most signal processing strategies, there is usually not much “wiggle room” when it comes to increasing the value of T. Any viable approach for reducing F must therefore involve increasing N.
16.1. Zero Padding
A classic approach used for decreasing F is called zero padding. This technique involves padding the original N-point input sequence with p zero-valued samples to create an input sequence of length L = N + p. The straightforward approach is to simply extend the DFT to some longer length, L, and collect this new larger number of input samples before computing the L-length DFT.
Example 16.1. Zero Padding Improves Observability
The signal of interest (SOI) is a sinusoid having a frequency of fc = 0.140625 Hz. For the case of T = 1 and N = 32, the sinusoid’s frequency can be expressed in terms of F as fc = 4.5F.
• The positive-frequency half of a 32-point DFT magnitude spectrum for the SOI is shown in Figure 16.1, along with the corresponding DTFT magnitude spectrum.1 The peak in the DTFT occurs at fc = 4.5F, but the DFT provides outputs only at integer multiples of F, making it impossible to observe the peak directly in the DFT result.
Figure 16.1. Fourier spectra from Example 16.1. The spectra are for a rectangularly windowed segment of a sinusoid having a frequency of fc = 4.5F. The solid trace represents the magnitude of the 32-point DTFT, and the dots indicate the magnitude produced by a 32-point DFT.
• Note that the result in Figure 16.1 runs contrary to intuition, which expects the responses at f = 4F and f = 5F to be equal if the signal’s true frequency lies exactly halfway in between 4F and 5F. This observed asymmetry is because the sum of the Dirichlet kernels for f = fc and for f = –fc are not symmetric about fc.
• In an attempt to better observe the frequency of the spectral peak, we increase the DFT length from N = 32 to L = 64 by appending 32 zero-valued samples to the original input sequence. The frequency increment is halved (F′ = F/2), and the frequency corresponding to bin 9 in the new, longer DFT exactly equals the frequency of the sinusoid:
16.1
As shown in Figure 16.2, the result for bin 9 is a peak, but the amplitude of this peak does not match the peak amplitude of the DTFT result, which is plotted for comparison. In fact, none of the 64-point DFT bins appear to be samples of the DTFT result. The DTFT plotted in the figure is the DTFT for a 64-sample segment of the SOI. However, the 64-point DFT results do agree with the DTFT for a 32-sample segment of the SOI, as shown in Figure 16.2. This observation should not come as a surprise; the segment of SOI is only 32 samples long whether zero-padding is employed or not.
Figure 16.2. Fourier spectra from Example 16.1. The spectra are for a rectangularly windowed segment of a sinusoid having a frequency of fc = 4.5F. The dots indicate the magnitudes produced by a 64-point DFT of a 32-sample signal segment that has been padded with 32 zero-valued samples. The solid trace represents the magnitude of the DTFT for a 64-point segment of the original sinusoid.
Zero padding does improve observability of some spectrum features, but contrary to claims often made in the DSP literature, zero padding does not improve frequency resolution in the frequency domain.
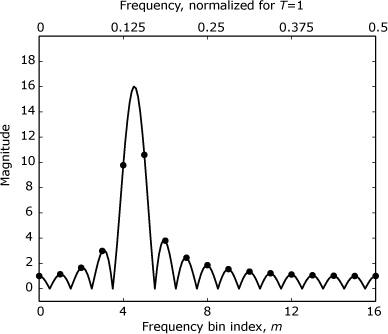
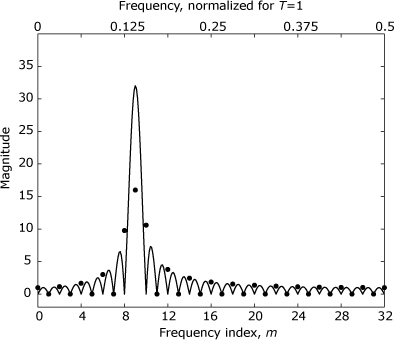
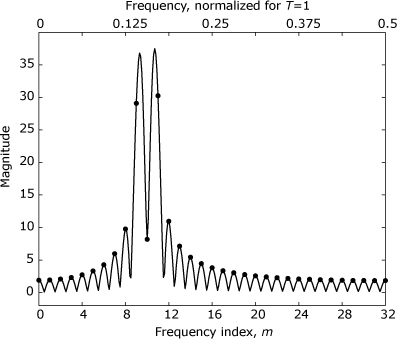
Figure 16.3. Fourier spectra from Example 16.1. The spectra are for a rectangularly windowed segment of a sinusoid having a frequency of fc = 4.5F. The dots indicate the magnitudes produced by a 64-point DFT of a 32-sample signal segment that has been padded with 32 zero-valued samples. The solid trace represents the magnitude of the DTFT for a 32-point segment of the original sinusoid.
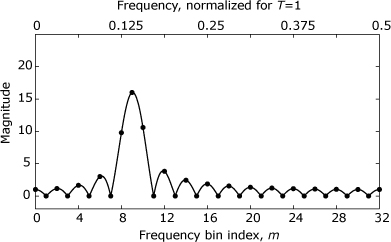
As already stated, the zero padding technique involves extending the original N-point input sequence by appending p zero-valued samples to create an input sequence of length L = N + p. An L-point DFT is then computed instead of an N-point DFT. The frequency domain values then fall at integer multiples of F′ = (LT)–1 rather than at multiples of F = (NT)–1. Because L > N, the new frequency increment of F′ is finer than the original increment of F, thereby improving observability, as demonstrated in Example 16.1.
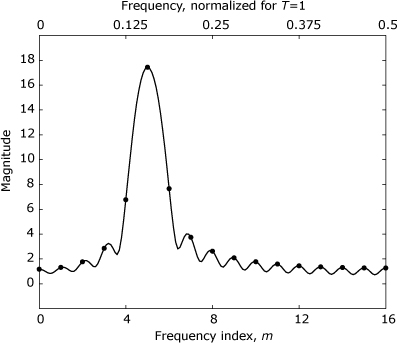
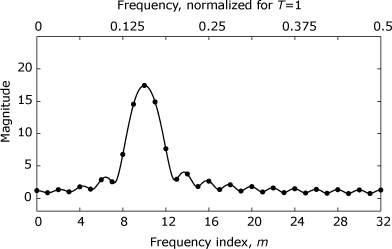
Because zero padding is able to provide improved observability in the discrete-frequency domain, some texts incorrectly claim that zero padding increases the resolution of the DFT. Resolution is the ability to distinguish two closely spaced features in a signal’s spectrum. As shown in Example 16.2, zero padding does not improve the DFT’s resolution.
Example 16.2. Zero Padding Does Not Improve Resolution
The signal of interest (SOI) is the sum of two sinusoids—one having a frequency of f1 = 0.146875 Hz and the other having a frequency of f2 = 0.165625 Hz. For the case of T = 1 and N = 32, the sinusoids’ frequencies can be expressed in terms of F as f1 = 4.7F and f2 = 5.3F.
• The positive-frequency half of a 32-point DFT magnitude spectrum for the SOI is shown in Figure 16.4, along with the corresponding DTFT magnitude spectrum. There is a peak in both the DTFT response and in the DFT response at f = 5F, which is midway between 4.7F and 5.3F. We are not able to distinguish the two different frequency components in this result.
Figure 16.4. Fourier spectra from Examples 16.2 and 16.3. The spectra are for a rectangularly windowed segment of a signal consisting of two sinusoids having frequencies of f1 = 0.146875 = 4.7F and f2 = 0.165625 = 5.3F. The solid trace represents the magnitude of the 32-point DTFT, and the dots indicate the magnitudes produced by a 32-point DFT.
• In an attempt to improve the resolution of the results, we increase the DFT length from N = 32 to L = 64 by appending 32 zero-valued samples to the original input sequence. As shown in Figure 16.5, the DFT result still consists of samples from the DTFT for a 32-sample segment of the SOI. All that zero padding has been able to accomplish is to cause the DFT bins to be more closely spaced in frequency.
Figure 16.5. Fourier spectra from Example 16.2. The spectra are for a rectangularly windowed segment of a signal consisting of two sinusoids having frequencies of f1 = 0.146875 = 4.7F and f2 = 0.165625 = 5.3F. The solid trace represents the magnitude of the DTFT for a 32-sample segment of the signal. The dots indicate the magnitudes produced by a 64-point DFT of a 32-point segment of the signal padded with 32 zero-valued samples.
16.2. Lengthening the DFT
The straightforward approach to improving both observability and resolution in the DFT result is simply to extend the DFT to some longer length, L, and collect this new, larger number of input samples before computing the DFT. Example 16.3 applies this approach to the two-tone signal from Example 16.2.
Example 16.3. Lengthening the DFT Improves Resolution
The signal of interest (SOI) is the sum of two sinusoids—one having a frequency of f1 = 0.146875 Hz and the other having a frequency of f2 = 0.165625. For the case of T = 1 and N = 32, the sinusoids’ frequencies can be expressed in terms of F as f1 = 4.7F and f2 = 5.3F.
• The positive-frequency half of a 32-point DFT magnitude spectrum for the SOI is shown in Figure 16.4, along with the corresponding DTFT magnitude spectrum. There is a peak in both the DTFT response and in the DFT response at f = 5F, which is midway between 4.7F and 5.3F. We are not able to distinguish the two different frequency components in this result.
• In an attempt to improve the resolution of the results, we increase the DFT length from N = 32 to L = 64, and using 64 samples of the SOI, compute the magnitude response shown in Figure 16.6. The DFT result shows two distinct peaks at bins 9 and 11, with a notch between the peaks at bin 10.
Figure 16.6. Fourier spectra from Example 16.3. Spectra are for a rectangularly windowed segment of a signal consisting of two sinusoids having frequencies of f1 = 0.146875 = 4.7F and f2 = 0.165625 = 5.3F. The solid trace represents the magnitude of the DTFT for a 64-sample segment of the SOI, and the dots indicate the magnitudes produced by a 64-point DFT.
