3.3 Ideals and Factor Rings
1.
a. No. 1  A, A ≠ R.
A, A ≠ R.
c. Yes. 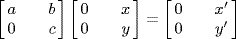 ,
, 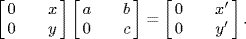
e. No. 1  A.
A.
3.
a. (1 + A)(r + A) = (1 · r + A) = r + A and (r + A)(1 + A) = (r · 1 + A) = r + A.
c. If R is commutative then, for all r + A, s + A in R/A :
![]()
4.
a. mr + ms = m(r + s)  mR, −(mr) = m(− r)
mR, −(mr) = m(− r)  mR; s(mr) = m(sr)
mR; s(mr) = m(sr)  mR; (mr)s = m(rs)
mR; (mr)s = m(rs)  mR. If mr = 0 and mt = 0 then m(r + t) = mr + mt = 0; m(− r) = − mr = 0; m(rs) = (mr)s = 0; and m(sr) = s(mr) = 0 for all s
mR. If mr = 0 and mt = 0 then m(r + t) = mr + mt = 0; m(− r) = − mr = 0; m(rs) = (mr)s = 0; and m(sr) = s(mr) = 0 for all s  R.
R.
5.
a. A × B is clearly an additive subgroup and (r, s)(a, b) = (ra, sb)  A × B for all (r, s)
A × B for all (r, s)  R × S and (a, b)
R × S and (a, b)  A × B. Similarly (a, b)(r, s)
A × B. Similarly (a, b)(r, s)  A × B.
A × B.
c. By (b) let A × B be a maximal ideal of R × S. Then either A = R or B = S (otherwise A × B ⊂ A × S ⊂ R × S). If B = S then A is maximal in R [if A ⊆ B ⊆ R then A × S ⊆ B × S ⊆ R × S so B = A or B = R]. Similarly, if A = R then B is maximal in S. Conversely A × S is maximal in R × S if A is maximal in R, with a similar statement for R × B.
7. Let 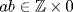 where a = (n, m), b = (k, l). Then
where a = (n, m), b = (k, l). Then 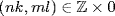 so ml = 0. As
so ml = 0. As 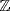 is a domain either m = 0 or n = 0; that is
is a domain either m = 0 or n = 0; that is 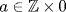 or
or 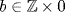 . Hence
. Hence 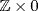 is a prime ideal of
is a prime ideal of 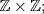 similarly for
similarly for 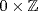 .
.
9.
a. Since i  A = Ri, and since i is a unit in R, A = R. So R/A is the zero ring.
A = Ri, and since i is a unit in R, A = R. So R/A is the zero ring.
c. A = R(1 + 2i). By the Hint 3 + i  A so i + A = − 3 + A. Hence (m + ni) + A = (m − 3n) + A, so each coset in R/A has the form k + A,
A so i + A = − 3 + A. Hence (m + ni) + A = (m − 3n) + A, so each coset in R/A has the form k + A, 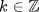 . Moreover, 5 = 2(3 + i) − (1 + 2i)
. Moreover, 5 = 2(3 + i) − (1 + 2i)  A so (as in Example 6)
A so (as in Example 6)
![]()
These are distinct since r + A = s + A, 0 ≤ r ≤ s ≤ 4 means s − r  A, 0 ≤ s − r ≤ 4. Hence s − r = (m + ni)(1 + 2i) for m,
A, 0 ≤ s − r ≤ 4. Hence s − r = (m + ni)(1 + 2i) for m, 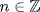 , so taking absolute values, (s − r)2 = (m2 + n2)(12 + 22). Thus 5|(s − r)2 so 5|(s − r). This forces s = r.
, so taking absolute values, (s − r)2 = (m2 + n2)(12 + 22). Thus 5|(s − r)2 so 5|(s − r). This forces s = r.
11.
a. Assume nR ≠ 0 and let A = {r  R
R  nr = 0}. Then A is an ideal of R and A ≠ R because nR ≠ 0. So A = 0.
nr = 0}. Then A is an ideal of R and A ≠ R because nR ≠ 0. So A = 0.
12.
a. If a, b  ann X then (a ± b)x = ax ± bx = 0 and (ra)x = 0 for all r
ann X then (a ± b)x = ax ± bx = 0 and (ra)x = 0 for all r  R.
R.
c. a  ann (X ∪ Y)
ann (X ∪ Y)  at = 0 for all t
at = 0 for all t  X ∪ Y
X ∪ Y  at = 0 for all t
at = 0 for all t  X and at = 0 for all t
X and at = 0 for all t  Y.
Y.
e. By (d) and (b), ann (X) ⊇ ann { ann [ann (X)]}. Let b  ann (X). If y
ann (X). If y  ann [ann (X)] then by = 0. Hence b
ann [ann (X)] then by = 0. Hence b  ann { ann [ann (X)]}.
ann { ann [ann (X)]}.
13. If S is not commutative and C is commutative, then R = S × C is not commutative, but, if A = S × 0, R/A ≅ C is commutative. More interesting example: Let 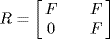 , F a field, and
, F a field, and 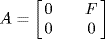 . Then R is not commutative but
. Then R is not commutative but 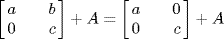 for all
for all  , and
, and 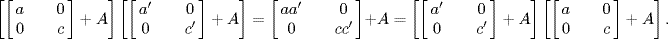 So R/A is commutative.
So R/A is commutative.
14.
a. X + Y is a subgroup because 0 = 0 + 0  X + Y and, if r = x + y and r′ = x′ + y′ are in X + Y then r + r′ = (x + x′) + (y + y′)
X + Y and, if r = x + y and r′ = x′ + y′ are in X + Y then r + r′ = (x + x′) + (y + y′)  X + Y and −r = (− x) + (− y)
X + Y and −r = (− x) + (− y)  X + Y. We have X ⊆ X + Y because x = x + 0
X + Y. We have X ⊆ X + Y because x = x + 0  X + Y for all x
X + Y for all x  X. Similarly Y ⊆ X + Y.
X. Similarly Y ⊆ X + Y.
c. S + A is an additive subgroup because S and A are; and 1 = 1 + 0  S + A. Finally (s + a)(s′ + a′) = ss′ + (sa′ + as′ + aa′)
S + A. Finally (s + a)(s′ + a′) = ss′ + (sa′ + as′ + aa′)  S + A because sa′ + as′ + aa′
S + A because sa′ + as′ + aa′  A.
A.
15. A ∩ S is an additive subgroup since A and S are. If a  A ∩ S and s
A ∩ S and s  S then as
S then as  S (because a
S (because a  S) and as
S) and as  A because A is an ideal of R. Thus as
A because A is an ideal of R. Thus as  S ∩ A, and sa
S ∩ A, and sa  S ∩ A is similar.
S ∩ A is similar.
17.
a. If Z = Z(R) is an ideal then 1  Z forces Z = R, and R is commutative. Conversely, R commutative implies Z = R is an ideal.
Z forces Z = R, and R is commutative. Conversely, R commutative implies Z = R is an ideal.
c. Write Z = Z(R) and let 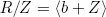 as an additive group. Let r, s
as an additive group. Let r, s  R. Then r + Z = m(b + Z) and s + Z = n(b + Z) where m,
R. Then r + Z = m(b + Z) and s + Z = n(b + Z) where m, 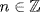 , say r = mb + z and s = nb + z′ where z, z′
, say r = mb + z and s = nb + z′ where z, z′  Z. Hence
Z. Hence
![]()
18.
a. We have 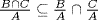 by (3) of Theorem 4. If
by (3) of Theorem 4. If 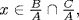 let x = b + A and x = c + A where b
let x = b + A and x = c + A where b  B and c
B and c  C. Hence b + A = c + A, so b − c
C. Hence b + A = c + A, so b − c  A ⊆ C. But then b
A ⊆ C. But then b  c + C = C, so b
c + C = C, so b  B ∩ C. Finally then,
B ∩ C. Finally then,  proving that
proving that 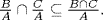
19. A ring S has no nonzero nilpotents if and only if s2 = 0 in S implies s = 0. (Exercise 11 §3.1). If r2  A then (r + A)2 = 0 + A in R/A so r + A = 0 + A, r
A then (r + A)2 = 0 + A in R/A so r + A = 0 + A, r  A. Conversely, if r2
A. Conversely, if r2  A ⇒ r
A ⇒ r  A then (r + A)2 = 0 + A in R/A implies r + A = 0 + A. This shows R/A has no nonzero nilpotents.
A then (r + A)2 = 0 + A in R/A implies r + A = 0 + A. This shows R/A has no nonzero nilpotents.
20.
a. If M is a maximal ideal then R/M is a field, so R/M is an integral domain, so M is prime.
c. No. 0 is a prime ideal of 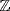 because
because 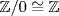 is a domain, but 0 is not maximal because
is a domain, but 0 is not maximal because 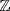 is not a field.
is not a field.
21.
a. (r + A)2 = r2 + A = r + A for all r  R.
R.
c. Given r + A, if rs = 1 = sr then (r + A)(s + A) = 1 + A = (s + A)(r + A). If rn = 0 then (r + A)n = rn + A = 0 + A.
22.
a. Suppose e2 = e in R. Then (e + A)2 = e + A in R/A so e + A = 0 + A or e + A = 1 + A by hypothesis. Thus e  A or 1 − e
A or 1 − e  A. But e
A. But e  A means e is nilpotent (hypothesis) so en = 0, n ≥ 1. But e2 = e ⇒ en = e for all n ≥ 1, so e = 0. If 1 − e
A means e is nilpotent (hypothesis) so en = 0, n ≥ 1. But e2 = e ⇒ en = e for all n ≥ 1, so e = 0. If 1 − e  A then 1 − e = 0 in the same way because (1 − e)2 = 1 − e.
A then 1 − e = 0 in the same way because (1 − e)2 = 1 − e.
c. Suppose the only unit in R/A is 1 + A. If u  R∗ then u + A is a unit in R/A, so u + A = 1 + A by hypothesis. Hence u − 1
R∗ then u + A is a unit in R/A, so u + A = 1 + A by hypothesis. Hence u − 1  A, that is u
A, that is u  1 + A. This shows that R∗⊆ 1 + A ; the other inclusion holds because A consists of nilpotents.
1 + A. This shows that R∗⊆ 1 + A ; the other inclusion holds because A consists of nilpotents.
Conversely, suppose that R∗ = 1 + A. If u + A is a unit in R/A then u  R∗ by (b), so u
R∗ by (b), so u  1 + A by hypothesis. But then u + A = 1 + A. This shows that 1 + A is the only unit in R/A, as required.
1 + A by hypothesis. But then u + A = 1 + A. This shows that 1 + A is the only unit in R/A, as required.
23.
a. 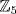 is a field so 0 is the only maximal ideal.
is a field so 0 is the only maximal ideal.
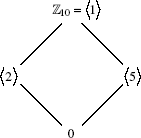
c. The divisors of 10 are 1, 2, 5, 10. So the lattice of additive subgroups is as shown. They are clearly ideals and  2
2 and
and  5
5 are the maximal ones,
are the maximal ones,
25.
a. Since R is commutative, rab = (ra)b  Rb and rab = (rb)a
Rb and rab = (rb)a  Ra for all r
Ra for all r  R.
R.
c. If u is a unit then u  Ru implies Ru = R by Theorem 2. Conversely, if Ru = R then 1
Ru implies Ru = R by Theorem 2. Conversely, if Ru = R then 1  Ru, say 1 = vu,
Ru, say 1 = vu, 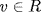 . Hence u is a unit (R is commutative).
. Hence u is a unit (R is commutative).
e. If a = ub, u  R∗, then a
R∗, then a  Rb so Ra ⊆ Rb. But b = u−1a
Rb so Ra ⊆ Rb. But b = u−1a  Ra, so Rb ⊆ Ra too. Conversely, if Ra = Rb then a
Ra, so Rb ⊆ Ra too. Conversely, if Ra = Rb then a  Rb, say a = ub, u
Rb, say a = ub, u  R. Similarly b = va,
R. Similarly b = va, 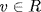 , so a = u(va) = (uv)a. If a = 0 then b = va = 0 so a = 1b. If a ≠ 0 then cancellation (R is a domain) gives 1 = uv.
, so a = u(va) = (uv)a. If a = 0 then b = va = 0 so a = 1b. If a ≠ 0 then cancellation (R is a domain) gives 1 = uv.
26.
a. AB is clearly an additive subgroup and r(∑ i=1aibi) = ∑ i=1(rai)bi  AB for all r. Similarly
AB for all r. Similarly  . Now AB ⊆ A because A is an ideal. Similarly AB ⊆ B, so AB ⊆ A ∩ B.
. Now AB ⊆ A because A is an ideal. Similarly AB ⊆ B, so AB ⊆ A ∩ B.
c. AR ⊆ A because A is an ideal; A ⊆ AR because a = a · 1 for all a  A. Thus A = AR; similarly A = RA.
A. Thus A = AR; similarly A = RA.
27. RaR is clearly an additive subgroup of R, and 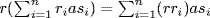 and
and 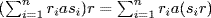 show it is an ideal. Clearly a = 1a1
show it is an ideal. Clearly a = 1a1  RaR. If a
RaR. If a  A, A an ideal, then riasi
A, A an ideal, then riasi  A for all ri, si, so
A for all ri, si, so  . Thus RaR ⊆ A.
. Thus RaR ⊆ A.
29. We have 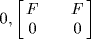 ,
, 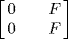 ,
,  and R are all ideals of R. Let A ≠ 0, R be an ideal,
and R are all ideals of R. Let A ≠ 0, R be an ideal,  . If a ≠ 0, b ≠ 0 then
. If a ≠ 0, b ≠ 0 then 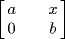 is a unit so A = R. If a = 0, b ≠ 0. Then
is a unit so A = R. If a = 0, b ≠ 0. Then 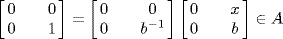 , so
, so 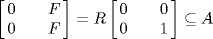 . If
. If 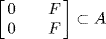 then A contains a unit so A = R. Thus
then A contains a unit so A = R. Thus 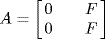 or A = R. Similarly, if
or A = R. Similarly, if  , a ≠ 0, then
, a ≠ 0, then  or A = R. So assume
or A = R. So assume  If
If 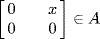 , x ≠ 0, then
, x ≠ 0, then  . So
. So 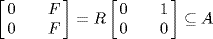 , that is
, that is 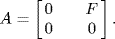
31. Put 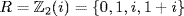 . Then 1, i are units but A = {0, 1, + i} is an ideal because i(1 + i) = 1 + i and (1 + i)(1 + i) = 0. Clearly A ≠ 0 is the only proper ideal.
. Then 1, i are units but A = {0, 1, + i} is an ideal because i(1 + i) = 1 + i and (1 + i)(1 + i) = 0. Clearly A ≠ 0 is the only proper ideal.
32.
a. If 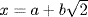 in
in 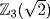 let
let 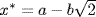 . Then xx∗ = a2 − 2b2 = a2 + b2 in
. Then xx∗ = a2 − 2b2 = a2 + b2 in 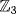 . Now 02 = 0, 12 = 22 = 1, in
. Now 02 = 0, 12 = 22 = 1, in 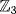 so a2 + b2 ≠ 0 if a ≠ 0 or b ≠ 0. Thus
so a2 + b2 ≠ 0 if a ≠ 0 or b ≠ 0. Thus 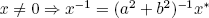 .
.
33.
a. If an = 0 then (ra)n = rnan = 0 for all r. If also bm = 0 consider
![]()
If k ≥ n then an = 0; if n + m − k ≥ m (i.e. k ≤ n) then bn+m−k = 0. So every term in the sum is zero; that is (a + b)n+m = 0. Thus N(R) is an ideal.
c. Let 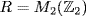 . Then
. Then 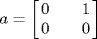 and
and 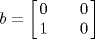 are nilpotent, but
are nilpotent, but  is not
is not 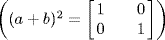 .
.
34.
a. Here J(R) = {0} is an ideal.
c. Write 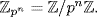 If
If 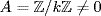 is an ideal of
is an ideal of 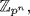 then
then  so k
so k  pn. Hence k = pt for t ≤ n, so A ⊆ M where
pn. Hence k = pt for t ≤ n, so A ⊆ M where 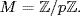 It follows that M is the unique maximal ideal of
It follows that M is the unique maximal ideal of 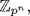 so
so 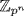 is local and
is local and 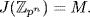
e. Write J = J(R) and J/A = {r + A  r
r  J}. If r + A is a nonunit in R/A then r is a nonunit in R [rs = 1 ⇒ (r + A)(s + A) = 1 + A]. Hence J(R/A) ⊆ J/A. Conversely, let r + A
J}. If r + A is a nonunit in R/A then r is a nonunit in R [rs = 1 ⇒ (r + A)(s + A) = 1 + A]. Hence J(R/A) ⊆ J/A. Conversely, let r + A  J/A, so r
J/A, so r  J. We must show r + A is a nonunit in R/A. Suppose not, and write (r + A)−1 = s + A. Then rs − 1
J. We must show r + A is a nonunit in R/A. Suppose not, and write (r + A)−1 = s + A. Then rs − 1  A so rs − 1
A so rs − 1  J. But r
J. But r  J and J is an ideal, so rs
J and J is an ideal, so rs  J. Thus −1
J. Thus −1  J, 1
J, 1  J, a contradiction.
J, a contradiction.
35.
a. If a, b  M then ab
M then ab  M because ab
M because ab  P ⇒ a
P ⇒ a  P or b
P or b  P (P is prime). Clearly 1
P (P is prime). Clearly 1  M because P ≠ R.
M because P ≠ R.
c. Define 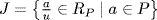 . This is an ideal of RP because
. This is an ideal of RP because 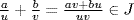 since av + bu + P if a, b
since av + bu + P if a, b  P; and
P; and 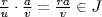 because ra
because ra  P if a
P if a  P. If
P. If 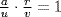 , a
, a  P, then ar = uv so uv
P, then ar = uv so uv  P. P is prime so u
P. P is prime so u  P or
P or 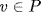 , a contradiction. Thus
, a contradiction. Thus  is a nonunit if a
is a nonunit if a  P so J ⊆ J(RP). Conversely, let
P so J ⊆ J(RP). Conversely, let  . Then we must show r
. Then we must show r  P. But
P. But 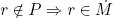 so
so 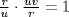 in RP, a contradiction. So r
in RP, a contradiction. So r  P and
P and 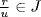 . Hence J = J(RP) so J(RP) is an ideal.
. Hence J = J(RP) so J(RP) is an ideal.
36.
a. We show that J(R) = A. Clearly A ≠ R so A consists of nonunits; that is A ⊆ J(R). Let r  J(R). If r
J(R). If r  A then r + A is a unit in R/A, say (r + A)−1 = s + A. Thus rs − 1
A then r + A is a unit in R/A, say (r + A)−1 = s + A. Thus rs − 1  A, say rs − 1 = a. Hence rs = 1 + a so rs is a unit in R because a is nilpotent by Example 17 §3.1. Similarly sr is a unit in R. If
A, say rs − 1 = a. Hence rs = 1 + a so rs is a unit in R because a is nilpotent by Example 17 §3.1. Similarly sr is a unit in R. If 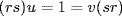 , we see that r is a unit, contrary to r
, we see that r is a unit, contrary to r  J(R).
J(R).
c. The power series for ex is 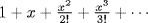 . If a
. If a  A then a is nilpotent so
A then a is nilpotent so 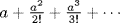 is an element of R which is nilpotent (R is commutative; see Exercise 34(a)). Thus σ : A → 1 + A given by
is an element of R which is nilpotent (R is commutative; see Exercise 34(a)). Thus σ : A → 1 + A given by 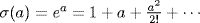 is a map. Similarly
is a map. Similarly 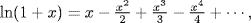 so if a
so if a  A,
A,  . Thus τ : 1 + A → A is well defined by τ(u) = ln u. Now τσ(a) = ln [ea] = a and στ(u) = elnu = u hold, so σ and τ are inverses. Hence σ is a bijection. Finally σ(a + b) = ea+b = eaeb = σ(a)σ(b) for ab
. Thus τ : 1 + A → A is well defined by τ(u) = ln u. Now τσ(a) = ln [ea] = a and στ(u) = elnu = u hold, so σ and τ are inverses. Hence σ is a bijection. Finally σ(a + b) = ea+b = eaeb = σ(a)σ(b) for ab  A. Thus σ is a group isomorphism.
A. Thus σ is a group isomorphism.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
