3.4 Homomorphisms
1.
a. No. θ is a general ring homomorphism, because 42 = 4 in 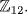 But θ(1) = 4, and 4 ≠ 1 in
But θ(1) = 4, and 4 ≠ 1 in 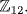
c. No. θ[(r, s) · (r′, s′)] = rr′ + ss′ need not equal
![]()
e. Yes. θ(fg) = (fg)(1) = f(1)g(1) = θ(f) · θ(g). Similarly for f ± g. The unity of 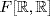 is
is 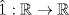 given by
given by 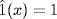 . Thus
. Thus 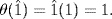
2.
a. Write θ(1) = e, and let s  S. Then s = θ(r) for some r
S. Then s = θ(r) for some r  R (θ is onto) so
R (θ is onto) so
![]()
Hence e is the unity of S.
3. If 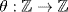 is a general ring homomorphism, let θ(1) = e. Then e2 = e so either e = 1 (θ a ring homomorphism) or e = 0. In the last case
is a general ring homomorphism, let θ(1) = e. Then e2 = e so either e = 1 (θ a ring homomorphism) or e = 0. In the last case
![]()
for all 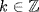 , so θ is trivial.
, so θ is trivial.
5. If z  Z(R) and s
Z(R) and s  R1, write s = θ(r), r
R1, write s = θ(r), r  R. Then
R. Then
![]()
Thus θ(z)  Z(R1). Any non-onto ring homomorphism θ : R → R1 where R1 is commutative shows this need not be equality.
Z(R1). Any non-onto ring homomorphism θ : R → R1 where R1 is commutative shows this need not be equality.
7. If  are ring homomorphisms then ϕθ is a group homomorphism and ϕθ(1R) = ϕ[θ(1R)] = ϕ(1S) = 1T,
are ring homomorphisms then ϕθ is a group homomorphism and ϕθ(1R) = ϕ[θ(1R)] = ϕ(1S) = 1T,
![]()
9. If R is a division ring and θ : R → S is a ring homomorphism, then ker θ is an ideal of R so ker θ = 0 or ker θ = R. If ker θ = 0 then θ is one-to-one so θ(R) ≅ R. If ker θ = R then θ(R) = 0. Thus the images of R are R and 0 up to isomorphism.
10. Clearly θ(r0) = θ(1) = 1 = [θ(r)]0. If θ(rn) = [θ(r)]n then
![]()
Hence (4) follows by induction.
11. In  this is x3 + x − 1 = 0. If x = 0, 1, 2, − 1 then x3 + x − 1 = − 1, 1, 1, 1, so there is no solution in
this is x3 + x − 1 = 0. If x = 0, 1, 2, − 1 then x3 + x − 1 = − 1, 1, 1, 1, so there is no solution in 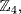 and hence none in
and hence none in 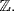
13. In 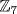 this is 4n2 = 2 and this has a solution (n = 2) in
this is 4n2 = 2 and this has a solution (n = 2) in 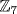 . However, in
. However, in 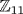 it is 7m2 = 9, or m2 = 8 · 9 = 72 = 6. But m2 = 0, 1, 3, 4, 5, 9 in
it is 7m2 = 9, or m2 = 8 · 9 = 72 = 6. But m2 = 0, 1, 3, 4, 5, 9 in 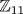 , so there is no solution in
, so there is no solution in 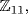 and hence no solution in
and hence no solution in 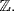
15. The inverse map is a group isomorphism by group theory. Given s and s1 in S then
![]()
Since σ is one-to-one, σ−1(s) · σ−1(s1) = σ−1(ss1).
17. R ≅ R because 1R : R → R is an automorphism. If R ≅ S, say σ : R → S in an isomorphism, then σ−1 : S → R is an isomorphism by Exercise 15, so S ≅ R. Finally if τ : S → T is an isomorphism, so is τσ : R → T so R ≅ T.
19.
a. θ(A) is an additive subgroup of S by Theorem 1 §2.10. If x  θ(A) and y
θ(A) and y  S = θ(R), let x = θ(a), y = θ(r), a
S = θ(R), let x = θ(a), y = θ(r), a  A, r
A, r  R. Then
R. Then
![]()
Similarly yx  θ(A), so θ(A) is an ideal of S.
θ(A), so θ(A) is an ideal of S.
21. Let 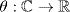 be a ring homomorphism. Then ker θ is an ideal of the field
be a ring homomorphism. Then ker θ is an ideal of the field  so
so 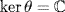 or ker θ = 0. But ker θ = 0 means
or ker θ = 0. But ker θ = 0 means 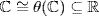 . Let θ(i) = a. Then a2 = [θ(i)]2 = θ(i2) = θ(− 1) = − 1, a contradiction as a is real. Since
. Let θ(i) = a. Then a2 = [θ(i)]2 = θ(i2) = θ(− 1) = − 1, a contradiction as a is real. Since 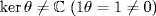 , there is no such θ.
, there is no such θ.
23.
a. If 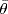 exists, then
exists, then 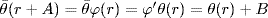 . Define
. Define 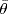 this way. Then
this way. Then 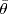 is well defined because
is well defined because
![]()
It is clearly a ring homomorphism and
![]()
for all r  R. Thus
R. Thus 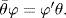
24.
a. Define θ : R∗ → aut R by θ(u) = σu for all u  R∗. Then
R∗. Then
![]()
for all r, so  ; that is, θ is a group homomorphism. Since θ(R∗) = inn R, this shows inn R is a subgroup of aut R. In fact inn R
; that is, θ is a group homomorphism. Since θ(R∗) = inn R, this shows inn R is a subgroup of aut R. In fact inn R 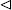 aut R. For if τ
aut R. For if τ  aut R and u
aut R and u  R∗, then
R∗, then 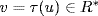 and
and 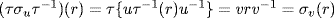 . Hence
. Hence 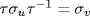 is in inn R, as required.
is in inn R, as required.
25.
a. e2 = baba = b1a = ba = e. Note that e(bra) = babra = b1ra = bra and, similarly, (bra)e = bra. This σ is a mapping R → eRe. Now σ(r + s) = σ(r) + σ(s) is onto and σ(r) · σ(s) = bra · bsa = br1sa = σ(rs). Finally σ(1) = ba = e shows σ is a ring homomorphism. If σ(r) = 0 then bra = 0 so r = 1r1 = (ab)r(ab) = a · 0 · b = 0. Thus σ is one-to-one. Finally, if r  eRe then r = ere = (ba)r(ba) = σ(arb). So σ is a ring isomorphism.
eRe then r = ere = (ba)r(ba) = σ(arb). So σ is a ring isomorphism.
27. We use the isomorphism theorem by finding an onto ring homomorphism θ : R → S × S that has A = ker θ. If 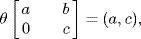 then θ is clearly onto, and the reader can verify that it is a ring homomorphism. Finally
then θ is clearly onto, and the reader can verify that it is a ring homomorphism. Finally 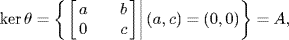 as required.
as required.
29.
a. Define 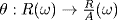 by
by 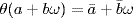 ,
, 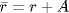 . This is an onto R-homomorphism and ker θ = A(ω). Done by the isomorphism theorem.
. This is an onto R-homomorphism and ker θ = A(ω). Done by the isomorphism theorem.
31. Note that e = (1, 0) is the unity of 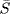 . Define θ : R = S × T → T by θ(s, t) = t. Then θ is an onto ring homomorphism and
. Define θ : R = S × T → T by θ(s, t) = t. Then θ is an onto ring homomorphism and 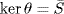 . Done by the isomorphism theorem.
. Done by the isomorphism theorem.
33. Define θ : R/A → R/B by θ(r + A) = r + B. This is well defined because r + A = s + A ⇒ r − s  A ⊆ B ⇒ r − s
A ⊆ B ⇒ r − s  B ⇒ r + B = s + B. It is clearly an onto ring homomorphism and ker θ = {r + A
B ⇒ r + B = s + B. It is clearly an onto ring homomorphism and ker θ = {r + A  r + B = 0} = B/A.
r + B = 0} = B/A.
35.
a. Define 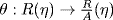 by
by 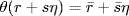 where
where 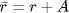 . This is an onto ring homomorphism and
. This is an onto ring homomorphism and 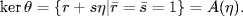
c. Observe first that r + sη is a unit in R(η) if and only if r ≠ 0 (then the inverse is r−1 − r1sr−1η). Let A ≠ 0 be an ideal of R(η) ; we show that A = Rη = {rη  r
r  R}. As A ≠ 0 let 0 ≠ a + bη
R}. As A ≠ 0 let 0 ≠ a + bη  A. Then a = 0 because A ≠ R(η), so b ≠ 0. But then η
A. Then a = 0 because A ≠ R(η), so b ≠ 0. But then η  A, whence Rη ⊆ A. If Rη ⊂ A let p + qη
A, whence Rη ⊆ A. If Rη ⊂ A let p + qη  A, p ≠ 0, whence A = R(η), as required.
A, p ≠ 0, whence A = R(η), as required.
36.
a. Define 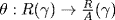 by
by 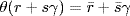 where
where  . This is an onto ring homomorphism and
. This is an onto ring homomorphism and 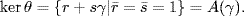
c. Let A ≠ 0, R(γ) be an ideal of R(γ). Since A ≠ 0 there exists 0 ≠ r + sγ  A, hence 1 + cg
A, hence 1 + cg  A for some c. Since (1 + cγ)(1 − cγ) = 1 − c2, the fact that A ≠ R(γ) means that c2 = 1. Hence c = ± 1 because R is a division ring. So either R(1 + γ) ⊆ A or R(1 − γ) ⊆ A.
A for some c. Since (1 + cγ)(1 − cγ) = 1 − c2, the fact that A ≠ R(γ) means that c2 = 1. Hence c = ± 1 because R is a division ring. So either R(1 + γ) ⊆ A or R(1 − γ) ⊆ A.
Now consider the maps θ : R(γ) → R and ϕ : R(γ) → R given by θ(r + sγ) = r + s and ϕ(r + sγ) = r − s for all r, s  R. These are onto ring homomorphisms, and ker θ = R(1 − γ) and ker ϕ = R(1 + γ). It follows from the isomorphism theorem that R(1 − γ) and R(1 + γ) are both maximal ideals. Hence A = R(1 − γ) or A = R(1 + γ).
R. These are onto ring homomorphisms, and ker θ = R(1 − γ) and ker ϕ = R(1 + γ). It follows from the isomorphism theorem that R(1 − γ) and R(1 + γ) are both maximal ideals. Hence A = R(1 − γ) or A = R(1 + γ).
37. Define 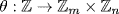 by
by 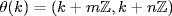 . This is a ring homomorphism and
. This is a ring homomorphism and 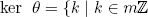 and
and 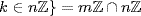 . Since m|t and n|t,
. Since m|t and n|t, 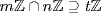 . Let
. Let 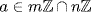 . Then m|a and n|a so t|a (because t = lcm(m, n)). Thus
. Then m|a and n|a so t|a (because t = lcm(m, n)). Thus 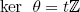 and so
and so 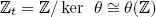 ; a subring of
; a subring of 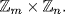
39. By Example 10 and induction, all ideals of R = R1 ×  × Rn look like A = A1 ×
× Rn look like A = A1 ×  × An, Ai an ideal of R. Hence
× An, Ai an ideal of R. Hence 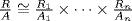 . Thus A is maximal if and only if exactly one of the Ak is maximal in Rk, and Ai = Ri if i ≠ k.
. Thus A is maximal if and only if exactly one of the Ak is maximal in Rk, and Ai = Ri if i ≠ k.
41. Put 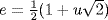 . Thus
. Thus 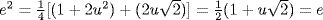 . Then
. Then  by Theorem 8 if we can show
by Theorem 8 if we can show  and
and 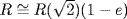 . Define
. Define 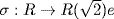 by σ(r) = re. This satisfies σ(r + s) = σ(r) + σ(s), and σ(rs) = σ(r)σ(s), and σ is one-to-one (σ(r) = 0 means
by σ(r) = re. This satisfies σ(r + s) = σ(r) + σ(s), and σ(rs) = σ(r)σ(s), and σ is one-to-one (σ(r) = 0 means 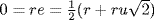 , so r = 0). If a, b
, so r = 0). If a, b  R then
R then
![]()
where r = a + 2bu. Thus σ is onto so 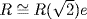 as rings. Similarly
as rings. Similarly  .
.
43.
a. Define θ : S → R by θ(f) = f(x). Then
![]()
![]()
![]()
The unity  of S is the constant function onto 1, so
of S is the constant function onto 1, so
![]()
Thus θ is a ring homomorphism, onto because, if r  R, r = θ(f) where f(t) = r for all t
R, r = θ(f) where f(t) = r for all t  X. Since ker θ = {f
X. Since ker θ = {f  S
S  f(x) = 0} we are done by the isomorphism theorem because R is simple.
f(x) = 0} we are done by the isomorphism theorem because R is simple.
44.
a. The map θ : R → R/A1 ×  × R/An with θ(r) = (r + A1, . . ., r + An) is a ring homomorphism with kernel A.
× R/An with θ(r) = (r + A1, . . ., r + An) is a ring homomorphism with kernel A.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
