11.1 Wedderburn's Theorem
1. If RM is simple, then M = Rx for any 0 ≠ x 
M. Hence α : R → M given by α(r) = rx is an onto R-linear map, so M ≅ R/L where L = ker(α), and L is maximal because M is simple. Conversely, R/L is simple for every maximal left ideal L. Conversely, R/L is simple for every maximal left ideal L again by Theorem 6 §8.1.
M. Hence α : R → M given by α(r) = rx is an onto R-linear map, so M ≅ R/L where L = ker(α), and L is maximal because M is simple. Conversely, R/L is simple for every maximal left ideal L. Conversely, R/L is simple for every maximal left ideal L again by Theorem 6 §8.1.
3. Define σ : Ra → Rb by σ(ra) = rb. This is well defined because ra = 0 implies rbR = r(aR) = 0, so rb = 0 . So σ is an onto homomorphism of left R-modules with σ(a) = b. Finally if σ(ra) = 0 then rb = 0 so (ra)R = r(aR) = r(bR) = 0, so ra = 0 . Hence σ is one-to-one.
5. If L1⊆ L2 ⊆ 
are left ideals of eRe, then RL1⊆ RL2 ⊆ are left ideals of R so RLn = RLn+1 = for some n by hypothesis. If i ≥ n, the fact that Li ⊆ eRe for each i, gives Li = eLi ⊆ eRLi = eRLn = eReLn ⊆ Ln. Hence Ln = Ln+1 = , as required.
are left ideals of eRe, then RL1⊆ RL2 ⊆ are left ideals of R so RLn = RLn+1 = for some n by hypothesis. If i ≥ n, the fact that Li ⊆ eRe for each i, gives Li = eLi ⊆ eRLi = eRLn = eReLn ⊆ Ln. Hence Ln = Ln+1 = , as required.
7. If RM is finitely generated, then 143 M is an image of Rn for some n ≥ 1 by Theorem 5 §7.1 and its Corollaries. Since Rn is noetherian as a left R-module (Corollary 1 of Lemma 2), the same is true of M by Lemma 2.
8. a. Observe that ann(X) is a left ideal for any X ⊆ M (note that ann (∅) = R) . Hence use the artinian condition to choose ann(X) minimal in
Then ann(M) ⊆ ann(X) is clear; we prove equality. If a ann(X), suppose that a ∉ ann(M), say am ≠ 0 with m M. Put Y = X ∪ {m} . Then ann(Y) ⊆ ann(X), so ann(Y) = ann(X) by minimality. But a ann(Y) and so am = 0, a contradiction. Hence a ann(M) and we have proved (a).
ann(X), suppose that a ∉ ann(M), say am ≠ 0 with m M. Put Y = X ∪ {m} . Then ann(Y) ⊆ ann(X), so ann(Y) = ann(X) by minimality. But a ann(Y) and so am = 0, a contradiction. Hence a ann(M) and we have proved (a).
9. Let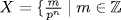 
and p does not divide m} . If 
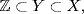where Y is a subgroup of X, choose 
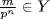with n maximal (n exists because Y ≠ X, 
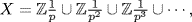and 
Then 
by Theorem 4 §1.2 because m and pn are relatively prime. Hence 
we claim that this is equality. To see this, let 
where p does not divide m′ . Then k ≤ n by the maximality of n, so 
whence 
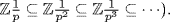and p does not divide m} . If where Y is a subgroup of X, choose with n maximal (n exists because Y ≠ X, and Then 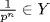by Theorem 4 §1.2 because m and pn are relatively prime. Hence 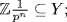we claim that this is equality. To see this, let 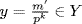where p does not divide m′ . Then k ≤ n by the maximality of n, so 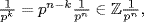whence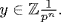
11. a. If x M then x− π(x) ker π, and it follows that M = π(M)+ ker π. If y π(M) ∩ ker π write y = π(z), z M. Since y ker π, we have 0 = π(y) = π2(z) = π(z) = y, so π(M)∩ ker π = 0 . This shows that M = π(M)⊕ ker π. (c). We have ker π = (1 − π)(M) because π(x) = 0 if and only if (1 − π)(x) = x. And π(M) = ker(1 − π) because (1 − π)(x) = 0 if and only if x = π(x).
M then x− π(x) ker π, and it follows that M = π(M)+ ker π. If y π(M) ∩ ker π write y = π(z), z M. Since y ker π, we have 0 = π(y) = π2(z) = π(z) = y, so π(M)∩ ker π = 0 . This shows that M = π(M)⊕ ker π. (c). We have ker π = (1 − π)(M) because π(x) = 0 if and only if (1 − π)(x) = x. And π(M) = ker(1 − π) because (1 − π)(x) = 0 if and only if x = π(x).
13. a. Suppose that K = K1⊕ K2 ⊕ is an infinite direct sum of nonzero submodules of M. Then K⊃ K2 ⊕ K3 ⊕ ⊃ K3 ⊕ K4 ⊃ contradicts the DCC, and K1⊂ K1 ⊕ K2 ⊂ K1 ⊕ K2 ⊕ K3 ⊂ contradicts the ACC.
is an infinite direct sum of nonzero submodules of M. Then K⊃ K2 ⊕ K3 ⊕ ⊃ K3 ⊕ K4 ⊃ contradicts the DCC, and K1⊂ K1 ⊕ K2 ⊂ K1 ⊕ K2 ⊕ K3 ⊂ contradicts the ACC.
15. Here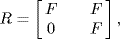 
and we consider 
Then e2 = e and 
is not simple as 
is a submodule. But end 
as rings.
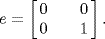and we consider Then e2 = e and 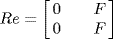is not simple as 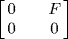is a submodule. But end 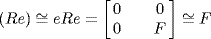as rings.
17. a. We have ker(α)⊆ ker(α2) ⊆ ker(α3) ⊆ so, since M is noetherian, there exists n ≥ 1 such that ker(αn) = ker(αn+1) = . If x ker(α) then (since αn is onto) write x = αn(y) for some y M. Then 0 = α(x) = αn+1(y), so y ker(αn+1) = ker(αn) . Hence x = αn(y) = 0, proving that ker(α) = 0.
so, since M is noetherian, there exists n ≥ 1 such that ker(αn) = ker(αn+1) = . If x ker(α) then (since αn is onto) write x = αn(y) for some y M. Then 0 = α(x) = αn+1(y), so y ker(αn+1) = ker(αn) . Hence x = αn(y) = 0, proving that ker(α) = 0.
19.
a. The easy verification that θ is an F-linear homomorphism of additive groups is left to the reader. To show that θ is one-to-one, suppose that θ(r) = 0 ; that is, uir = 0 for each i. If 1 = ∑ iaiui, then r = 1 · r = ∑ iaiuir = 0, so ker θ = 0 and θ is one-to-one. Finally, let θ(s) = [sij] so that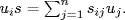 
Then:
Then:
Thus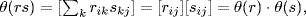 
and the proof is complete.
and the proof is complete.
c. 
c.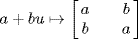 
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.