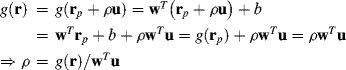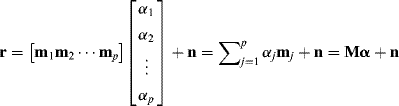2.3 Mixed Sample Analysis
In analogy with subsample analysis presented in Section 2.2, mixed sample analysis can be performed similarly with one key difference. In subsample analysis the background knowledge about the b considered in (2.13) is assumed to be unknown or can be obtained a posteriori directly from the data or a secondary data set, whereas in mixed sample analysis the target knowledge present in the r must be completely specified a priori. One fundamental task of mixed sample analysis is to perform spectral unmixing via linear spectral mixture analysis (LSMA). More specifically, LSMA assumes that a data sample vector r can be specified by a set of p known signals, ![]() as a linear mixture in terms of their respective mixing abundance fractions specified by
as a linear mixture in terms of their respective mixing abundance fractions specified by ![]() . When LSMA is used for classification, it classifies the r into one of these p signals,
. When LSMA is used for classification, it classifies the r into one of these p signals, ![]() . Using the five-fruit mixed juice described in the introduction as an example, the classification of mixed sample analysis is performed by assuming that the five fruits (apple, banana, lemon, orange, and strawberry) represent five known signals
. Using the five-fruit mixed juice described in the introduction as an example, the classification of mixed sample analysis is performed by assuming that the five fruits (apple, banana, lemon, orange, and strawberry) represent five known signals ![]() and the mixed juice r is an admixture of these five fruits with different concentrations
and the mixed juice r is an admixture of these five fruits with different concentrations ![]() . The classification of the mixed juice r is then performed in two ways. One is to determine which fruit is more likely to represent the mixed juice r, in which case the classification is performed by hard decisions. The other is to determine how much concentration of each fruit is contained in the mixed juice r, in which case the classification is performed by soft decisions via the concentration of each fruit estimated from the r as its abundance fraction. In analogy with pure sample-based signal detection making hard decisions and subsample-based signal detection making soft decisions that have been explored in Section 2.2 for detection, two similar types of classification, classification with hard decisions and classification with soft decisions, can be also derived in the same manner. The former can be considered as pure sample-based classification that labels a data sample vector r by a specific class, whereas the latter is mixed sample-based classification that estimates abundance fraction of each class present in a sample vector r as a likelihood of a particular class to be assigned to the r. More specifically, if there are p classes of interest to be assigned to a data sample vector r, the classification of r is performed by representing r as a p-dimensional vector,
. The classification of the mixed juice r is then performed in two ways. One is to determine which fruit is more likely to represent the mixed juice r, in which case the classification is performed by hard decisions. The other is to determine how much concentration of each fruit is contained in the mixed juice r, in which case the classification is performed by soft decisions via the concentration of each fruit estimated from the r as its abundance fraction. In analogy with pure sample-based signal detection making hard decisions and subsample-based signal detection making soft decisions that have been explored in Section 2.2 for detection, two similar types of classification, classification with hard decisions and classification with soft decisions, can be also derived in the same manner. The former can be considered as pure sample-based classification that labels a data sample vector r by a specific class, whereas the latter is mixed sample-based classification that estimates abundance fraction of each class present in a sample vector r as a likelihood of a particular class to be assigned to the r. More specifically, if there are p classes of interest to be assigned to a data sample vector r, the classification of r is performed by representing r as a p-dimensional vector, ![]() . When it is a pure-sample classification, only one
. When it is a pure-sample classification, only one ![]() for some j with
for some j with ![]() and the rest are zeros in which case only one class can be assigned to r. When it is a mixed-sample classification,
and the rest are zeros in which case only one class can be assigned to r. When it is a mixed-sample classification, ![]() is a real value, which indicates the likelihood of the jth signal sj to be assigned to the r via its abundance fraction estimate. Therefore, the pure sample-based classification is basically a class-label membership assignment that makes a hard decision on which class is more likely to represent the r. Two such well-known classification techniques will be reviewed: Fisher's linear discriminant analysis (FLDA) in Section 2.3.1.1 and support vector machine (SVM) in Section 2.3.1.2. On the other hand, the mixed sample classification essentially performs abundance fraction estimation that assigns a likelihood of a particular class to the sample r and the classification is performed by a set of likelihood values specified by abundance fractions. Two such mixed sample classification techniques, orthogonal subspace projection developed by Harsanyi and Chang (1994) and target-constrained interference-minimized filter (TCIMF) developed by Ren and Chang (2000), will be reviewed in Sections 2.3.2.1 and 2.3.2.2, both of which can be considered as extensions of CEM discussed in Section 2.2.3.
is a real value, which indicates the likelihood of the jth signal sj to be assigned to the r via its abundance fraction estimate. Therefore, the pure sample-based classification is basically a class-label membership assignment that makes a hard decision on which class is more likely to represent the r. Two such well-known classification techniques will be reviewed: Fisher's linear discriminant analysis (FLDA) in Section 2.3.1.1 and support vector machine (SVM) in Section 2.3.1.2. On the other hand, the mixed sample classification essentially performs abundance fraction estimation that assigns a likelihood of a particular class to the sample r and the classification is performed by a set of likelihood values specified by abundance fractions. Two such mixed sample classification techniques, orthogonal subspace projection developed by Harsanyi and Chang (1994) and target-constrained interference-minimized filter (TCIMF) developed by Ren and Chang (2000), will be reviewed in Sections 2.3.2.1 and 2.3.2.2, both of which can be considered as extensions of CEM discussed in Section 2.2.3.
2.3.1 Classification with Hard Decisions
In this section, we first describe two supervised pure sample-based classification techniques, FLDA and SVM, which require training data to perform hard-decision classification. From a view point of how to use training data, FLDA and SVM are completely different approaches. While FLDA can be considered as a statistics-based technique using training data on-average case, SVM can be regarded as a geometry-based technique using training data to find a hyperplane maximizing the distance between training samples on worst-case in the sense that training samples are near the separating hyperpalnes. In other words, an FLDA-generated classifier is derived by means and variances of training classes, whereas an SVM-generated classifier is derived by worst training data called support vectors. This is similar to what is used to evaluate computational complexity of an algorithm based on average case and worst case. As a result, in order for an FLDA-based classifier to perform effectively, the pool of training sample must be sufficiently large to produce reliable statistics of the data. By contrast, in order for an SVM-based classifier to perform well, it does not need a large set of training data. Instead, it requires the worst training data samples, that is, support vectors that are close to hyperplanes used to separate data samples. Therefore, both approaches have their own strengths and weaknesses depending upon provided training data.
2.3.1.1 Fisher's Linear Discriminant Analysis (FLDA)
In binary classification, we assume that there are nj training sample vectors given by ![]() for Cj,
for Cj, ![]() , with nj being the number of training sample vectors in the jth class Cj. Let μ be the global mean of the entire training sample vectors, denoted by
, with nj being the number of training sample vectors in the jth class Cj. Let μ be the global mean of the entire training sample vectors, denoted by ![]() , and μj be the mean of the training sample vectors in the jth class Cj, denoted by
, and μj be the mean of the training sample vectors in the jth class Cj, denoted by ![]() . The main idea of the FLDA is to find a vector that projects all data sample vectors into a new data space called feature space so that the projected data sample vectors in this feature space can have maximum separation of two classes, C1 and C2. Let w denote the projection vector with the projection carried out by
. The main idea of the FLDA is to find a vector that projects all data sample vectors into a new data space called feature space so that the projected data sample vectors in this feature space can have maximum separation of two classes, C1 and C2. Let w denote the projection vector with the projection carried out by ![]() . The training sample vectors
. The training sample vectors ![]() projected in this new feature space are then given by
projected in this new feature space are then given by ![]() with
with ![]() , and the mean and variance of the projected training vectors in Cj can be calculated as
, and the mean and variance of the projected training vectors in Cj can be calculated as ![]() and
and ![]() , respectively. The optimal projection vector w∗ that achieves the maximum separability of binary classification should be the one that separates the two projected means,
, respectively. The optimal projection vector w∗ that achieves the maximum separability of binary classification should be the one that separates the two projected means, ![]() and
and ![]() , as farther as possible while making two variances
, as farther as possible while making two variances ![]() and
and ![]() as small as possible. In order to accomplish these two goals simultaneously, the w∗ should be the one that maximizes the following criterion:
as small as possible. In order to accomplish these two goals simultaneously, the w∗ should be the one that maximizes the following criterion:
Or alternatively, (2.34) can be reexpressed in terms of matrix forms called Fisher's ratio or Rayleigh's quotient, which is
where SB and SW are referred as between-class and within-class scatter matrices, respectively, and given by
and
The solution for w to maximize (2.35) is given in Bischop (1995) by
which specifies a projection vector w∗ subject to a scale constant. Interestingly, letting two classes be specified by the target class and the background class with their respective means, denoted by target mean ![]() and background mean
and background mean ![]() , (2.38) becomes
, (2.38) becomes
Comparing (2.39) to (2.17) both have the same form except that K−1 in (2.17) is replaced with ![]() in (2.32). More details about this relationship can be found in Chang and Ji (2006) and Chapters 13, 14 of this book.
in (2.32). More details about this relationship can be found in Chang and Ji (2006) and Chapters 13, 14 of this book.
A remark on FLDA for binary classification is noteworthy. It has been shown in Bischop (1995) that FLDA-based binary classification is identical to least squares-based approach. In addition, FLDA-based binary classification is also shown by Chang et al. (2006) to be identical to Otsu's image thresholding method. However, it is interesting to note that none of these two can be applied to FLDA-based multiclassification.
In order to extend FLDA for two-class classification to multiple-class classification, assume that there are p classes of interest, ![]() and nt training sample vectors given by
and nt training sample vectors given by ![]() for p-class classification, with nj being the number of training sample vectors in the jth class Cj. Let μ be the global mean of the entire training sample vectors, denoted by
for p-class classification, with nj being the number of training sample vectors in the jth class Cj. Let μ be the global mean of the entire training sample vectors, denoted by ![]() , and μj be the mean of the training sample vectors in the jth class Cj, denoted by
, and μj be the mean of the training sample vectors in the jth class Cj, denoted by ![]() . Now, we can extend (2.36) and (2.37) to define the within-class scatter matrix, SW and between-class scatter matrix SB for p classes as follows.
. Now, we can extend (2.36) and (2.37) to define the within-class scatter matrix, SW and between-class scatter matrix SB for p classes as follows.
Using (2.40) and (2.41), Fisher's ratio in (2.35) is then generalized and given in Bischop (1995) by
p-Class FLDA classification is to find a set of feature vectors specified by the matrix WFLDA that maximize Fisher's ratio specified by (2.42) where the number of feature vectors found by WFLDA is p − 1, which is determined by the number of classes, p. These FLDA-obtained p − 1 feature vectors specify boundaries among p classes. More details can be found in Duda and Hart (1973), Bischop (1995, 2006), and Section 9.2.3 in Chang (2003a).
Since the feature matrix WFLDA obtained from (2.42) is a matrix that specifies p − 1 feature vectors, directly finding WFLDA by maximizing (2.42) may encounter singularity problems. Instead of solving p − 1 feature vectors in WFLDA all together from (2.42), an alternative solution is to find these p − 1 feature vectors one at a time by solving (2.38). In other words, solving a multiple-class FLDA problem can be accomplished by solving a sequence of two-class FLDA problems one after another successively. A specific algorithm in doing so is described as follows.
Algorithm for finding successive feature vectors for FLDA
It is worth noting that the key for the above algorithm to work is to assume that all the p − 1 feature factors are orthogonal to each other. This is true because solving the feature vector via (2.38) is equivalent to finding an eigenvector associated with the largest eigenvalue of ![]() . As a result, two different feature vectors result in two distinct eigenvectors that are always orthogonal. The OSP is used to guarantee that its feature spaces from which feature vectors are generated are indeed orthogonal to each other.
. As a result, two different feature vectors result in two distinct eigenvectors that are always orthogonal. The OSP is used to guarantee that its feature spaces from which feature vectors are generated are indeed orthogonal to each other.
2.3.1.2 Support Vector Machines (SVM)
In this section, we describe another interesting pure-sample classifier, support vector machine, which uses a different classification criterion. Instead of maximizing the distance between two class means and minimizing sum of the distances within each of two classes as measured by Fisher's ratio in (2.35), SVM uses a set of training sample vectors, referred to as support vectors for each of two classes and maximizes the distance between the support vectors in these two classes. Following the same approach presented in Chapter 6 of Haykin (1999), its idea can be described mathematically as follows.
Assume that a linear discriminant function, y = g(r) is specified by
(2.43) ![]()
where w is a weighting vector that determines the performance of y = g(r) based on the sample vector r and b is a bias.
Consider a two-class classification problem with a given set of training data ![]() where
where ![]() are n training samples with their associated binary decisions
are n training samples with their associated binary decisions ![]() specified by either 1 or 0. For each pair of
specified by either 1 or 0. For each pair of ![]() it satisfies
it satisfies
where
specifies a hyperplane that is a decision boundary that separates two classes. If n be the normal vector of the hyperplane specified by (2.45), then (2.45) can be reexpressed as
which indicates that the n is orthogonal to the hyperplane. If we further let u be the normalized unit vector of n, that is, ![]() , then any data sample vector r in the data can be represented by
, then any data sample vector r in the data can be represented by
(2.47) ![]()
where rp is the projected point of r onto the hyperplane with ![]() and the scalar ρ is the distance of the data sample vector x from its projected vector xp which can be calculated as follows.
and the scalar ρ is the distance of the data sample vector x from its projected vector xp which can be calculated as follows.
If w = n, then ![]() , which implies that
, which implies that ![]() . In particular, if r = 0 and w = n,
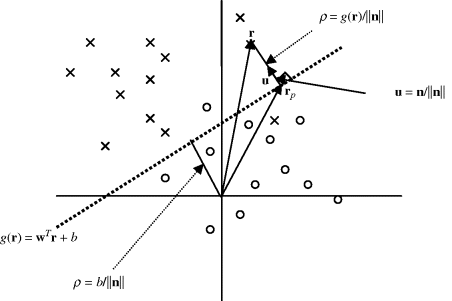
. In particular, if r = 0 and w = n, ![]() . Figure 2.3 depicts their graphical relationship.
. Figure 2.3 depicts their graphical relationship.
Figure 2.3 Illustration of linear discriminant function g(r) = wTr + b.
An SVM is a linear discriminant function that can be used as a linear binary classifier. It was originally developed in statistical machine learning theory by Vapnik (1998). For a given set of training data, ![]() , an SVM finds a weighting vector w and bias b that satisfy
, an SVM finds a weighting vector w and bias b that satisfy
and maximize the margin of separation defined by distance between a hyperplane and closest data samples. In particular, (2.44) can be rederived by incorporating its binary decision into the discriminant function (2.49) as follows
It should be noted that (2.49) is modified from (2.44) by replacing decision 0 with decision 1 when ![]() so that two decisions in (2.49) can be combined in to one equation (2.50).
so that two decisions in (2.49) can be combined in to one equation (2.50).
According to (2.48) the distance ρ between a sample vector r and its projected vector on the hyperplane g(r) = wTr + b = 0 is specified by ![]() , with w being the normal vector of the hyperplane. Since g(x) takes only +1 or −1, the distance ρ is then defined by
, with w being the normal vector of the hyperplane. Since g(x) takes only +1 or −1, the distance ρ is then defined by
Using (2.51) we define the margin of separation between two classes as
By virtue of (2.50)–(2.52), the linear separability problem for the SVM is to find an optimal weight vector w∗ that maximizes the distance specified by (2.52), which is equivalent to minimizing
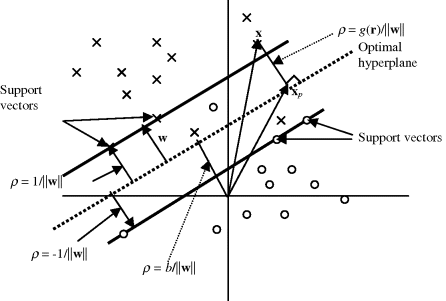
subject to constraints specified by (2.50). Figure 2.4 illustrates the concept of the SVM where two classes of data sample vectors are denoted by “open circles” and “crosses” and the vectors satisfying the equality of (2.50) are called support vectors.
Figure 2.4 Illustration of SVM.
In order to solve the constrained optimization problem specified by (2.53), we introduce a Lagrangian defined by
which takes care of the cost function given by (2.54) along with constraints specified by (2.46). Differentiating J(w, b, a) in (2.54) with respect to w and b yields
along with the constraint (2.50)
(2.57) ![]()
Expanding J(w, b, a) and wTw we obtain
(2.59) ![]()
Using (2.55) and (2.56) we can reformulate J(w, b, a) as
In light of (2.60) an alternative form of the linear separability problem for the SVM can be formulated as follows.
Alternative Form of Linear Separability Problem for SVM
Given a set of training pool, ![]() , find a set of Lagrange multiplier vector
, find a set of Lagrange multiplier vector ![]() that maximizes Q(a) is given by (2.60) subject to the following constraints
that maximizes Q(a) is given by (2.60) subject to the following constraints
Solution to the above optimization problem is given by
(2.61) ![]()
(2.62) ![]()
with rs is a support vector on the hyperplane with its decision ds = +1.
By far the SVM discussed above was developed to separate two classes that are linearly separable. That is, the data sample vectors in two classes can be separated by a distance greater than ρ from the hyperplane shown in Figure 2.4. However, in many applications, such desired situations may not occur. In other words, some data sample vectors fall in the region within the distance less than ρ from the hyperplane or even on the wrong side of the hyperplane. These data sample vectors can be considered to be either bad or confusing data sample vectors and they cannot be linearly separated. In this case, the SVM developed for linear separable problems outlined by (2.58)–(2.60) must be rederived to take care of such confusing data sample vectors. In order for linear SVMs to solve linear nonseparable problems, two approaches are of particular interest. One is a kernel-based approach that will be discussed in detail in Section 30.3. The other is to introduce a set of slack variables into SVMs to resolve the dilemma caused by confusing data sample vectors. Specifically, a new set of positive parameters, denoted by ![]() and referred to as slack variables, must be introduced to measure the deviation of a data sample vector from the ideal condition of linear separability, in which case
and referred to as slack variables, must be introduced to measure the deviation of a data sample vector from the ideal condition of linear separability, in which case ![]() . However, if
. However, if ![]() , the ith data sample vector xi falls within the region with distance less than the margin of separation but on correct side of the decision surface specified by the hyperplane. On the other hand, if
, the ith data sample vector xi falls within the region with distance less than the margin of separation but on correct side of the decision surface specified by the hyperplane. On the other hand, if ![]() , the ith data sample vector xi falls on the wrong side of its decision surface. In light of the mathematical interpretation, these issues can be addressed by the following inequalities:
, the ith data sample vector xi falls on the wrong side of its decision surface. In light of the mathematical interpretation, these issues can be addressed by the following inequalities:
By incorporating (2.63) and (2.64) in (2.53) the object function Φ(w) can be modified as
By virtue of (2.63)–(2.65) a linear nonseparable problem solved by the SVM can be described as follows.
Given a set of training pools, ![]() , find an optimal weight vector wSVM and bias bSVM such that they satisfy the constraints specified by (2.63) and (2.64) and such that the pair of (wSVM, bSVM) and
, find an optimal weight vector wSVM and bias bSVM such that they satisfy the constraints specified by (2.63) and (2.64) and such that the pair of (wSVM, bSVM) and ![]() minimizes (2.65). Or an alternative form can be obtained as follows.
minimizes (2.65). Or an alternative form can be obtained as follows.
Given a set of training pool, ![]() , find a set of Lagrange multiplier vectors
, find a set of Lagrange multiplier vectors ![]() that maximize Q(a) given by (2.60) subject to the following constraints:
that maximize Q(a) given by (2.60) subject to the following constraints:
The optimal solution wSVM to the above optimization problem is given by
(2.66) ![]()
where ns is the number of support vectors.
It should be noted that the slack variables ![]() along with their Lagrange multipliers
along with their Lagrange multipliers ![]() that are used to constrain non-negativity of
that are used to constrain non-negativity of ![]() do not appear in the alternative form. Instead, the constraint constant C associated with the slack variables is included to bound the Lagrange multiplier
do not appear in the alternative form. Instead, the constraint constant C associated with the slack variables is included to bound the Lagrange multiplier ![]() from above. Nevertheless, by means of (2.60) we can still derive the following equations that include the slack variables
from above. Nevertheless, by means of (2.60) we can still derive the following equations that include the slack variables ![]() and their associated Lagrange multipliers
and their associated Lagrange multipliers ![]() .
.
Differentiating with the slack variables, ![]() and setting to zero yields
and setting to zero yields
Combining (2.68) and (2.69) results in
In this case, the bSVM can be obtained by taking any data sample vector xi with ![]() (in which case,
(in which case, ![]() due to (2.70)) and (2.67).
due to (2.70)) and (2.67).
As originally designed, SVM is a binary classifier. In order to extend SVM to a multiclass classifier, two approaches have been proposed in the past. One is the so-called one-against-all also known as winner-take-all approach, which reduces a multiclass classification problem to a set of two-class binary classification problems, each of which is produced by SVM to separate one particular training data sample vector from the rest of training sample vectors. That is, let Ω denote the set of classes ![]() and nC be the number of classes. For each training sample vector r, we consider two classes,
and nC be the number of classes. For each training sample vector r, we consider two classes, ![]() and
and ![]() . The discriminant function or decision function of a sample vector x derived by the SVM that separates the class ωk from
. The discriminant function or decision function of a sample vector x derived by the SVM that separates the class ωk from ![]() is given by
is given by
The data sample vector r is then classified into the class denoted by class(r) that yields the maximum value of yk(r) over all ![]() , which is
, which is
(2.72) ![]()
A second approach is to reduce a multiclass classification problem to a set of binary classification problems by pairing any two classes as a binary classification problem. As a result, there are ![]() pairwise binary classification problems. In other words, each binary classification is specified by two separate classes ωk and ωl. The SVM separating these two classes is specified by its discriminant function or decision function ykl(ri) for a sample vector r. If we define a score function of a sample vector r associated with class ωk by
pairwise binary classification problems. In other words, each binary classification is specified by two separate classes ωk and ωl. The SVM separating these two classes is specified by its discriminant function or decision function ykl(ri) for a sample vector r. If we define a score function of a sample vector r associated with class ωk by
(2.73) ![]()
The class assigned to r is one that yields the maximum score given by
(2.74) ![]()
The issues arising from using SVM to perform multi-classification are similar to those encountered in FLDA discussed in Section 2.3.1.1 and are addressed in detail in Bischop (2006).
2.3.2 Classification with Soft Decisions
Recall that the model in (2.13) is used for subsample target detection where the desired target t is assumed to partially occupy the sample vector r as a subsample target with its abundance fraction specified by α and the background b is accounted for the remaining abundance (1 − α). In this case, the algorithms developed for subsample target detection are designed to enhance the detectability of the target of interest while suppressing the background as much as possible. The CEM developed in Section 2.2.3 was the one that adopts this design rationale and philosophy. However, this is not true for mixed sample analysis where the background knowledge is completely specified by other known target signals which are also of interest. In order for CEM to be able to perform mixed sample analysis, several CEM-based mixed sample classification techniques were investigated in Chang (2002b) and presented in Chang (2003a), among which two techniques are of particular interest, orthogonal subspace projection derived from linear mixture analysis and target-constrained interference-minimized filter, which will be discussed in this and following sections.
2.3.2.1 Orthogonal Subspace Projection (OSP)
The OSP was originally developed by Harsanyi and Chang (1994) for linear spectral mixture analysis. Its idea is similar to that used in the ASD discussed in Section 2.2.2.2. It makes an assumption that a data sample vector r is completely characterized by a linear mixture of a finite number of so-called endmembers that are assumed to be present in the image data. More specifically, suppose that L is the number of spectral bands and r is an L-dimensional data sample vector. Let ![]() be p endmembers, which are generally referred to as digital numbers (DNs). The data sample r can be then linearly represented by
be p endmembers, which are generally referred to as digital numbers (DNs). The data sample r can be then linearly represented by ![]() with appropriate abundance fractions specified by
with appropriate abundance fractions specified by ![]() . In other words, let r be an
. In other words, let r be an ![]() column vector, M be an endmember signature matrix, denoted by
column vector, M be an endmember signature matrix, denoted by ![]() , and
, and ![]() be a
be a ![]() abundance column vector associated with r where αj denotes the abundance fraction of the jth endmember mj present in the r. Then an L-dimensional data sample r can be represented by a linear mixture model as follows.
abundance column vector associated with r where αj denotes the abundance fraction of the jth endmember mj present in the r. Then an L-dimensional data sample r can be represented by a linear mixture model as follows.
where n is noise or can be interpreted as either a measurement or a model error.
If we assume that the target signal of interest is mp without loss of generality and compare (2.75) with (2.13), an immediate finding is that the subsample target of interest t and the background b in (2.13) are now represented by mp, with the b completely characterized by the remaining p − 1 target signals, ![]() as a background matrix
as a background matrix ![]() . With this interpretation the model (2.75) can be reexpressed as a subsample target detection model similar to (2.13) and given by
. With this interpretation the model (2.75) can be reexpressed as a subsample target detection model similar to (2.13) and given by
where mp = t with αp = α and b = B, with (1 − α) replaced by the p − 1 dimensional abundance vector ![]() .
.
It has been shown in Harsanyi and Chang (1994), Chang (2003a), and Chang (2005) that the optimal solution of αp to (2.76), ![]() is given by an OSP projector δOSP(r)
is given by an OSP projector δOSP(r)
where the desired signal d is designated by the signal of interest mp, ![]() is undesired signal matrix, and
is undesired signal matrix, and ![]() is an undesired signal subspace projector given by
is an undesired signal subspace projector given by
with ![]() being the pseudoinverse of U. The notation
being the pseudoinverse of U. The notation ![]() in
in ![]() indicates that the projector
indicates that the projector ![]() maps the data sample r into the orthogonal complement of
maps the data sample r into the orthogonal complement of ![]() , denoted by
, denoted by ![]() . If we compare (2.77) to (2.27), we immediately find that both ASD and OSP are derived from maximizing SCR or SNR and also yield the same detector structure except that the subtarget signal t and the inverse of the sample covariance matrix, K−1 in (2.27) and (2.28) are replaced by the desired signal d to be classified and the undesired signal subspace projector
. If we compare (2.77) to (2.27), we immediately find that both ASD and OSP are derived from maximizing SCR or SNR and also yield the same detector structure except that the subtarget signal t and the inverse of the sample covariance matrix, K−1 in (2.27) and (2.28) are replaced by the desired signal d to be classified and the undesired signal subspace projector ![]() in (2.85), respectively. This is because OSP has prior knowledge about the undesired signals,
in (2.85), respectively. This is because OSP has prior knowledge about the undesired signals, ![]() and takes advantage of
and takes advantage of ![]() to annihilate such unwanted interference prior to the use of matched filter. By contrast, ASD does not have such prior knowledge about
to annihilate such unwanted interference prior to the use of matched filter. By contrast, ASD does not have such prior knowledge about ![]() . As a consequence, it makes use of a whiten matrix K−1 resulting from the sample covariance matrix K to suppress unknown interference. Detailed discussion on this issue can be found in Chapter 12 and Chang (2005).
. As a consequence, it makes use of a whiten matrix K−1 resulting from the sample covariance matrix K to suppress unknown interference. Detailed discussion on this issue can be found in Chapter 12 and Chang (2005).
By virtue of (2.77) δOSP(r) performs classification with soft decisions by estimating the abundance fractions of each of p endmembers ![]() in such a way that each of p endmembers
in such a way that each of p endmembers ![]() is designated as a subsample target of interest specified by the desired signal d, while other signals are considered as undesired signals to form an undesired signal matrix U.
is designated as a subsample target of interest specified by the desired signal d, while other signals are considered as undesired signals to form an undesired signal matrix U.
It was shown in Chang (1998) that δOSP(r) in (2.77) performed as a detector rather than an estimator since it did not consider the estimation accuracy of abundance αp. In order to make δOSP(r) perform an estimator, a scaling constant ![]() is included in δOSP(r) to correct the estimation error resulting from δOSP(r). The resultant estimator turns out to be a least squares-based estimator given by
is included in δOSP(r) to correct the estimation error resulting from δOSP(r). The resultant estimator turns out to be a least squares-based estimator given by
which has a form similar to that of CEM in (2.33) except that the subtarget signal t and the inverse of the sample covariance matrix, R−1 in (2.33) are replaced by the desired signal d to be classified and the undesired signal subspace projector, ![]() in (2.77). Furthermore, comparing (2.79) to (2.28), both ASD in (2.28) and LSOSP in (2.77) judiciously select an appropriate constant κ,
in (2.77). Furthermore, comparing (2.79) to (2.28), both ASD in (2.28) and LSOSP in (2.77) judiciously select an appropriate constant κ, ![]() in (2.27) and
in (2.27) and ![]() in (2.77) to account for the error caused by estimating the abundance of target signal t in (2.13) or desired signal d in (2.75).
in (2.77) to account for the error caused by estimating the abundance of target signal t in (2.13) or desired signal d in (2.75).
2.3.2.2 Target-Constrained Interference-Minimized Filter (TCIMF)
As shown in Section 2.2.2 CEM was designed to detect a single subsample target. If there are multiple subsample targets in the sample vector r, one subsample target must be carried out by CEM at a time. On the other hand, the OSP derived in (2.77) and (2.79) is developed for mixed sample classification for each of endmembers, ![]() . However, in reality, background may not be completely characterized by known signals. In most cases, interferers that cannot be identified a priori may be also present in the sample vector r. The OSP is not designed to account for such unknown interferers. In order to extend the capability of CEM to perform detection of multiple targets as well as take advantage of the capability of OSP in suppressing unknown interference a TCIMF was recently developed by Ren and Chang (2000), which can be viewed as a generalization of the OSP and CEM.
. However, in reality, background may not be completely characterized by known signals. In most cases, interferers that cannot be identified a priori may be also present in the sample vector r. The OSP is not designed to account for such unknown interferers. In order to extend the capability of CEM to perform detection of multiple targets as well as take advantage of the capability of OSP in suppressing unknown interference a TCIMF was recently developed by Ren and Chang (2000), which can be viewed as a generalization of the OSP and CEM.
Let ![]() denote the desired target signature matrix and
denote the desired target signature matrix and ![]() be the undesired target signature matrix where nD and nU are the number of the desired target signals and the number of the undesired target signals, respectively. Now, we can develop an FIR filter that passes the desired target signals in D using an
be the undesired target signature matrix where nD and nU are the number of the desired target signals and the number of the undesired target signals, respectively. Now, we can develop an FIR filter that passes the desired target signals in D using an ![]() unity constraint vector
unity constraint vector ![]() while annihilating the undesired target signals in U using an
while annihilating the undesired target signals in U using an ![]() zero constraint vector
zero constraint vector ![]() . In doing so, the constraint in (2.31) is replaced by
. In doing so, the constraint in (2.31) is replaced by
(2.80) ![]()
and the optimization problem specified by (2.31) becomes the following linearly constrained optimization problem
The filter solving (2.81) is called target-constrained interference-minimized filter (TCIMF) (Ren and Chang, 2000) and given by
(2.82) ![]()
with the optimal weight vector, wTCIMF given by
(2.83) ![]()
A discussion on the relationship between OSP and CEM via TCIMF can be found in Chang (2002, 2003a, 2005). For example, if ![]() with
with ![]() and
and ![]() with
with ![]() , δTCIMF(r) performs like δOSP(r). On the other hand, if
, δTCIMF(r) performs like δOSP(r). On the other hand, if ![]() with
with ![]() and
and ![]() with
with ![]() , δTCIMF(r) performs like δCEM(r). More details on OSP in comparison with CEM and TCIMF can be found in Chapter 12.
, δTCIMF(r) performs like δCEM(r). More details on OSP in comparison with CEM and TCIMF can be found in Chapter 12.