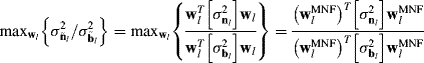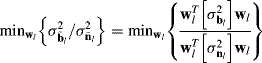6.2 Dimensionality Reduction by Second-Order Statistics-Based Component Analysis Transforms

A CA transform generally transforms the image data into a set of data components so that the correlation among the transformed data components is uncorrelated according to a criterion. More specifically, a component transform represents a data space by a set of its generated data components. Two second-order component transforms have been widely used in remote sensing image processing, which are variance-based PCA transforms and SNR-based transforms and discussed as follows.

6.2.1 Eigen Component Analysis Transforms

The simplest eigen-CA transforms are those based on data variance. PCA represents this type of data variance-based CA transforms.

6.2.1.1 Principal Components Analysis

The principal components analysis (PCA), also known as Hotelling transform (Gonalez and Woods, 2002) as well as principal components transformation (PCT) (Richards and Jia, 1999; Schowengerdt, 1997), is an optimal transform to represent data in the sense of data variance. It can be considered as a discrete time version of the Karhunen–Loeve transform (KLT) in signal processing and communications (Poor, 1994) that is an optimal transform using eigenfunctions as basis functions to represent and de-correlate a function in the sense of mean-squared error. It is generally referred to as Karhunen–Loeve expansion that represents a function as a series in terms of eigenfunctions where these eigenfunctions are continuous-time functions. When they are sampled at discrete time instants, eigenfunctions become eigenvectors in a discrete case, in which case KLT is reduced to PCA. So, technically speaking, KLT used in hyperspectral data compression is indeed the principal components analysis (PCA) not what it was originally developed in statistical signal processing and communications in at least two major key aspects. The first and foremost is the used criterion. While KLT is a mean-squared error (MSE)-based transform that assumes the availability of data probability distribution to perform “mean” in terms of statistical expectation, PCA makes use of the sample covariance matrix without assuming the data probability distribution in which case PCA should be considered as a “least squares error (LSE)”-based transform, not an MSE-based transform where LSE is actually the sample variance. Secondly, KLT is generally referred to as KL expansion in statistical signal processing where a signal can be decomposed as a series of orthogonal functions, to be called eigenfunctions. For example, Fourier transform is a special case of KLT where the used sinusoidal functions are basically eigenfunctions. Therefore, in general, KLT is a continuous time transform function. By contrast, PCA is a matrix transform used to de-correlate data sample vectors into linear combinations of using eigenvectors as basis vectors for their data representations with eigenvalues as their corresponding coefficients. In light of this interpretation PCA is indeed a discrete time of KL expansion. Unfortunately, KLT has been widely abused in image processing where the image data are represented by matrices in which case KLT should be implemented as its discrete-time version, PCA. It seems that such key differences have been overlooked in hyperspectral data compression. The idea of PCA can be briefly described as follows.

Assume that is a set of L-dimensional image pixel vectors and μ is the mean of the sample pool S obtained by . Let X be the sample data matrix formed by . Then the sample covariance matrix of the S is obtained by . If we further assume that is the set of eigenvalues obtained from the covariance matrix K and are their corresponding unit eigenvectors, that is, , we can define a diagonal matrix D_σ with variances along the diagonal line as

(6.1)

and an eigenvector matrix Λ specified by as

(6.2)

such that

(6.3)

Using the eigenvector matrix Λ a linear transform ξ_Λ defined by

(6.4)

transforms every data sample r_i to a new data sample, by

(6.5)

As a result, the mean of new ξ_Λ-transferred data samples becomes and its resulting covariance matrix is reduced to a diagonal matrix given by

(6.6)

Equation (6.6) implies that the ξ_Λ-transferred data matrix has been de-correlated or whitened by the matrix Λ that is referred to as a whitening matrix (Poor, 1994). The transform ξ_Λ defined by (6.5) is generally called principal component transform and the lth component of is formed by

(6.7)

and is called the lth principal component (PC) that consists of that are -transferred data samples corresponding the lth eigenvalue λ_l. PCA is a process that implements the transform ξ_Λ defined by (6.4) to obtain a set of principal components (PCs) via (6.5) or (6.7) with all . In order to achieve DR, only the PCs specified by eigenvectors that correspond to first q largest eigenvalues will be retained, while the PCs specified by eigenvectors corresponding to the remaining (L–q) smaller eigenvalues will be discarded. The same process can be accomplished by the singular value decomposition (SVD) to be described in Section 6.2.1.6.

6.2.1.2 Standardized Principal Components Analysis

In PCA, its focus is placed on the variances of the image pixel vectors . It has been shown by Singh and Harison (1985) that in some applications in remote sensing, it may be more effective to deal with data co-variances rather than data variances. Such co-variance-based PCA is called standardized principal components analysis (SPCA).

Assume that the covariance matrix K is given by

(6.8)

with the lth variance and (i,j)-covariance denoted by and σ_ij, respectively. Now we define a standard deviation matrix of K via (6.78) as that is the diagonal matrix of the form

(6.9)

Then is called a standardized sample of r_i and K can be expressed as

(6.10)

where R_K is called the correlation coefficient matrix defined by

(6.11)

with and . It should be noted that the R_K in (6.11) is not the sample correlation matrix R. The κ_ij in R_K is generally called the (i,j)th correlation coefficient of K.

Using (6.2) is the eigenvector matrix of K formed by its unit eigenvectors . Through (6.10) we can obtain

(6.12)

that is the identity matrix. Combining the eigenvector matrix Λ in (6.2) and the diagonal matrix obtained by (6.9) we can define a linear transform by

(6.13)

that is called standardized PCA (SPCA) and denoted by

(6.14)

Using (6.12) and (6.14), the covariance matrix of the new data samples that are obtained from by the SPCA in (6.14) becomes an identity matrix.

Similarly, in analogy with the decomposition of K, its inverse matrix K⁻¹ can be also decomposed as

(6.15)

where

(6.16)

and are variances of K⁻¹ and

(6.17)

with η_ij being the (i,j)th correlation coefficient of K⁻¹ and . It turns out that the in (6.16) can be related to the in (6.9) by the following formula:

(6.18)

where is a multiple correlation coefficient of the data in the lth dimension on all other dimensions obtained by using the multiple regression theory. So, is the reciprocal of a good noise variance estimate for the lth-dimensional data space. It should be noted that the D_ζ in (6.16) is not an inverse of the D_σ in (6.9), nor is in (6.17). The major advantage of using ζ_l over is that as shown in (6.18), ζ_l removes its correlation on other ζ_l's for , while does not. Like PCA, SPCA achieves DR by only retaining standard PCs corresponding to eigenvectors that are associated with first q largest eigenvalues.

6.2.1.3 Singular Value Decomposition

Another eigen-CA transform is the singular value decomposition (SVD). Unlike PCA that is primarily designed to de-correlate the covariance matrix, SVD is one of most widely used techniques in systems, communications, and signal processing to resolve issues caused by ill-conditioned systems, such as underdetermined or overdetermined least squares system. It provides a matrix factorization of an arbitrary matrix into a product of two unitary matrices and a diagonal matrix. More specifically, let be an real matrix. Define two matrices and that can, respectively, be referred to as outer product matrix and inner product matrix where both matrices and are symmetric, semidefinite with non-negative real eigenvalues, and have the same rank. In particular, when is an m-dimensional column vector x, the outer product matrix is an matrix, , and the inner product matrix is a scalar, both of which have rank 1. In this case, the only nonzero eigenvalue of the outer product matrix of is specified by its inner product matrix .

Assume that the eigenvalues of and are and that can be arranged in descending order in magnitude as follows:

(6.19)

where . Since both matrices and have the same rank and also identical nonzero eigenvalues, and for all . Then the set of square root of eigenvalues in (6.19)

(6.20)

is called the singular values of the matrix (Chen, 1999). Now we can further decompose the matrix into the following factorization form:

(6.21)

where is an unitary matrix with its column vectors being orthonormalized eigenvectors of the matrix so that , is an unitary matrix with its column vectors being orthonormalized eigenvectors of the matrix so that , and is an diagonal matrix with its diagonal entries specified by the singular values of and arranged in descending order in magnitude, . Specifically, if the rank of is r, then is a square matrix of size with .

In hyperspectral data exploitation, assume that is a set of entire image pixel vectors or a set of training samples in a hyperspectral image. in (6.21) can be considered by either a data matrix formed by data samples/image pixel vectors with the subscript m and n denoting the total number of spectral bands and the number of image pixel vectors (such as total number of image pixel vectors or training samples), respectively, or a sample correlation/covariance matrix / formed by the total number of data samples/image pixel vectors with being the total number of spectral bands, and q being the number of dimensions to be retained, respectively. In the former case, the matrix in (6.21) is formed by data sample vectors, with the ith column vector specified by the ith image pixel vector r_i. So, the resulting matrix is represented by with . In (6.21) and are called left and right singular vector matrices of and they are generally different. The singular values of are simply square root of non-negative eigenvalues of , . In other words, if we interpret eigenvalues as variances, the singular values are simply their standard deviations. As for the latter case, the matrix in (6.21) is formed by the data sample correlation matrix, , that becomes the outer product matrix of , scaled by a constant . The singular values of are exactly the same non-negative eigenvalues of , and the left and right singular vector matrices of , , and turn out to be the same as the eigenvector matrix Λ described by (6.2); (6.21) is reduced to (6.3), in which case SVD becomes PCA described in Section 6.2.1.1.

In order to further explore insights into the relationship between the SVD and PCA, let and be eigenvalues of the sample covariance matrix and the sample correlation matrix with their corresponding eigenvectors and , respectively. Also let , and be the singular values of , and with their corresponding singular vectors , and , respectively. The following relationships can be derived and summarized as follows.

1.

2. where is the squared root of the eigenvalue λ_j resulting from the fact that the sample correlation/covariance matrix R/K is the outer product of the data matrix with/out mean removed.

3. that implies that for each ju_j and v_j are either identical or differ by a sign. In the latter case, u_j and v_j point to complete opposite directions. However, it is the sign difference that distinguishes the SVD from PCA and makes both PCA and SVD two different transformations that also yield different performances. In order for SVD to avoid such a sign issue of which one, u_j or should be selected as the desired singular vector; we can map all data sample vectors on the singular vector u_j and sum all their projections by calculating their inner products via . If the total sum of the projections is non-negative, that is, is non-negative, the desired singular vector is set to u_j and otherwise, that is, if .

4. and for .

5. , which implies that for each j, and are either identical or differ by a sign. In the latter case, and point to complete opposite directions.

Finally, as an alternative, we can also find the singular values of the inner product matrix of the matrix , with size of . It turns out that both inner product matrix of , and the outer product matrix of , have the same identical non zero singular values with only difference in the number of zero singular values. This implies that to perform DR for any matrix , either inner product matrix or outer product matrix can be used for SVD. Apparently, in hyperspectral imaging the data sample correlation matrix that is a -scaled outer product matrix of a data matrix is the most intuitive and logical way to be chosen for DR.

There are also other factorization forms similar to (6.6) that can be used in place of SVD, for example, Cholesky decomposition, QR decomposition, and Householder transformation (Golub and Van Loan, 1989), that can be used for real-time implementation (see Chapter 33 and Chang (2013)).

6.2.2 Signal-to-Noise Ratio-Based Components Analysis Transforms

The PCA discussed in Section 6.2.1 is developed to arrange PCs in descending order of data variance. However, data variance does not mean image quality. In other words, PCA-ordered PCs are not necessarily ordered by image quality as shown by Green et al. (1988). In order to address this issue, Green et al. (1998) used an approach similar to PCA, called maximum noise fraction (MNF), that was based on a different criterion, signal-to-noise (SNR), to measure image quality. It was later shown by Lee et al. (1990) that MNF actually performed two stage processes, noise whitening with unit variance followed by PCA. Because of that MNF was also referred to as noise-adjusted principal component (NAPC) transform.

6.2.2.1 Maximum Noise Fraction Transform

The idea of MNF can be briefly described as follows. Assume that is a set of entire image pixel vectors in a hyperspectral image with size when n_r and n_c denote the number of rows and columns in the image, respectively. Let each image pixel vector also be denoted by an L-dimensional column vector . Suppose that the lth band image can be represented by an N-dimensional column vector, . It assumes that an observation model

(6.22)

where b_l is an observation vector, s_l is an N-dimensional signal column vector, and n_l is an N-dimensional column vector uncorrelated with s_l.

Let and denote the noise variance and signal variance of b_l, respectively. We define the noise fraction (NF) of the lth band image vector b_l to be the ratio of the noise variance, in the lth band image to the total variance, in the lth band image given by

(6.23)

where and .

Assume that w_l is an L-dimensional column vector that will be used to linearly transform the lth band image vector to a new lth band image described by via

(6.24)

It is worth noting that the ith component of the lth band image vector , in (6.24) is obtained by weighted sum over image pixels in all the L bands of the ith image pixel vector r_i. So, MNF is to find a transform specified by to maximize the NF defined by

(6.25)

Let be an MNF transform matrix such that where and . Then we can obtain the lth MNF-transformed band image by via specified by (6.24). Since the criterion of NF given by (6.23) can be re-expressed as

(6.26)

where is signal-to-noise ratio defined in (6.25). As a consequence, maximizing the NF_l specified by (6.23) is equivalent to minimizing SNR_l specified by (6.26). The Green et al. developed MNF is to find a set of to maximize the noise fraction in each of bands and then arrange MNF-transformed bands in descending order of maximum noise fractions according to (6.23) or in ascending order of SNR according to (6.26).

6.2.2.2 Noise-Adjusted Principal Component Transform

Recently, Lee et al. (1990) re-interpreted MNF transform and showed that MNF transform was nothing more than a two-stage process that first whitened noise variances of each band image to unit variance, then performed PCA transform on the noise-whitened band images. As a result, PCA-generated principal components can be arranged in the descending order of SNR that is the reverse order arranged by MNF transform. With this new interpretation, MNF is further referred to as noise-adjusted principal component (NAPC) transform. In other words, we can reinterpret MNF transform that maximizes the NF_l in (6.23) to minimize its reciprocal defined by

(6.27)

or maximize the SNR over the reciprocal of (6.26) defined by

(6.28)

As a result of (6.27) or (6.28), the obtained transform vectors arrange band images in ascending order of noise fractions or descending order of SNR. Interestingly, MNF used in the popular ENVI software is actually minimum noise fraction specified by (6.27).

The argument outlined above by (6.27) and (6.28) was based on Green et al.'s approach for each band image b_l, not an entire hyperspectral image cube. As noted, the lth MNF-transformed band image vector is obtained by (6.24) whose ith component is actually calculated by a weighted band correlation among the L bands within the ith image pixel vector via a particular weight vector w_l. It may not be conceptually clear and easy to be understood from a hyperspectral image viewpoint as an image cube. However, the connection between Green et al.'s MNF transform and Lee et al.'s NAPC can be better understood if a hyperspectral image is presented as a data matrix as follows. Following the same notations used in the MNF transform, assume that an L-band hyperspectral image has N image pixels denoted by with where n_r and n_c denote the number of rows and columns in the image, respectively. Also, let be an N-dimensional column vector that represents the lth band image of the hyperspectral image. Then the relationship between L-dimensional image pixel vectors r_i and L band images can be related by the following data matrix :

(6.29)

and

(6.30)

According to (6.29) and (6.30), Green et al.'s MNF transform performs on the left-hand side of (6.30) band-by-band images in a similar fashion as a remotely sensed image is stored by the Band SeQuential (BSQ) (Schowengerdt, 1997, p. 25). On the other hand, Lee et al.'s NAPC transform processes a hyperspectral image as the data matrix, that is, on the left-hand side of (6.29) in the same way as a remotely sensed image is stored by the band-interleaved-by-pixel (BIP) (Schowengerdt, 1997, p. 26). Therefore, in the NAPC transform, the sample data covariance matrix is obtained by and the noise covariance matrix, K_n is estimated from the data matrix X (Lee et al. 1990). A fast algorithm derived by Roger (1994) to implement NAPC transform is summarized as follows.

Algorithm for NAPC Transform

1. Find a whitening matrix F to orthonormalize K_n such that

(6.31)

where D_n is the diagonal variance matrix of K_n.

2. Find the resulting noise-adjusted data covariance matrix given by .

3. Find an eigenvector matrix resulting from PCA operating on K_adj, denoted by H such that

(6.32)

where D_adj is the diagonal variance matrix of K_adj.

4. Finally, the desired NAPC transform can be derived by

(6.33)

Now, let be the NAPC transform vectors obtained from Λ^NAPC in (6.33), that is, that is similar to (6.2). Then arrange band images in accordance with descending order of SNR.

According to (6.25) and (6.33), MNF transform and NAPC transform achieve DR by only retaining first q projection vectors and that correspond to the q largest SNRs

One major disadvantage of implementing MNF or NAPC transform is estimation of noise covariance matrix. Since it is based on the criterion of SNR, reliable noise estimation must be guaranteed. For details of estimation of noise covariance matrix we refer to Section 17.3 in Chang (2003a).