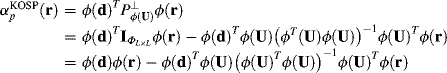15.2 Kernel-Based LSMA (KLSMA)
This section revisits and extends the three least squares-based techniques, OSP/LSOSP, NCLS, and FCLS, that have shown success in hyperspectral unmixing (Chang, 2003a) to their corresponding kernel-based counterparts, each of which represents three categories of techniques implementing LSMA. One is the category of abundance-unconstrained methods that include the well-known Gaussian maximum likelihood (GML) estimation and OSP, both of which have been shown essentially the same technique in Chapter 12. Another is the category of partially abundance-constrained methods, of which the NCLS method developed for constrained signal detection by Chang and Heinz (2000) is a representative. A third category of fully abundance-constrained methods among which the fully constrained least squares (FCLS) method developed by Heinz and Chang (2001) is the most widely used method for this purpose. So, when it comes to extend LSMA to kernel-based LSMA (KLSMA), it is natural to consider these three methods for kernel extension. The works in Kwon and Nasrabadi (2005b), Broadwater et al. (2007), and Liu and Chang (2009) are early attempts to accomplish this goal.
In what follows, we follow the work in Liu et al. (2012) to develop a unified kernel theory for extending LSMA to KLSMA by first developing the kernel-based LSOSP (KLSOSP) that is derived directly from the structure of the OSP. This KLSOSP is then used to derive a KNCLS that is in turn to be used to further derive KFCLS. It is our belief that this section provides most detailed derivations for kernel versions of the four LSMA, OSP, LSOSP, NCLS, and FCLS, including step-by-step algorithmic implementations.
15.2.1 Kernel Least Squares Orthogonal Subspace Projection (KLSOSP)
A kernel version of OSP was first derived in Kwon and Nasrabadi (2005b) for hyperspectral LSU. The idea is to use single value decomposition (SVD) to partition the undesired signature matrix U as 
so that 
in (2.78) or (12.3) can be decomposed and simplified to
where I is an 
identity matrix, B, C are orthogonal matrices, and D is a diagonal matrix. The purpose of (15.2) is to form dot products so that the kernel trick (Hofmann et al., 2008) can be applied without a need for performing matrix inversion. Since the used kernel mapping function is a positive-definite kernel, so is the output mapping matrix. As a result, the matrix resulting from the kernel trick should be in fact nonsingular and invertible. Using this fact, the kernel trick can be directly applied to 
specified by (15.2) without using SVD where 
is obtained from mapping 
in (15.2) into a feature space via a positive definite kernel and is always invertible. Consequently, a much simpler approach can be derived as follows.
First, let a nonlinear kernel be specified by ϕ. Then 
in (15.2) mapped into the feature space can be expressed as
Now, 
specified by (12.9) is mapped into a kernel version of OSP induced by ϕ in a feature space as
where 
in (15.3) is used to derive the second equality. It should be noted that the identity mapping 
in (15.4) can be simplified into 
based on the bilinearity properties from which each kernel function inherits according to Hofmann et al.'s work (Hofmann et al. 2008). That is,
Using (15.5) and the kernel trick described by
where K is a kernel function defined in the original data, (15.4) can be rewritten as
Since 
is obtained by a matched filter designed for signal detection not estimation, OSP is further extended to LSOSP (Tu et al., 1997) as abundance estimator as 
by including an abundance correction term, 
in 
as
(15.8) 
So, by taking advantage of (15.7) a kernel-based LSOSP (KLSOSP) can be further derived as
(15.9) 
which is not derived in Kwon and Nasrabadi (2005b).
15.2.2 Kernel-Based Non-Negative Constraint Least Square (KNCLS)
One of the major issues in implementing OSP is that it produces negative values for abundance fractions that are supposed to be non-negative. To mitigate this problem, ANC must be imposed as part of solving the optimization problem. An approach, called abundance NCLS, was recently developed by Chang and Heinz (2000). It minimizes an objective function, 
by constraining 
for 
. In doing so it introduces a Lagrange multiplier vector 
in the following constrained optimization problem:
where 
and cj for 
are constraints. With 
it follows that
and
Since there is no closed form that can be derived from (15.10), we ought to rely on a numerical algorithm for finding an optimal abundance vector 
for the abundance vector α that should iterate two equations specified by (15.11) and (15.12) while satisfying the following Kuhn–Tucker conditions:
(15.13) 
where P and R represent passive and active sets that contain indices representing negative or positive abundances, respectively. By replacing dot products in (15.11) and (15.12) using kernel tricks (15.6), 
can be derived by
and
Since 
can be considered as kernel LSOSP estimator and αKLSOSP(r) specified by
KNCLS actually makes use of KLSOSP as its initial guess to iterate two equations (15.14) and (15.15) to find its final KNCLS solution as follows.
KNCLS algorithm:
and active set 
, that is, empty set. Let 
.
and let 
.
are positive, the algorithm is terminated. Otherwise, continue.
.
that correspond to negative components of 
to 
and the resulting index sets are denoted by 
and 
, respectively. Create a new index set 
and set it equal to 
.
denote the vector consisting of all components 
in 
.
by deleting all rows and columns in the matrix 
that are specified by 
.
. If all components in 
are negative go to step 15. Otherwise, continue.
and move the index in 
that corresponds to 
to 
.
, as shown in step 8, with the new 
and 
index sets.
by deleting every column of 
specified by 
.
.
in 
are negative, then move these components from 
to 
. Go to step 6.
by deleting every column of 
specified by 
.
. Go to step 3.
15.2.3 Kernel-Based Fully Constraint Least Square (KFCLS)
According to Heinz and Chang (2001) one simple approach to implementing ASC in conjunction with ANC is to introduce a new signature matrix N and an auxiliary vector s into the NCLS with
where 
is a p-dimensional vector and 
controls the rate of convergence for FCLS algorithm. By replacing the M and r in KNCLS with modified signature matrix N and the new vector s in (15.17), respectively, a KFCLS algorithm can be derived as follows.
KFCLS algorithm:
and active set 
, that is, empty set. Let 
.
and let 
.
are positive, the algorithm is terminated. Otherwise, continue.
.
that correspond to negative components of 
to 
and the resulting index sets are denoted by 
and 
, respectively. Create a new index set 
and set it equal to 
.
denote the vector consisting of all components 
in 
.
by deleting all rows and columns in the matrix 
that are specified by 
.
. If all components in 
are negative go to step 15. Otherwise, continue.
and move the index in 
that corresponds to 
to 
.
, as shown in step 8, with the new 
and 
index sets.
by deleting every column of 
specified by 
.
.
in 
are negative, then move these components from 
to 
. Go to step 6.
by deleting every column of 
specified by 
.
. Go to step 3.
As a concluding note, the KNCLS and KFCLS presented above are also independently derived in Broadwater et al. (2007) and later published in Camps-Valls and Bruzzone (2009) as a book chapter where the KNCLS was only used as a means of deriving the KFCLS and was not used in their experiments at all. In addition, many details presented here are not available in these two references.
15.2.4 A Note on Kernelization
The key idea of kernelization is the use of the kernel trick that has not been really clarified in many reported efforts when it is used. As a consequence, there is always confusion. As an example, support vector machine (SVM) is originally developed as a binary classifier to find a hyperplane maximizing the distance between support vectors in two separate classes and has nothing to do with kernelization. The introduction of kernelization into SVM allows SVM to make linear decisions in a feature space to resolve linear nonseparability problems. As a matter of fact, SVM used in the literature is indeed kernel-based SVM (KSVM) not SVM without using kernel. In general, there two ways to use the kernel trick to perform kernelization. One is to kernelize a transformation to map all data samples in a high-dimensional feature space. Examples of this type include kernel-based principal components analysis (PCA) and kernel-based RX detector, both of which require all data samples for kernelization of the sample covariance matrix. The advantage of this approach is no prior knowledge is needed since all data sample are involved for kernelization. But its major disadvantage is computational complexity which is exceedingly expensive. Unfortunately, most of the reported research efforts along this line have avoided addressing this issue. To mitigate this dilemma, an alternative approach is to use a specifically selected of data samples to perform kernelization such as kernel-based Fisher's linear discriminant analysis and KSVM. Consequently, the computational complexity is reduced to that required to perform kernelization only on these selected samples. However, this also comes with a price of how to judiciously select data samples for kernelization. This is a very challenging issue. A third approach is the approach proposed in this chapter which kernelizes a classifier instead of training samples. More specifically, KLSMA only kernelizes the signatures used by OSP, LSOSP, NCLS, and FCLS that are used to perform spectral unmixing where these signatures are provided a priori not necessarily training samples. This is quite different from existing kernel-based techniques as described above which operate entire data samples or training samples to be mapped into a high dimensional feature space. More importantly, the computational cost saving is tremendous because the number of the signatures kernelized by KLSMA is generally very small compared to other kernel-based methods which requires a large number of training samples such as SVM or Fisher's linear discriminant analysis or the entire data samples such as PCA.