33.2 Endemember Extraction
Endmember extraction has received considerable interests in recent years. This is mainly because with very high spectral resolution provided by hundreds of contiguous spectral bands hyperspectral sensors are capable of extracting many unknown and subtle signal sources which cannot be generally resolved by multispectral sensors. One of such signal sources is endmembers which provides crucial and vital information in data exploitation. Particularly, endmembers can be used to specify spectral classes present in the data. According to the definition in Schowengerdt (1997), an endmember is an idealized, pure signature for a class. So, technically speaking, an endmember is a signature generally available in a spectral library or database, and it is not necessarily a data sample vector present in the data. With this clarification, a pure data sample vector is specified by an endmember, but may not be the other around. Unfortunately, in real applications pure data sample vectors probably never exist because they may be contaminated by many unexpected effects resulting from noise, clutters, unknown interferers, etc. Accordingly, when an endmember extraction algorithm is applied to real data, it intends to find those data sample vectors which are most likely pure and represent endmembers. In unsupervised LSMA (ULSMA) discussed in Chapter 17, such data sample vectors are referred to as virtual signatures (VSs) and can be found by an unsupervised algorithm to be used for spectral unmixing.
Due to the nature of purity in endmembers, convexity geometry has been a key notion to design algorithms to find endmembers. An earliest attempt was reported by Boardman (1994) who used OP to develop one of best known endmember extraction algorithms, pixel purity index (PPI). Since there is no prior knowledge that can be used to find endmembers, its idea uses a set of randomly generated unit vectors, to be called skewers, to point to as many different projection directions as possible. All data sample vector are then orthogonally projected on each of these skewers where the maximal or minimal projection on each skewer can be calculated. For each data sample vector, a PPI count can be produced by counting many skewers on which this particular data sample vector has either maximal or minimal projection. By adaptively thresholding PPI counts obtained for all data sample vectors, a set of candidates for endmembers can be generated and further used to extract a desired set of endmembers by human intervention. To alleviate the random nature caused by using skewers resulting from PPI and human intervention, Chang and Plaza (2006) developed an initialization-specified PPI where an endmember initialization algorithm, ATGP was used to generate a specific set of initial skewers and Chang et al. (2010) took a complete opposite direction by considering PPI as a random algorithm where the result produced by PPI using one set of random initial skewers is considered as a realization of such a random algorithm.
Another attempt deviated from using of OP was made by Ifarraguerri and Chang (1999) who appealed for the concept of positive convex cone to satisfy abundance non-negativity constraint (ANC) imposed on endmembers and then searched for a set of data sample vectors with maximal convex cone volume within the data space. The vertices of the found convex cone are the desired endmembers. Since then several similar ideas using the concept of non-negative matrix factorization (NMF) developed in Lee and Seung (1999) were further explored for endmember extraction, for example, the work by Pauca et al. (2006).
A third attempt was reported by Craig (1994) who proposed a minimal volume transform (MVT)-based approach to satisfy both ANC and abundance sum-to-one (ASC) imposed on endmembers to find a set of data sample vectors that forms a simplex with minimal volume which includes all the data sample vectors. The MVT criterion has played a key role in the development of NMF-based minimal volume constrained non-negative matrix factorization (MVC-NMF) developed by Miao and Qi (2007), and linear programming-based minimal volume enclosing simplex (MVES) was developed by Chan et al. (2009).
A fourth attempt was further made by Winter who developed an N-finder algorithm (N-FINDR) (Winter, 1999a, 1999b, 2004). It is very similar to MVT. But instead of minimizing simplex volume it maximizes the volumes of simplexes that are embedded in data sample space. In other words, Craig deflated simplexes that contain all data sample vectors until it reaches a simplex with minimal volume, whereas Winter took an opposite approach by inflating simplexes embedded in data space until it reaches a simplex with maximal volume. Up to now the concept of the Winter approach is probably the most widely used criterion in the literature to design an endmember extraction algorithm due to its close tie with spectral unmixing. Therefore, it is interesting to provide a little history for an evolution of the N-FINDR development over the past years.
Since the Winter N-FINDR was first proposed (Winter, 1999a, 1999b, 2004; Winter and Winter, 2000), many efforts have been devoted to improving this algorithm in the sense of computational efficiency. According to Winter's criterion finding a simplex of maximal volume should exhaust all possible simplexes. While such an exhaustive search is nearly impossible in practice, two approaches have been investigated in the past. One is to grow simplexes one vertex after another such as the simplex growing algorithm (SGA) developed Chang et al. (2006). The other is modifications of the Winter algorithm in terms of implementing N-FINDR sequentially similar to the one developed in Winter (2004) which implements two iterative loops with the outer loop iterated for data sample vectors and the inner loop iterated for endmember replacement. Many improved N-FINDR algorithms reported in the literature belong to the latter category which uses such a sequential Winter N-FINDR as a base to develop different variants (Plaza and Chang, 2005, 2006; Wu et al., 2008; Chowdhury and Alam, 2007; Zortea and Plaza, 2009; Dowler and Andrews, 2011; Du et al., 2008a, 2008b; Wang et al., 2009). One major approach is to modify the algorithmic structure used in the sequential Winter N-FINDR. An earliest attempt was made in Plaza and Chang (2005) and Plaza and Chang (2006) where an algorithm was specifically laid out to fill in missing details in Winter (1999a, 1999b) to implement a different version of sequential N-FINDR. It was then followed by various versions developed by Wu et al. (2008), Chowdhury and Alam (2007), Zortea and Plaza (2009), and Dowler and Andrews (2011). With an interesting twist of swapping two loops in the Winter N-FINDR (2004), that is, making the inner loop an outer loop and the outer loop an inner loop, Wu et al. (2008) derived another version of the sequential Winter N-FINDR algorithm, called SuCcessive N-FINDR (SC N-FINDR). Unfortunately, the work in Wu et al. (2008) was not referenced in Du et al. (2008a, 2008b) and Wang et al. (2009) where their developed algorithms either identical or very close to the SC N-FINDR.
While many N-FINDR developers have placed their focus on sequential implementation of N-FINDR (Winter, 1999a, 1999b, 2004; Winter and Winter, 2000; Chowdhury and Alam, 2007; Zortea and Plaza, 2009; Dowler and Andrews, 2011; Du et al., 2008a, 2008b; Wang et al., 2009), the issue of using initial conditions in N-FINDR has been overlooked. This is in fact a serious problem with reproducibility of final selection of endmembers since N-FINDR produces different final results if different sets of random initial conditions are used. Three ways have been suggested to resolve this issue. One is to use an endmember initialization algorithm (EIA) to generate an appropriate set of initial endmembers such as automatic target generation (ATGP) in Plaza and Chang (2005). Another is real-time N-FINDR processing developed in Wu et al. (2010) which takes the first p input data sample vectors as initial endmembers. A third one is random N-FINDR proposed in Chang et al. (2009), Wu (2009), and Chang et al. (2011), which considered N-FINDR as random algorithm to repeatedly implement N-FINDR with different sets of random initial endmembers until a stopping rule is met.
According to the algorithmic structure implemented in IN-FINDR developed in Section 7.2.3.2, the inner loop is indeed a two-loop sequential process with one loop iterating N data sample vectors for each a given fixed endmember position and the other loop iterating p endmember positions, which is the number of endmembers, while the outer loop simply iterates another new set of endmembers found by the inner loop in a previous iteration. So, in order to make such an implementation more clearer and attractive Xiong et al. (2011) revisited IN-FINDR and separated the inner loop implemented in the IN-FINDR from its outer loop to have it implemented as a stand-alone algorithm, referred to as SeQuential N-FINDR (SQ N-FINDR). By virtue of this new defined SQ N-FINDR, IN-FINDR can be re-implemented in a broader sense as a three-loop (outermost, outer, and inner loops) sequential process where the outermost loop is used to iterate a new initial set of p endmembers generated by the outer loop; the outer and inner loops are designed to iterate data sample vectors and endmember positions separately. When the inner loop iterates p endmember positions and the outer loop iterates N data sample vectors, it is called the SQ N-FINDR. When these two loops are reversed, the resulting two-loop process is called SC N-FINDR. As a result, in analogy with SC N-FINDR, the performance of SQ N-FINDR is also heavily determined by its used initial conditions. In this case, in order to mitigate this random issue, they can be jointly implemented with the outermost loop carried out in IN-FINDR, respectively. The resulting IN-FINDR algorithms are referred to as iterative SQ N-FINDR (ISQ N-FNDR) and iterative SC N-FINDR (ISC N-FINDR). With this interpretation/IN-FINDR developed in Section 7.2.3.2 is in fact the ISQ N-FINDR which is identical to the sequential N-FINDR in Wu et al. (2008) as well as the IN-FINDR referred in Chang et al. (2009), Wu (2009), and Xiong et al. (2011), all of which include a third loop to implement SQ N-FINDR or SC N-FINDR repeatedly by taking final set of endmembers generated in the previous run as a new set of initial conditions for next run. To the author's best knowledge, many algorithms designed to implement N-FINDR in the literature can be considered to be either identical or equivalent to SQ N-FINDR, SC N-FINDR, or IN-FINDR one way or another. Interestingly, it is believed that IN-FINDR remains the only one which has never been explored in the literature except those in Wu et al. (2008), Chang et al. (2009), Wu (2009), and Xiong et al. (2011) and is yet to be explored in the future. More details can be found in Chang (2013).
Several dilemmas resulting from implementing N-FINDR described above have led to the development of SGA which finds p endmembers by growing simplexes one vertex at a time where each new endmember is specified by a newly added vertex that yields the maximal volume of simplexes being considered (Chang et al., 2006). As we recall in Section 7.2.3.3, where a multiple-replacement version of IN-FINDR, referred to as s-IN-FINDR, is developed the number of endmembers needed to be replaced in each iteration is set to s. When s = 1, it is reduced to the single-replacement IN-FINDR. On the other hand, when s = p, s-IN-FINDR becomes the original version of N-FINDR. So, this idea can be also carried over to generalize SGA to s-SGA where the number of initial endmembers needed to start with SGA is set to s. In this case, implementing s-SGA requires two-stage processes. The first-stage process is to find a set of s initial endmembers that maximizes volumes of s-simplexes to initialize SGA, and the second-stage process is to grow and find the maximal simplex volume starting from an (s + 1)-simplex to a p-simplex. Using this generalization, when s = 1 and 2, s-SGA is reduced to 1-SGA and 2-SGA as described in Section 8.3 and Figure 8.1. As a consequence, the computational complexity of implementing s-SGA is the sum of computational costs of two-stage processes, that is, computation complexity of finding an optimal set of s initial endmembers plus computational complexity of finding growing simplexes with maximal volumes starting from the number of vertices, s + 1 to p. As s is increased, the heavy computational load begins to shift from finding growing simplexes with maximal volumes to finding an optimal set of s initial endmembers. When it reaches p, that is, ![]() , no process of growing simplexes is needed and the entire computational cost is completely determined by finding an optimal set of p initial endmembers. In this case, p-SGA becomes the original version of N-FINDR, which can be considered as a special case of s-SGA with s set to p.
, no process of growing simplexes is needed and the entire computational cost is completely determined by finding an optimal set of p initial endmembers. In this case, p-SGA becomes the original version of N-FINDR, which can be considered as a special case of s-SGA with s set to p.
The three design rationales, OP, convex cone, and simplex described above are main trends for designing and developing endmember extraction algorithms. Interestingly, these three are actually derived from three versions of how to implement LSMA discussed in Chang (2003a) which are abundance-unconstrained LSMA, least squares OSP (LSOSP), ANC-constrained constrained least squares (NCLS) (a partially abundance-constrained LSMA), and (ANC,ASC)-constrained fully constrained least squares (FCLS) (fully abundance-constrained LSMA). So, it is not a surprise to see that the least-squares error (LSE) used as a criterion for spectral unmixing performed by LSMA can also be used as a design criterion to find endmembers where three LSE-based endmember extraction algorithms corresponding to LSOSP, NCLS, and FCLS can also be developed, unsupervised LSOSP (ULSOSP), unsupervised non-negativity constrained least squares (UNCLS) by Chang and Heinz (2000), iterative error analysis (IEA) by Neville et al. (1999), and unsupervised fully constrained least squares (UFCLS) by Heinz and Chang (2001) as their three respective representatives. All these discussions can be found in Chapter 8. According to the studies in Chang et al. (2010) and Chapter 11, the use of maximal simplex volume as a criterion is among best criteria for extracting endmembers. This makes sense from a view point of linear convexity where two constraints, ASC and ANC must be satisfied, while the OP does not satisfy any one of these two constraints. Interestingly, the convex cone-based approach such as VCA actually implements the OP criterion with ANC. As a result, in general, VCA does not perform as good as N-FINDR. However, for a convex cone to also satisfy the ASC the convex cone analysis (CCA) developed by Ifarraguerri and Chang (1999) was designed for this purpose. This similarity can also be found in LSMA where the abundance-unconstrained LSOSP, ANC-constrained NCLS and (ASC,ANC)-constrained FCLS can be considered as respective counterparts of PPI, ANC- constrained convex cone-based VCA, and (ASC,ANC)-constrained simplex-based N-FINDR. More details on endmember extraction from this perspective will be explored in Chang (2013).
Since the above-mentioned approaches, PPI, CCA, and MVT/N-FINDR are developed for finding all the endmembers simultaneously at once, their computational complexity is generally very high and expensive, particularly, for CCA and MVT/N-FINDR. To mitigate and alleviate this computational problem, two approaches have been investigated. One is to make endmember extraction a two-iterative sequential process instead of a simultaneous process. Examples include IN-FINDR, SC N-FINDR, Miao and Qi (2007), Wu et al. (2008) and Chan et al. (2009) and most recently, SQ N-FINDR in Chang et al. (2011). A second approach is to grow endmembers one at a time until it reaches the desired number of endmembers. In this regard, OP-based ATGP (Ren and Chang, 2003), convex cone-based vertex component analysis (VCA) (Nascimento and Dias, 2005), and simplex-based SGA (Chang et al., 2006) are developed for this purpose where ATGP, VCA, and SGA represent three categories of abundance constraints, no abundance constraint corresponding to OP, ANC corresponding to convex cone and both ANC and ASC corresponding to simplex. Tables 33.1 and 33.2 with their corresponding counterparts of block diagrams depicted in Figures 33.1 and 33.2 summarize relationships among algorithms developed based on three design criteria, OP, convex cone, and simplex plus LSE as well as how to find endmembers simultaneously or one after another by growing endmembers sequentially.
Figure 33.1 Relationships among LSE-based endmember extraction algorithms.

Figure 33.2 Relationships among convexity-based endmember extraction algorithms.
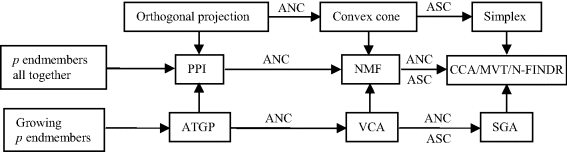
Table 33.1 Least squares (LS)-based endmember extraction algorithms.
| Constraints | How to find endmembers | Algorithms |
| No constraint | Growing endmembers | ULSOSP |
| ANC | Growing endmembers | UNCLS |
| ANC, ASC | Growing endmembers | IEA/UFCLS |
Table 33.2 Categories of endmember extraction algorithms using convexity geometry as a criterion.

As recalled in PART II (Chapters 7–11) in this book, endmember extraction algorithms (EEAs) are treated on the basis of algorithmic implementation, viz. SiMultaneous EEAs (SM-EEAs), SeQuential EEAs (SQ-EEAs), initialization-driven EEAs (ID-EEAs), and random EEAs (REAAs). Tables 33.1 and 33.2 and Figures 33.1 and 33.2 provide another categorization of endmember extraction a which will be discussed in great detail in Chang (2013) which is based on various abundance constraints imposed on algorithms according to the abundance constraints imposed on EEAs from abundance-unconstrained OP-based EEAs, partially abundance-constrained convex cone-based EEAs and fully abundance-constrained simplex-based EEAs.
In addition to criteria described above, OP, linear convexity, and LSE, there is a fourth criterion that can be used to find endmembers. It considers endmembers as statistically independent random signal sources where mutual information is the criterion to be used to identify endmembers. The first work reported in the literature is the one developed by Wang and Chang (2006b), referred to as ICA-based SQ-EEA discussed in Section 8.6.5. However, the abundance vectors blindly separated by ICA are not necessarily positive signal sources. To address this need, Oja and Plumbley (2004) developed an approach to finding positive abundance vectors that satisfy the ANC. Nevertheless, it should be noted that such an approach does not satisfy the ASC. Otherwise, the separated sources will not be statistically independent.
As a final comment on endmember extraction, it has been misleading using various terminologies to represent endmember extraction. As a matter of fact, endmember extraction, endmember selection, and endmember determination are all completely different concepts. First, endmember extraction is a task to extract signatures which are supposed to be endmembers in the data without prior knowledge, while endmember selection is performed by singling out a set of potential endmember candidates which are supposed to be known a priori. In general, it is a follow-up task of endmember extraction. On the other hand, endmember determination is to determine whether a given signature is an endmember. It does not perform endmember extraction or endmember selection. Instead, it generally requires performing linear spectral unmixing (LSU) to determine if a given set of signatures used for unmixing are endmembers. It may be a main reason why endmember extraction is confused with linear spectral unmixing. In his 1999's paper (1999b), Winter proposed an autonomous spectral endmember determination where the knowledge of endmember as not provided. To resolve this issue, Winter develops endmember “finding” (Note: not endmember “extraction”) via the so-called N-finder algorithm to first find potential endmember candidates using maximal simplex volume as a criterion and then further performs LSU determine whether the found potential endmember candidates are indeed endmembers. So, basically, Winter did not use LSU to find endmembers, but rather used it to determine endmembers. However, since a simplex also satisfies ASC and ANC, LSMA has been also used as a means of extraction endmembers such as iterative error analysis (Neville et al., 1999) and unsupervised fully constrained least squares (UFCLS) (Heinz and Chang, 2001). But it does not imply that endmember extraction must be implemented in conjunction with LSU or considered as a LSU technique. As a matter of fact, as shown in Chang et al. (2010) where five different criteria were investigated, using LSMA may be effective but may not be as good as maximal simplex volume for endmember extraction. On the other hand, as also shown in Chang et al. (2010), signatures used for LSU are not necessarily pure signatures as endmembers and can be mixed signatures. This provides further evidence that endmember extraction and LSMA are indeed separate techniques designed for different tasks. So, performing LSU is not a part of endmember extraction. However, when LSU is performed in an unsupervised manner when no prior knowledge of endmembers is available, endmember extraction can always be used as a preprocessing step to find potential endmembers which will be later determined by the follow-up LSU, which can be considered as a similar approach proposed by Winter's N-FINDR. Accordingly, LSU and endmember extraction can be benefited by each other.
