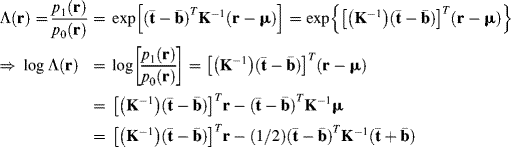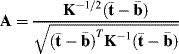2.2 Subsample Analysis

The most fundamental task in subsample analysis is subsample detection where two types of detectors will be discussed in this section, detectors with hard decisions and detectors with soft decisions, which correspond to pure-sample target detector and subsample target detector, respectively.

2.2.1 Pure-Sample Target Detection

Despite that a subsample target may be present in a sample, the pure-sample target detection is performed by forcing a detector to make a binary decision, whether the sample is to be detected as target sample or not. In other words, the pure-sample target detection can only say “yes” if target is detected and “no” if target is absent. So, even though a subsample target does not fully occupy the entire sample, it must be claimed to be a pure target sample if a detector says “yes” as target is detected. To emphasize such a nature, the commonly used binary hypotheses-based detectors described in the following are called pure-sample target detectors.

A classical approach to pure-sample target detection is to formulate a signal detection problem as the following binary hypothesis-testing problem.

(2.1)

where r is an observable random variable; the null hypothesis H₀ and alternative hypothesis H₁ represent the case of target absence and the case of target presence with their probability distributions specified by P₀(r) and P₁(r), respectively. A decision rule δ(r) for H₀ versus H₁ specified by (2.1) is a partition of the observation space Γ into two regions: Γ₁ referred to as rejection region and Γ₀ referred to as acceptance region. By virtue of the defined Γ₀ and Γ₁ with , the decision rule δ(r) is generally described by

(2.2)

and is shown in Figure 2.1.

Now, a solution to (2.2) is to find a best partition in some optimal sense. Specifically, we introduce a cost function specified by a cost matrix where c_ij is the cost of the decision saying H_i when H_j is actually true and a risk function of the decision rule δ(r) under hypothesis H_j, R_j(δ) given by

(2.3)

Suppose that the prior probabilities of H₀ and H₁ for (2.1) are specified by π₀ and π₁, respectively. The averaged risk r(δ) is then defined by

(2.4)

Minimizing (2.4) over all possible decision rules yields the Bayes detector δ^Bayes(r) given by

(2.5)

The detector of this type can be considered as pure sample-based signal detection. If we further assume that the probability distributions P₀(r) and P₁(r) have their own probability density functions given by p₀(r) and p₁(r), then . It can be shown in Poor (1994) that the solution to (2.5) can be

(2.6)

where Λ(r) is the likelihood ratio test (LRT) given by p₁(r)/p₀(r) and the threshold τ is given by . It should be noted that the Bayes detector in (2.6) declares H₁ when the LRT Λ(r) equals the threshold τ. While this is generally true, it is not necessarily correct, particularly when the random variable r is not continuous, but discrete. In order to address this issue, let and Figure 2.1 becomes Figure 2.2, where and κ is the probability that H₁ is true when Λ(r) is equal to the threshold τ.

The risk function (2.3) can be further modified as

(2.7)

As a result of (2.7) the Bayes rule in (2.6) becomes a randomized detector δ^Bayes(r) specified by the following form:

(2.8)

It is worth noting that it is the threshold τ that determines which type of a detector will be. When τ is completely specified by a cost function and prior probabilities of H₀ and H₁ as the case of (2.3) and (2.4), the detector is a Bayes detector. When the τ is only specified by a cost function with no knowledge of prior probabilities of H₀ and H₁, the detector is a minimax detector. A most practical case is that there is no knowledge about the cost function or prior probabilities of H₀ and H₁. Under such circumstances, the τ is determined by a prescribed false alarm probability, P_F and the resultant detector becomes a well-known detector, called Neyman–Pearson (NP) detector. More specifically, for a detector, δ let P_F(δ) be the false alarm probability given by

(2.9)

and P_D(δ) be the detection probability or detection power given by

(2.10)

The NP detector is one, denoted by δ^NP(r) to solve

(2.11)

where β is known as the significant level of test. In order to evaluate the detection performance of δ^NP(r), a receiver operating characteristic (ROC) curve is plotted as a function of P_D versus P_F for analysis (more details can be found in Chapter 3). Interestingly, no matter which detector is derived as above, the structure of the detector always turns out to be the LRT. In other words, all the Bayes, minimax, or Neyman–Pearson detectors end up with the same form of LRT. Details of signal detection theory can be found in Poor (1994).

As mentioned earlier, in many cases where the probability distributions p₀(r) and p₁(r) are continuous such as Gaussian distributions, the detector δ^Bayes(r) in (2.8) can be always made a deterministic detector, δ(r) by setting κ = 1 with no effect on detection performance. In this case, (2.8) can be simplified and reduced to (2.6).

The hypothesis-testing problem described by (2.1) is a general setting for a detection problem where no signal model is assumed. However, if (2.1) is considered for signal detection in noise, the hypothesis-testing problem (2.1) can be specifically represented by

(2.12)

where s is the signal of interest and n represents an additive noise. Of particular interest is the case that the noise in (2.12) is Gaussian in which case the Bayes decision rule (2.6) becomes a well-known matched filter with the matching signal specified by the signal s.

2.2.2 Subsample Target Detection

In order to apply the signal detection model (2.12) to subsample target detection, we assume that a subsample target signal specified by signature t is embedded in the background b with their proportions specified by α and 1 − α, respectively, where the proportion α will be referred to as abundance fraction of t. As a result, the signal s in (2.12) will be replaced by a subsample target signal t with its proportion occupied in r specified by an abundance fraction, α mixed with its background signature b with the abundance fraction, 1 − α, that is, . The signal detection model in (2.12) becomes

(2.13)

Using (2.13) subsample target detection is performed by the LRT given by

(2.14)

Unlike pure sample-based signal detection specified by (2.12) using a threshold τ, the LRT, Λ(r), in (2.14) detects the subsample target t by estimating the abundance fraction of t, α present in r. Since the amount detected by a detector specified by LRT is proportional to the abundance fraction of α contained in the sample r, LRT essentially serves as an estimator of α, where the r is included in to indicate the dependency of the abundance estimate on the r. By virtue of (2.14), a subsample target detector can be interpreted as a detector that makes a soft decision based on its estimated abundance instead of the one in (2.6) or (2.8) that makes a hard decision based on a threshold τ. The detector of this type can be considered as subsample signal detection with soft decisions via the estimation of abundance fraction α, through r as opposed to pure sample-based signal detection with hard decisions determined by the threshold τ. A similar concept will also be explored in Sections 2.3.1 and 2.3.2.

Since the major focus of subsample analysis is on the subsample target of interest t, the background b is generally not known and is something we would like to remove or suppress in order to improve detectability of the t. In doing so, two general approaches have been proposed in the past. One is to obtain the background knowledge from a secondary data set originally proposed by Kelly (1986), and the other is to extend a model in (2.13) to a signal-background-noise (SBN) model proposed in Thai and Healey (2002) and signal-decomposed and interference/noise (SDIN) model suggested in Du and Chang (2004).

2.2.2.1 Adaptive Matched Detector (AMD)

As a special case of (2.12) where both probability density functions p₀(r) and p₁(r) are Gaussian distributions specified by and with the same covariance matrix K and the background mean, and target mean, , respectively, (2.14) becomes

(2.15)

Because does not depend upon the observation r and can be absorbed in the threshold τ in (2.8) to produce a new threshold defined by

(2.16)

we can define a detector δ^AMD(r), called adaptive matched detector (AMD) via (2.15) to estimate the abundance α by

(2.17)

which is a matched filter with the matching signal specified by . However, is actually the difference between two whitened means by the covariance matrix K; the matching signal is simply the difference of two means after the data is whitened. If we calculate the variances of the detector of (2.17) under each of two hypotheses, H₀ and H₁ in (2.13), by

(2.18)

their variances turn out to be identical and are independent of hypotheses. Most interestingly, the variance specified by (2.18) is actually the Mahalanobis distance between background mean and target mean.

If we further use (2.18) to normalize AMD in (2.17), the resulting detector is referred to as normalized AMD (NAMD), δ^NAMD(r) and given by

(2.19)

which becomes the commonly used adaptive matched filter. It should be noted that using the variance in (2.18) as a scaling constant in (2.19) has significant impact on the estimation of α. It has been shown in Chang (1998) and Chang (2003a) that it was this constant to correct estimation error of α. Unfortunately, this constant has been generally referred to as a normalization constant in the literature, which is somewhat misleading. So, in order to further estimate the abundance of α in (2.13) more accurately, we let as an abundance estimator and use it as a detector given by

(2.20)

where is a new threshold obtained by absorbing the constant into the threshold defined in (2.16) with τ defined in (2.8).

An alternative approach to arriving at the same detector in (2.20) is to perform a whitening process on the original data by implementing a linear transformation specified by

(2.21)

where A is referred to as a whitening matrix defined by

(2.22)

As a result of (2.22), the transformed data have zero mean and variance normalized to unity where the standard deviation of (2.18) used as the denominator in (2.21) to normalize the original data r has the same effect as does the variance in (2.18) used to normalize the detector in (2.19).

In many real applications the statistics of the noise n, K and the knowledge of the background mean in (2.20) are generally not known in advance. This implies that both the detector and the threshold τ″ in (2.20) cannot be specifically characterized. As a result, the hypothesis-testing problem specified by (2.13) is no longer a simple binary hypothesis-testing problem, but rather a binary composite hypothesis-testing problem where a uniformly most powerful (UMP) detector is sought to optimize detection performance. Unfortunately, such a UMP detector generally does not exist. A general approach is to extend LRT, Λ(r), in (2.20) to so-called generalized LRT, which leads to a maximum likelihood detector. In order to solve GLRT, a common assumption made on the noise is Gaussian so that the maximum likelihood detector can be derived. On the other hand, since the cost function and priorities of each hypothesis are also not unknown, the threshold τ used in (2.20) cannot be determined. To resolve this issue, an NP detector is implemented for this purpose. However, as noted, the performance of an NP detector is determined by a compromise between P_D and P_F via the ROC analysis. If an NP detector is designed to perform a UMP detector while its false alarm probability is retained at a constant level, such a detector is called constant false alarm rate (CFAR) detector, which has been widely used in radar and sonar signal processing. On the other hand, in order to obtain the background knowledge , a secondary data set is also needed to produce required information. Many efforts along with this approach have been reported in the literature, Reed et al. (1974), Kelly (1986), Reed and Yu (1990), Manolakis and Shaw (2002), and so on.

2.2.2.2 Adaptive Subspace Detector (ASD)

The AMD-based subsample target detection discussed in Section 2.2.2.1 follows the standard Neyman–Pearson detection theory by finding GLRT or CFAR detector where the probability distribution under each hypothesis and background knowledge such as noise must be known a priori, preferably Gaussian distributions from which a GLRT can be derived and an ROC analysis can be further used for detection performance. As a matter of fact, in reality, such assumptions are generally not true for hyperspectral imagery, despite the fact that CFAR- or GLRT-based approaches seem to perform successfully in subsample analysis. So, it is interesting to find out how can an approach perform well, while its assumptions violate practical constraints? This question will be answered by the following approach.

As noted, AMD assumes that noise or background statistics are given a priori. In this section, we consider an alternative approach modified from the subspace detector proposed by Kraut et al. (2001), which can be also considered as a CFAR detector. It only assumes subsample target knowledge without knowing noise/background statistics. It is also referred to as adaptive subspace detector (ASD) due to the fact that it is derived from the concept of subspace projection. However, it is worth noting that the ASD derived here is a little bit different from ASD in Kraut et al. (2001) in the sense that no signal model such as (2.13) in Kraut et al. (2001) is assumed and involved in our derivation. The only assumption made is the prior signature knowledge of the subsample target, t. ASD derived in (2.28) is nearly identical to CEM derived in (2.33) except the sample covariance matrix used in ASD is replaced by the sample correlation matrix in CEM.

According to Kraut et al. (2001), it first uses the sample covariance matrix, K, to whiten the data and is then followed by a subspace projection approach that projects the entire whitened data space into two separate mutually orthogonal linear subspaces, called signal subspace, denoted by and its orthogonal subspace, referred to as clutter space, denoted by via two orthogonal subspace projection operators specified by and defined as follows.

(2.23)

Now, let be the whitened vector of any weighting vector, w and the signal-to-clutter ratio (SCR) be defined by

(2.24)

Maximizing (2.25) over w is equivalent to finding a vector w minimizing

(2.25)

which is in turn equivalent to finding an optimal vector w that maximizes

(2.26)

Using Schwarz's inequality and following the same argument as (2.6) in Chang (2003a, p. 42), the solution to maximization of (2.26) or (2.24) denoted by can be shown to be

(2.27)

where κ is any constant. Using the weight obtained in (2.27) by letting , we can define an adaptive subspace detector, δ^ASD(r) on the original data space by

(2.28)

where is a scaling constant and is a very important factor in correcting estimation error of the abundance fraction of the subsample target t (Chang, 1998).

It is worth mentioning that the SCR defined in (2.24) is slightly different from signal-to-noise ratio (SNR) generally used in signal detection in noise in the sense that the clutter considered in (2.24) may include unwanted signals such as background or interferers that can be treated as structure noise compared to the noise considered in SNR that is assumed to be a random noise and can be viewed as an unstructured noise. Since a subsample target is embedded in a sample specified by its abundance fraction α to reflect its spatial presence, the spatial proportion accounted for background is (1 − α). In this case, using SCR is more appropriate than using SNR for subsample target detection.

Comparing (2.28) against (2.19), the t and the constant κ in (2.28) play the same role as and do in (2.19). However, as noted in AMD, a secondary data set is needed to estimate the background so that the background mean can be removed. In addition, since there is no Gaussian assumption made on the data, target signal in assumed in (2.12) can be replaced by the target signal of interest t. With set to zero and set to t, the specified by (2.19) is reduced to δ^ASD(r) in (2.28).

Extensions of ASD from the standard signal detection model in (2.13) to a more general model have been investigated in recent years, such as the ones including background (Thai and Healey, 2002), interference (Du and Chang, 2004), and clutter (Funk et al., 2001). Nevertheless, they can all be considered as variants of the well-known AMD developed by Scharf and Friedlander (1994) and ASD developed by Kraut et al. (2001). Details of such extensions will be discussed in Chapter 12.

Finally, as will be shown in Sections 2.3.2.1 and 12.2.1, ASD is very closely related to the orthogonal subspace projection (OSP).

2.2.3 Subsample Target Detection: Constrained Energy Minimization (CEM)

The ASD presented in Section 2.2.2.2 is derived from subspace projection using maximization of SCR as a criterion for optimality. This section develops a rather different approach, called the constrained energy minimization (CEM) developed in Harsanyi's dissertation (1993) and discussed in great detail in Chang (2003a). It does not assume a signal model or noise/background knowledge. The only knowledge that CEM requires is the subsample target information specified by t as the same level of knowledge required by ASD presented in Section 2.2.2.2. Because there is no signal model involved, CEM does not format a detection problem as a binary composite hypothesis testing. So, CEM is not an LRT-based approach such as AMD and ASD. Moreover, CEM does not need to know background information. As a result, no secondary data are required to produce the background data. Therefore, from a practical point of view, CEM is more realistic and general due to the fact that it requires the least amount of information about subsample target of interest without making assumptions on signal model and noise/background statistics.

The CEM owes its idea to the linearly constrained minimum variance (LCMV) originally proposed by Frost (1972) arising in adaptive beamforming. Suppose that a hyperspectral image is represented by a collection of image pixel vectors, denoted by where for is an L-dimensional pixel vector, N is the total number of pixels in the image, and L is the total number of spectral channels. Further assume that is specified by the target signal of interest to be used for detection. The goal is to find a target detector detecting data samples that contain the desired target signal specified by signature t. Instead of directly appealing for an LRT-based detector, AMD, or a subspace projection-based detector, ASD, an LCMV-based adaptive beamforming approach is used for this purpose. It assumes that the signals arriving at an array from the desired direction will be passed through an adaptive beamformer, while the energies of signals coming from other directions will be minimized at the output of the beamformer. Now, if we interpret the desired direction as the desired signature that specifies targets to be detected and the beamformer's output as a soft decision-maker for target detection, a soft target detector can actually be deigned by a finite impulse response (FIR) linear filter with L filter coefficients , denoted by an L-dimensional vector that minimizes the filter output energy subject to the constraint . More specifically, let yⁱ denote the output of the designed FIR filter resulting from the input rⁱ. Then yⁱ can be expressed by

(2.29)

and the average energy of the filter output is given by

(2.30)

where is the sample auto-correlation matrix of the image. The CEM is developed to solve the following linearly constrained optimization problem

(2.31)

The optimal solution to (2.31) can be derived in Harsanyi (1993) and Chang (2002) by

(2.32)

With the optimal weight w^CEM specified by (2.32), a filter called CEM, denoted by δ^CEM(r), was derived in Harsanyi (1993) and given by

(2.33)

which is also a matched filter and turns out to be ASD in (2.28) with the covariance matrix K replaced by the correlation matrix R. Therefore, except for the sample covariance matrix used in ASD and the sample correlation matrix implemented in CEM, both ASD and CEM are essentially identical to each other in terms of detector structure regardless of the fact that the design rationales for ASD and CEM are quite different.

By further comparing (2.33) to (2.19), the only difference between (2.33) and (2.19) is that the covariance matrix K and used in (2.19) can be simply replaced with R and t in (2.33), respectively. This implies that two different approaches, LRT and LCMV, arrive at the same form of a detector with the same matching signal specified by t. As a consequence, they both give rise to similar performance. This is the major reason why AMD can perform well even if it is derived from Gaussian noise statistics.