2.8 Normal Subgroups
1. a. H = {1, a6, b, ba6} is a subgroup because
![]()
It is not normal in D4 because Ha = {a, a7, ba, ba7} while aH = {a, a7, ba11, ba5}.
c. This is closed because a2b = ba10, a4b = ba8, a6b = ba6; (bak)2 = 1 for each k. Hence H is a subgroup. It is normal, being of index 2.
3. A4 has no subgroup of order 6 [Exercise 34 §2.6] so the only subgroups (normal or not) have order 1, 2, 3 or 4. If 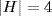 , it contains no 3-cycle and so equals K. Thus K A4 being unique of its order. If
, it contains no 3-cycle and so equals K. Thus K A4 being unique of its order. If  , let H =
, let H = (1, 2, 3)
(1, 2, 3)  without loss of generality. But (1 4)−1(1 2 3)(1 4) = (2 3 4) shows H is not normal. Finally
without loss of generality. But (1 4)−1(1 2 3)(1 4) = (2 3 4) shows H is not normal. Finally 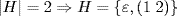 without loss of generality. But (1 3)−1(1 2)(1 3) = (2 3) shows H is not normal.
without loss of generality. But (1 3)−1(1 2)(1 3) = (2 3) shows H is not normal.
5. First aKa−1 is a subgroup, by Theorem 5 §2.3, and aKa−1 ⊆ aHa−1 ⊆ H because H G. If h  H, we must show h(aKa−1)h−1 ⊆ aKa−1. We have h−1Kh = K because K H, so
H, we must show h(aKa−1)h−1 ⊆ aKa−1. We have h−1Kh = K because K H, so
![]()
because K G.
7. Let H = {1, h}. Given g  G, we have g−1hg
G, we have g−1hg  H because H G. But g−1hg ≠ 1 because h ≠ 1, so g−1hg = h. Thus hg = gh for all g
H because H G. But g−1hg ≠ 1 because h ≠ 1, so g−1hg = h. Thus hg = gh for all g  G; that is h
G; that is h  Z(G). If H = {1, a, a2} ⊆ D3 = {1, a, a2, b, ba, ba2} then H D3 but Z(D3) = {1}.
Z(G). If H = {1, a, a2} ⊆ D3 = {1, a, a2, b, ba, ba2} then H D3 but Z(D3) = {1}.
9. (1, 1)  D, (g, g)−1 = (g−1, g−1)
D, (g, g)−1 = (g−1, g−1)  D; (g, g)(g1, g1) = (gg1, gg1)
D; (g, g)(g1, g1) = (gg1, gg1)  D. So D is always a subgroup of G × G. If G is abelian, then G × G is abelian so every subgroup is normal. Conversely, if D is normal, let g, a
D. So D is always a subgroup of G × G. If G is abelian, then G × G is abelian so every subgroup is normal. Conversely, if D is normal, let g, a  G. Then (a, g)−1(g, g)(a, g)
G. Then (a, g)−1(g, g)(a, g)  D, that is (a−1ga, g)
D, that is (a−1ga, g)  D. This means a−1ga = g, so ga = ag. Hence G is abelian.
D. This means a−1ga = g, so ga = ag. Hence G is abelian.
11. Let H and K be subgroups of G with 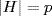 and
and 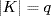 . Then H ∩ K = {1} by Lagrange's theorem. Moreover H G because it is unique of its order, and similarly K G. Hence G ≅ H × K by Corollary 2 of Theorem 6. Since p and q are primes, H and K are cyclic of relatively prime orders. Hence H × K is cyclic by Exercise 25 §2.4.
. Then H ∩ K = {1} by Lagrange's theorem. Moreover H G because it is unique of its order, and similarly K G. Hence G ≅ H × K by Corollary 2 of Theorem 6. Since p and q are primes, H and K are cyclic of relatively prime orders. Hence H × K is cyclic by Exercise 25 §2.4.
13. a. Let g  G, h
G, h  H. Write
H. Write 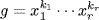 , xi
, xi  X,
X, 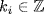 . Then
. Then
![]()
so it suffices to show xkhx−k  H for all x
H for all x  X,
X, 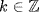 . But then xkhx−k = (xhx−1)k
. But then xkhx−k = (xhx−1)k  H because xhx−1
H because xhx−1  H by hypothesis. The converse is clear.
H by hypothesis. The converse is clear.
15. a. Since a ∉ K, Ka ≠ K, so Ka = GnK (because 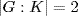 ). Similarly b−1 ∉ K gives Kb−1 = G − K. Thus Ka = Kb−1, so ab
). Similarly b−1 ∉ K gives Kb−1 = G − K. Thus Ka = Kb−1, so ab  K.
K.
17. a. If H = ad
ad  , d
, d  n, let n = md. Since bak is selfinverse for all k, we have
n, let n = md. Since bak is selfinverse for all k, we have
2.
![]()
19. Assume that HK ⊆ KH. If g  KH, say g = kh, then g−1 = h−1k−1
KH, say g = kh, then g−1 = h−1k−1  HK ⊆ KH. If g−1 = k1h1, then
HK ⊆ KH. If g−1 = k1h1, then 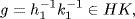 proving that KH ⊆ HK. Hence HK = KH and Lemma 2 applies.
proving that KH ⊆ HK. Hence HK = KH and Lemma 2 applies.
21. 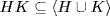 always holds because
always holds because 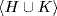 is a subgroup containing H and K. But HK is itself a subgroup (Lemma 2) and contains H and K, so
is a subgroup containing H and K. But HK is itself a subgroup (Lemma 2) and contains H and K, so 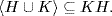
23. a. Let Dn = {1, a, a2, . . ., an−1, b, ba, ba2, . . ., ban−1} where o(a) = n, o(b) = 2 and aba = b. If n = 2m, let H = {1, am}. We have amb = ban−m = bam , so H ⊆ Z(Dn). Thus H Dn. Let K = {1, a2, a4, . . ., an−2, b, ba2, . . ., ban−2}. We have o(a2) = m, o(b) = 2, and a2ba2 = a(aba)a = aba = b. Thus K ≅ Dm. Moreover, K Dn because it is of index 2. But then we have G ≅ H × K ≅ C2 × Dm by Corollary 2 of Theorem 6 since
![]()
24.
a. If H is characteristic in G then aHa−1 = σa(H) ⊆ H where σa is the inner automorphism.
c. Let G = a
a  ×
×  a
a  where o(a) = 2, and define σ : G → G by σ(x, y) = (y, x). It is easy to verify that σ is an automorphism of G and, if H =
where o(a) = 2, and define σ : G → G by σ(x, y) = (y, x). It is easy to verify that σ is an automorphism of G and, if H =  (a, 1)
(a, 1)  = {(1, 1), (a, 1)}, then H G, but σ(H)
= {(1, 1), (a, 1)}, then H G, but σ(H) 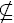 H, so H is not characteristic in G.
H, so H is not characteristic in G.
3. If a  G, let σa : G → G denote the inner automorphism. Then σa(K) = K because K G, so σa : K → K is an automorphism of K. Hence σa(H) = H because H is characteristic in K, that is aHa−1 = H.
G, let σa : G → G denote the inner automorphism. Then σa(K) = K because K G, so σa : K → K is an automorphism of K. Hence σa(H) = H because H is characteristic in K, that is aHa−1 = H.
g. If G = a
a  and H =
and H = am
am  , let σ
, let σ  aut G and let σ(a) = an. If h = amk
aut G and let σ(a) = an. If h = amk  H, then σ(h) = [σ(a)]mk = anmk = (ank)m
H, then σ(h) = [σ(a)]mk = anmk = (ank)m  H. Thus σ(H) ⊆ H. If G is finite it is easier: σ(H) is a subgroup of G of the same order as H so (Theorem 7 §2.4) σ(H) = H. It fails if G is abelian by (c).
H. Thus σ(H) ⊆ H. If G is finite it is easier: σ(H) is a subgroup of G of the same order as H so (Theorem 7 §2.4) σ(H) = H. It fails if G is abelian by (c).
i. Clearly K ⊆ 1G(H) = H. If τ  aut G, then K ⊆ τ−1σ(H) for all σ
aut G, then K ⊆ τ−1σ(H) for all σ  aut G by the definition of K, so τ(K) ⊆ σ(H) for all σ. Thus τ(K) ⊆ K. Similarly, τ−1(K) ⊆ K, so K ⊆ τ(K). Thus K = τ(K) and K is characteristic. Finally, let C ⊆ H, C a characteristic subgroup of G. If σ
aut G by the definition of K, so τ(K) ⊆ σ(H) for all σ. Thus τ(K) ⊆ K. Similarly, τ−1(K) ⊆ K, so K ⊆ τ(K). Thus K = τ(K) and K is characteristic. Finally, let C ⊆ H, C a characteristic subgroup of G. If σ  aut G, then C = σ(C) ⊆ σ(H), so C ⊆ K by the definition of K.
aut G, then C = σ(C) ⊆ σ(H), so C ⊆ K by the definition of K.
25.
a. We have 1  N(X) because 1X1−1 = X. If a, b
N(X) because 1X1−1 = X. If a, b  N(X), then we have aXa−1 = X = bXb−1. Thus a−1
N(X), then we have aXa−1 = X = bXb−1. Thus a−1  N(X) because
N(X) because
![]()
and ab  N(X) because (ab)X(ab)−1 = a[bXb−1]a−1 = a[X]a−1 = X. Hence N(X) is a subgroup of G.
N(X) because (ab)X(ab)−1 = a[bXb−1]a−1 = a[X]a−1 = X. Hence N(X) is a subgroup of G.
c. Suppose K is a subgroup of G and H K. If k  K, then k−1Hk = H by Theorem 3, so k
K, then k−1Hk = H by Theorem 3, so k  N(H). Thus K ⊆ N(H).
N(H). Thus K ⊆ N(H).
26.
a. Write K = core H = ∩ aaHa−1. Clearly 1  K. If g, g1
K. If g, g1  K, then gg1
K, then gg1  aHa−1 for all a, so gg1
aHa−1 for all a, so gg1  K. Also, g−1
K. Also, g−1  a−1H(a−1)−1 for all a, so g
a−1H(a−1)−1 for all a, so g  aHa−1 and g
aHa−1 and g  K. Hence K is a subgroup. If g
K. Hence K is a subgroup. If g  G and k
G and k  K then gkg−1
K then gkg−1  g[(g−1a)H(g−1a)−1]g−1 = aHa−1 for all a, as required.
g[(g−1a)H(g−1a)−1]g−1 = aHa−1 for all a, as required.
c. core H ∩ K ⊆ H ∩ K ⊆ H and core H ∩ K G gives
![]()
Similarly, core (H ∩ K) ⊆ core K, so core (H ∩ K) ⊆ core H ∩ core K. On the other hand, core H ⊆ H and core K ⊆ K gives core H ∩ core K ⊆ core H ∩ K. Since core H ∩ core K G, this gives core H ∩ core K ⊆ core (H ∩ K).
27.
a. First,  is a subgroup of G. If
is a subgroup of G. If 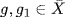 and X ⊆ N G, then 1
and X ⊆ N G, then 1  H and the fact that g, g1
H and the fact that g, g1  N implies that g−1
N implies that g−1  N and gg1
N and gg1  N. Thus
N. Thus 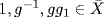 , so
, so 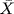 is a subgroup. But if a
is a subgroup. But if a  G and
G and 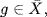 then we have aga−1
then we have aga−1  aNa−1 = N for all N G, X ⊆ N, so
aNa−1 = N for all N G, X ⊆ N, so 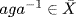 . Thus
. Thus 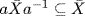 for all a
for all a  G, so
G, so 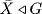 . Clearly
. Clearly  .
.
c. 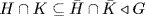 so
so 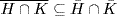 . If G = S3, H = {ε, σ, σ2} and K = {ε, τ}, then
. If G = S3, H = {ε, σ, σ2} and K = {ε, τ}, then 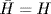 ,
,  , so
, so  .
.
28. a. If c, c1  C(X), then (cc1)x = c(c1x) = c(xc1) = (cx)c1 = xcc1, for all x
C(X), then (cc1)x = c(c1x) = c(xc1) = (cx)c1 = xcc1, for all x  X, so cc1
X, so cc1  C(X). Since cx = xc for all x
C(X). Since cx = xc for all x  X, it follows that xc−1 = c−1x; that is c−1
X, it follows that xc−1 = c−1x; that is c−1  C(X). Finally, 1
C(X). Finally, 1  C(X) is clear.
C(X) is clear.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
