2.9 Factor Groups
1.
a. D6 = {1, a, a2, a3, a4, a5, b, ba, ba2, ba3, ba4, ba5}; K = Z(D6) = {1, a3} by Exercise 26 §2.6. The cosets are
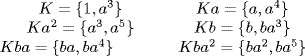
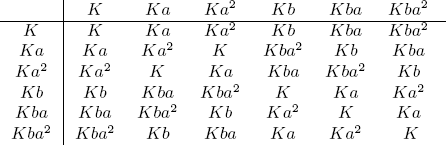
We have 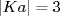 ,
, 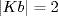 and KaKbKa = Kaba = Kb. Hence D6/K ≅ D3.
and KaKbKa = Kaba = Kb. Hence D6/K ≅ D3.
c. G = A × B, K = {(a, 1)  a
a  A}. Note K G because (x, y)−1(a, 1)(x, y) = (x−1ax, 1)
A}. Note K G because (x, y)−1(a, 1)(x, y) = (x−1ax, 1)  K. If b
K. If b  B, a
B, a  A, note that (ab)(1, b)−1
A, note that (ab)(1, b)−1  K, so
K, so
![]()
Thus G/K = {K(1, b)  b
b  B}. Observe that K(1, b)K(1, b′) = K(1, bb′) gives the Cayley table. Define θ : B → G/K by θ(b) = K(1, b). Then θ is onto, and it is 1 : 1 because θ(b) = θ(b1) gives K(1, b) = K(1, b1), so
B}. Observe that K(1, b)K(1, b′) = K(1, bb′) gives the Cayley table. Define θ : B → G/K by θ(b) = K(1, b). Then θ is onto, and it is 1 : 1 because θ(b) = θ(b1) gives K(1, b) = K(1, b1), so 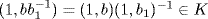 . Hence
. Hence 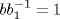 , b = b1. Finally, θ(b) · θ(b1) = K(1, b)K(1, b1) = K(1, bb1) = θ(bb1). So θ is an isomorphism; G/K ≅ B.
, b = b1. Finally, θ(b) · θ(b1) = K(1, b)K(1, b1) = K(1, bb1) = θ(bb1). So θ is an isomorphism; G/K ≅ B.
3. a. We have G = a
a  , so G/K =
, so G/K = Ka
Ka  . We claim
. We claim 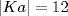 . Certainly (Ka)12 = Ka12 = K. But
. Certainly (Ka)12 = Ka12 = K. But 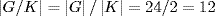 , so,
, so, 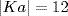 because Ka generates G/K. Now
because Ka generates G/K. Now 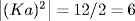 by Theorem 7 §2.4. Similarly,
by Theorem 7 §2.4. Similarly, 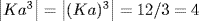 , and
, and 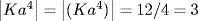 . Finally, Ka5 = (Ka)5 is a generator of G/K because gcd (5, 12) = 1 (Theorem 6 §2.4). Thus
. Finally, Ka5 = (Ka)5 is a generator of G/K because gcd (5, 12) = 1 (Theorem 6 §2.4). Thus 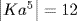 .
.
4. a. G = a
a  ×
×  b
b  with o(a) = 8 and o(b) = 12, and K =
with o(a) = 8 and o(b) = 12, and K = (a2, b3)
(a2, b3)  . We want
. We want 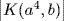 in G/K. Then, as (a4, b)12 = (1, 1)
in G/K. Then, as (a4, b)12 = (1, 1)  K,
K, 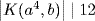 , so
, so 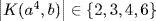 . But since none of
. But since none of
![]()
or (a4, b)6 = (1, b6) are in K, 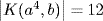 .
.
5. a. We have Ka2 = K because a2  K. So o(Ka2) = 1. Next we have (Ka3)2 = Ka6 = K, so o(Ka3) divides 2. Since
K. So o(Ka2) = 1. Next we have (Ka3)2 = Ka6 = K, so o(Ka3) divides 2. Since
![]()
Similarly (Kba)2 = K(ba)2 = K and ba ∉ K, so o(Kba) = 2. Finally (Ka5)2 = Ka10 = K, so o(Ka5) = 2 because a5 ∉ K.
7. If 0 < n < m in 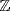 , then
, then 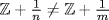 because
because 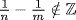 . Hence
. Hence 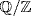 contains the infinite set
contains the infinite set 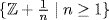 . Now let
. Now let 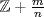 be any element of
be any element of 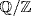 . Then
. Then 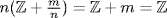 , so
, so 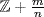 has finite order.
has finite order.
9. If o(g) = n, then gn = 1, so (Kg)n = Kgn = K1 = K. Thus o(Kg) divides n.
11. Let o(g) = n, g  G. Then (Kg)n = Kgn = K in G/K. On the other hand,
G. Then (Kg)n = Kgn = K in G/K. On the other hand, 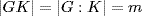 , so (Kg)m = K by Lagrange's theorem. But gcd (m, n) = 1 implies 1 = nx + my,
, so (Kg)m = K by Lagrange's theorem. But gcd (m, n) = 1 implies 1 = nx + my, 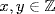 , so
, so
![]()
Thus g  K.
K.
13.
a. If z  Z(G), then zK
Z(G), then zK  Z(G/K), so z
Z(G/K), so z  K. Then z
K. Then z  Z(K), so z = 1.
Z(K), so z = 1.
c. If g  G, then
G, then 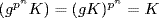 for some n, so
for some n, so 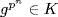 . Thus
. Thus 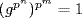 , so
, so 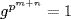 , so o(g) = pk for some k ≤ n + m.
, so o(g) = pk for some k ≤ n + m.
15. If Kg  G/K, then g
G/K, then g
 X
X  , say
, say 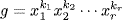 , xi
, xi  X,
X, 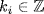 . Then Kg = (Kx1)k1(Kx2)k2
. Then Kg = (Kx1)k1(Kx2)k2 (Kxr)kr
(Kxr)kr 
 {Kx
{Kx  x
x  X}
X}  .
.
17.
a. If o(g) = n, o(g1) = m, then 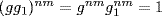 because G is abelian, and (g−1)n = 1.
because G is abelian, and (g−1)n = 1.
c. If G is torsion, it is clear that H and G/H are torsion. Conversely, if g  G then (Hg)n = H for some n, so gn
G then (Hg)n = H for some n, so gn  H. Thus (gn)m = 1 for some m ≠ 0, that is g
H. Thus (gn)m = 1 for some m ≠ 0, that is g  T(G). Hence T(G) = G.
T(G). Hence T(G) = G.
19.
a. If G is abelian, then G/{1} is abelian, so G′ ⊆ {1}. Thus G′ = {1}.
c. Write
![]()
Let K =  a2
a2  = {1, a2, a4}. Then a2b = ba4 and a4b = ba2, so b−1Kb ⊆ K. Hence K D6 and D6/K is abelian (it has order 4). This means
= {1, a2, a4}. Then a2b = ba4 and a4b = ba2, so b−1Kb ⊆ K. Hence K D6 and D6/K is abelian (it has order 4). This means 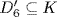 . But
. But 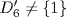 because D6 is not abelian. Thus
because D6 is not abelian. Thus  .
.
21. Given commutators [a, b] in G′ and [x, y] in H′, we have
![]()
If (g, h)  G′ × H′, then (g, h) = (g, 1)(1, h) and each of (g, 1) and (1, h) are products of commutators of the form ([a, b], [x, y]). Hence G′ × H′ ⊆ (G × H)′. Conversely [(a, x), (b, y)] = ([a, x], [b, y]) shows that every commutator of G × H lies in G′ × H′, so (G × H)′ ⊆ G′ × H′.
G′ × H′, then (g, h) = (g, 1)(1, h) and each of (g, 1) and (1, h) are products of commutators of the form ([a, b], [x, y]). Hence G′ × H′ ⊆ (G × H)′. Conversely [(a, x), (b, y)] = ([a, x], [b, y]) shows that every commutator of G × H lies in G′ × H′, so (G × H)′ ⊆ G′ × H′.
23. a. The unity K = K1 of G/K is in H/K because 1  H. If Kh and Kh′ are in H/K where h, h′
H. If Kh and Kh′ are in H/K where h, h′  H, then Kh · Kh′ = Khh′
H, then Kh · Kh′ = Khh′  H/K and also (Kh)−1 = Kh−1
H/K and also (Kh)−1 = Kh−1  H/K. Use the subgroup test.
H/K. Use the subgroup test.
25. a. [Ka, Kb] = (Ka)(Kb)(Ka−1)(Kb−1) = K(aba−1b−1) = K[a, b].
27. Let σ : G → G be an automorphism. We must show σ(H) = H. Define 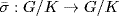 by
by 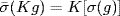 . Since K is characteristic in G,
. Since K is characteristic in G, 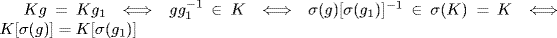 . Hence
. Hence 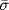 is well-defined and one-to-one; it is onto because σ is onto. Finally,
is well-defined and one-to-one; it is onto because σ is onto. Finally, 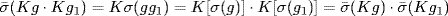 . Hence σ is an automorphism of G/K, so
. Hence σ is an automorphism of G/K, so 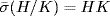 by hypothesis. Hence, if h
by hypothesis. Hence, if h  H,
H, 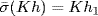 , h1
, h1  H, so
H, so 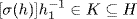 . Thus σ(h)
. Thus σ(h)  H, whence σ(H) ⊆ H. Similarly σ−1(H) ⊆ H and so H ⊆ σ(H). Thus H = σ(H).
H, whence σ(H) ⊆ H. Similarly σ−1(H) ⊆ H and so H ⊆ σ(H). Thus H = σ(H).
1. a. Suppose 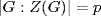 is a prime. Then
is a prime. Then 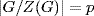 , so the group G/Z(G) is cyclic by Lagrange's theorem (Corollary 3). Then Theorem 2 shows G is abelian. Thus Z(G) = G, so
, so the group G/Z(G) is cyclic by Lagrange's theorem (Corollary 3). Then Theorem 2 shows G is abelian. Thus Z(G) = G, so 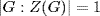 , a contradiction.
, a contradiction.
29. Let n = kd and Dn = {1, a, . . ., an−1, b, ba, . . ., ban−1}, o(a) = n, o(b) = 2, aba = b. Let K = ak
ak  . Then K G because b−1akb = a−k
. Then K G because b−1akb = a−k  K. In Dn/K, let
K. In Dn/K, let 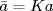 ,
, 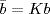 . Then
. Then 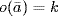 ,
, 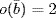 and
and
![]()
Since 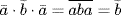 , Dn/K ≅ Dk.
, Dn/K ≅ Dk.
31. Let A ⊆ C4 and B ⊆ C ⊆ C8where |A| = |B| = 2 and |C| = 4 . (a) Let K = A × C and H = C4 × B. Then K ≅ C2 × C4 ≅ H, but 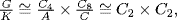 while
while 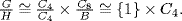 So
So 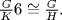
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
