3.5 Ordered Integral Domains
1.
a. (b + c) − (a + c) = b − a 
R+.
R+.
c. (− a) − (− b) = b − a R+.
R+.
e. Since a < b and c > 0, ac < bc by Lemma 1. Similarly bc < bd because b > 0, again by Lemma 1. Finally then ac < bd by Lemma 1.
2.
a. a ≤ a because a = a.
c. Let a ≤ b and b ≤ c. If a = b then b ≤ c is a ≤ c; if b = c then a ≤ b is a ≤ c. Otherwise a < b and b < c so a < c by Lemma 1.
3.
a. If a ≥ 0 then |a| = a ≥ 0. If a < 0 then −a = 0 − a R+ so |a| = − a > 0.
R+ so |a| = − a > 0.
c. If either a = 0 or b = 0 then |ab| = 0 = |a||b|.
If a > 0, b > 0, then ab > 0 so |ab| = ab = |a||b|.
If a > 0, b < 0, then ab < 0 so |ab| = − ab = a(− b) = |a||b|.
If a < 0, b > 0, as above.
If a < 0, b < 0 then ab > 0 so |ab| = ab = (− a)(− b) = |a||b|.
4. If a is such that b ≤ a for all b then a + 1 ≤ a, whence 1 ≤ 0, a contradiction.
5.
a.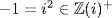 
and 
would be a contradiction.
and 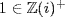would be a contradiction.
7. 
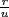and 
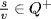, so ru R+ and sv R+. Thus (using Lemma 1(5)):
and , so ru R+ and sv R+. Thus (using Lemma 1(5)):
Hence Q+ satisfies P1. Now let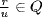 
. Then exactly one of ru = 0, ru R+ and −(ru) R+ is true. But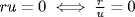 
(because u ≠ 0); 
; and 
. Thus Q+ satisfies P2.
. Then exactly one of ru = 0, ru R+ and −(ru) R+ is true. But (because u ≠ 0); ; and 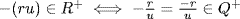. Thus Q+ satisfies P2.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.