6.3 Splitting Fields
1.
a. x3 + 1 = (x + 1)(x2 − x + 1), and the roots of x2 − x + 1 are 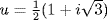 and
and  so
so 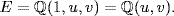 But
But 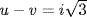 so it follows that
so it follows that 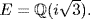 Since
Since 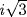 is a root of the polynomial x2 + 3, and since x3 + 3 is irreducible over
is a root of the polynomial x2 + 3, and since x3 + 3 is irreducible over  (no root), then it is the minimal polynomial of
(no root), then it is the minimal polynomial of 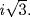 Hence
Hence 
c. f = (x2 − 7)(x2 + 1) so 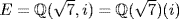 . Thus,
. Thus,
![]()
Moreover, 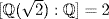 because x2 − 2 is irreducible over
because x2 − 2 is irreducible over  and
and 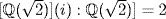 because x2 + 1 has no root in
because x2 + 1 has no root in 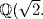 Hence
Hence  by the multiplication theorem.
by the multiplication theorem.
2.
a. f = (x2 − 2x − 2)(x2 − 5) so the roots are 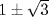 and
and 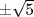 . Hence
. Hence 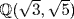 is the splitting field.
is the splitting field.
4.
a. f = (x + 1)(x2 + x + 1) and x2 + x + 1 is irreducible over 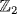 . If u is a root then the other is given by
. If u is a root then the other is given by 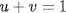 ;
; 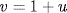 . Thus
. Thus 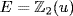 and f = (x + 1)(x + u)(x + 1 + u).
and f = (x + 1)(x + u)(x + 1 + u).
c. f is irreducible over 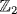 . If u is a root then, by long division, f = (x + u)g where g = x2 + (1 + u)x + (u + u2). We claim that g also splits in
. If u is a root then, by long division, f = (x + u)g where g = x2 + (1 + u)x + (u + u2). We claim that g also splits in 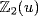 , so
, so 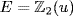 . We try possibilities to get g(u2) = 0. Then the other root
. We try possibilities to get g(u2) = 0. Then the other root  satisfies
satisfies 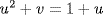 , so
, so 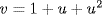 . Thus
. Thus
![]()
e. f = (x2 − 2)(x2 + 1) = (x2 + 1)2 over 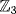 . Now x2 + 1 is irreducible over
. Now x2 + 1 is irreducible over 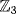 (no root in
(no root in 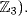 If u is a root then x2 + 1 = x2 − u2 = (x − u)(x + u). Thus
If u is a root then x2 + 1 = x2 − u2 = (x − u)(x + u). Thus 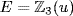 and f = (x − u)2(x + u)2.
and f = (x − u)2(x + u)2.
5. The roots are 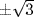 and
and 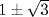 . So
. So 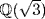 is the splitting field for both.
is the splitting field for both.
6.
a. If 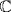 were the splitting field of
were the splitting field of  then
then 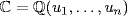 . Thus
. Thus  would be algebraic, contradicting the fact that π or e is transcendental.
would be algebraic, contradicting the fact that π or e is transcendental.
7. We have f = a(x − u1)  (x − um) in E[x]. If p is a monic, irreducible factor of g in E[x] then p|f so p = x − ui for some i. Thus
(x − um) in E[x]. If p is a monic, irreducible factor of g in E[x] then p|f so p = x − ui for some i. Thus
![]()
by the unique factorization theorem, as required.
9. If gcd (f, g) = 1 let 1 = fh + gk; h, k in F[x]. If E ⊇ F is an extension containing an element u such that f(u) = 0 = g(u), substitution gives
![]()
a contradiction. Conversely, let d = gcd (f, g). If d ≠ 1 then deg d ≥ 1 so let E ⊇ F be a field containing a root u of d. Then d|f and d|g means f(u) = 0 = g(u), contrary to hypothesis.
11. We have E = F(u1, . . ., un) where f = a(x − u1)  (x − un), a
(x − un), a  F, ui
F, ui  E. Since L ⊇ F, E = L(u1, . . ., un), and a
E. Since L ⊇ F, E = L(u1, . . ., un), and a  L, ui
L, ui  E, show f splits in E over L.
E, show f splits in E over L.
13. The roots of xp − 1 are 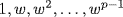 (Theorem 6, Appendix A) so
(Theorem 6, Appendix A) so 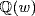 is the splitting field. We have xp − 1 = (x − 1)Φp where
is the splitting field. We have xp − 1 = (x − 1)Φp where
![]()
is the pth cyclotomic polynomial. Then Φp is irreducible over 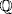 by Example 13 §4.2, and so is the minimal polynomial of
by Example 13 §4.2, and so is the minimal polynomial of  (
( is a root of Φp). Hence
is a root of Φp). Hence  by Theorem 4 §6.2.
by Theorem 4 §6.2.
15. Let K ⊇ E be a field in which f has a root  . Write deg f = m and g = n so that [F(u) : F] = n and
. Write deg f = m and g = n so that [F(u) : F] = n and 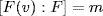 are relatively prime. By Exercise 21 §6.2,
are relatively prime. By Exercise 21 §6.2, 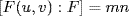 . Now let p be the minimal polynomial of
. Now let p be the minimal polynomial of  over F(u); we show f = p. We have
over F(u); we show f = p. We have 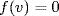 so p|f in F(u)[x], and so it is enough to show that deg p = m. We have
so p|f in F(u)[x], and so it is enough to show that deg p = m. We have  deg p, so
deg p, so
![]()
by the multiplication theorem. Thus p = m as required.
17. The map f → fσ is clearly onto (since σ is onto). If 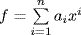 then
then
![]()
so fσ = 0 implies σ(ai) = 0 for all i, which in turn implies ai = 0 for all i, whence f = 0. Thus fσ is one-to-one if we can show it is a ring homomorphism. If 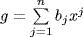 ,
,
![]()
Similarly
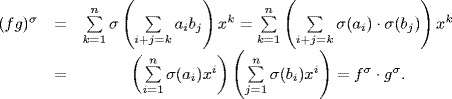
Hence the map is a ring isomorphism (clearly 1σ = 1). Finally, if a  F let g = a be the constant polynomial. Then g
F let g = a be the constant polynomial. Then g  gσ means a
gσ means a  σ(a). So the map extends σ.
σ(a). So the map extends σ.
19. If π were algebraic over  then π would satisfy a nonzero polynomial f in
then π would satisfy a nonzero polynomial f in  . But f splits in
. But f splits in  because
because  is algebraically closed, so this would imply that
is algebraically closed, so this would imply that 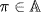 , a contradiction.
, a contradiction.
20.
a. We show 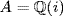 . Clearly
. Clearly 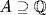 is algebraic. We must show that if u
is algebraic. We must show that if u  E is algebraic over
E is algebraic over 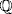 then u
then u  A. Since u is algebraic over A, we show that u
A. Since u is algebraic over A, we show that u  A implies u is transcendental over A. We have E = A(π) so this follows from Exercise 31 §6.2 if we can show that π is transcendental over A. But if π were algebraic over A it would be algebraic over
A implies u is transcendental over A. We have E = A(π) so this follows from Exercise 31 §6.2 if we can show that π is transcendental over A. But if π were algebraic over A it would be algebraic over 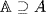 , contrary to the preceding exercise.
, contrary to the preceding exercise.
21. (1) ⇒ (2). If E ⊇ F is the splitting field of f  F[x], then E = F(u1, . . ., um) where the ui are the roots of f in E, so [E : F] is finite by Theorem 6 §6.2. If p F[x] is irreducible with a root u
F[x], then E = F(u1, . . ., um) where the ui are the roots of f in E, so [E : F] is finite by Theorem 6 §6.2. If p F[x] is irreducible with a root u  E, let
E, let  be a root in some field K ⊇ E. Then p is the minimal polynomial of both u and
be a root in some field K ⊇ E. Then p is the minimal polynomial of both u and  so let
so let 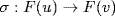 be an isomorphism (Theorem 4 §6.2). Now E is a splitting field of f over F(u), and
be an isomorphism (Theorem 4 §6.2). Now E is a splitting field of f over F(u), and 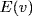 is a splitting field of f over
is a splitting field of f over 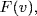 so Theorem 3 shows
so Theorem 3 shows 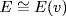 via an isomorphism extending σ. Hence
via an isomorphism extending σ. Hence 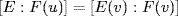 , so
, so
![]()
Since E is an F-subspace of 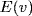 , this shows
, this shows 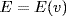 , and so
, and so 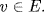 (2) ⇒ (1). Since E ⊇ F is finite, let E = F(u1, . . ., un). Each ui is algebraic over F, say with minimal polynomial pi
(2) ⇒ (1). Since E ⊇ F is finite, let E = F(u1, . . ., un). Each ui is algebraic over F, say with minimal polynomial pi  F[x]. Since pi splits in E by (2), E is the splitting field of f = p1p2
F[x]. Since pi splits in E by (2), E is the splitting field of f = p1p2  pn.
pn.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
