6.4 Finite Fields
1.
(a) In 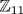 , 22 = 4, 23 = 8, 24 = 5, 25 = − 1, so o(2) = 10. Thus 2 is a primitive element.
, 22 = 4, 23 = 8, 24 = 5, 25 = − 1, so o(2) = 10. Thus 2 is a primitive element.
(c) 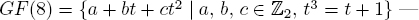 since x3 + x + 1 is irreducible in
since x3 + x + 1 is irreducible in  . In this case GF(8)∗ has order 7, so every nonzero element except 1 is primitive by Lagrange's theorem.
. In this case GF(8)∗ has order 7, so every nonzero element except 1 is primitive by Lagrange's theorem.
3. Both p and q have no root in 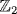 , so they are irreducible. Hence both rings are fields of order 23 and so are isomorphic by Theorem 4.
, so they are irreducible. Hence both rings are fields of order 23 and so are isomorphic by Theorem 4.
4. (a) 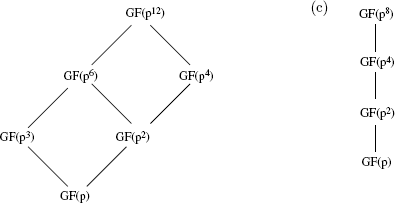

5. First x4 + x + 1 is irreducible over  (it has no root, x2 + x + 1 is the only irreducible quadratic, and (x2 + x + 1)2 = x4 + x2 + 1). Hence
(it has no root, x2 + x + 1 is the only irreducible quadratic, and (x2 + x + 1)2 = x4 + x2 + 1). Hence
![]()
Now t3 ≠ 1 and t5 = t(t + 1) = t + t2 ≠ 1, so o(t) = 15. Thus t is primitive. Since 16 = 24 the subfields of GF(24) are GF(2), GF(22) and GF(24). Clearly  and GF(24) = GF(16). Finally o(t5) = 3 so by the discussion following Corollary 2 of Theorem 7,
and GF(24) = GF(16). Finally o(t5) = 3 so by the discussion following Corollary 2 of Theorem 7,
![]()
7. E is finite so 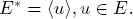 Thus
Thus  , whence E = F(u).
, whence E = F(u).
9. If  and |G| = n, then
and |G| = n, then 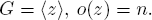 . Thus G = Un —the group of all nth roots of unity.
. Thus G = Un —the group of all nth roots of unity.
11. The Frobenius automorphism σ : F → F is given by σ(b) = bp. This is onto, so each a  F has the form a = σ(b) = bp for some b
F has the form a = σ(b) = bp for some b  F.
F.
13. Write f = a0 + a1x +  + anxn,
+ anxn, 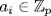 . If σ : E → E is the Frobenius map defined by σ(t) = tp, then σ(a) = a for all
. If σ : E → E is the Frobenius map defined by σ(t) = tp, then σ(a) = a for all 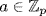 by Fermat's theorem. Since 0 = f(u) = a0 + a1u +
by Fermat's theorem. Since 0 = f(u) = a0 + a1u +  + anun, we obtain
+ anun, we obtain
![]()
15. If u GF(2n) is a root of x2 + x + 1 then u2 = u + 1. Hence 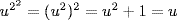 . Then
. Then
![]()
In general 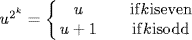 . But
. But 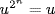 here because |GF(2n)| = 2n, so we have a contradiction because n is odd.
here because |GF(2n)| = 2n, so we have a contradiction because n is odd.
17. Let d = gcd (f, f′) and write d = fg + f′h where g and h are in F[x]. If d = 1, suppose f has a repeated root a in E ⊇ F. Then x − a divides both f and f′ in E[x], and so divides d = 1, a contradiction. Conversely, if d ≠ 1, let E be a splitting field of f over F. Then d|f implies d has a root a in E, so x − a divides f and f′, a contradiction by Theorem 3.
18.
a. Let f have no repeated root in a splitting field E ⊇ F, and suppose that f′ = 0 . If f(a) = 0, a  E, then f′ = 0 implies (x − a) divides f′, so a is a repeated root by Theorem 3. Conversely, if f′ ≠ 0 let d = gcd (f, f′). Then d|f so d = 1 or d = because f is irreducible. But d = f is impossible because f does not divide f′. So d = 1, say 1 = fg + f′h with g, h
E, then f′ = 0 implies (x − a) divides f′, so a is a repeated root by Theorem 3. Conversely, if f′ ≠ 0 let d = gcd (f, f′). Then d|f so d = 1 or d = because f is irreducible. But d = f is impossible because f does not divide f′. So d = 1, say 1 = fg + f′h with g, h  F[x]. Now let a be a repeated root of f in a field E ⊇ F. Then x − a divides f and f′ by Theorem 3, so x − a divides 1 in E[x], a contradiction.
F[x]. Now let a be a repeated root of f in a field E ⊇ F. Then x − a divides f and f′ by Theorem 3, so x − a divides 1 in E[x], a contradiction.
19. Use Exercise 18(a). If 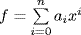 then
then 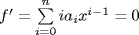 means iai = 0 for i ≥ 1. Thus ai = 0 if p does not divide i, so
means iai = 0 for i ≥ 1. Thus ai = 0 if p does not divide i, so
![]()
where g = a0+ apx + a2px2 +  . Conversely, if f = g(xp), Theorem 2 gives f′ = g′(xp) · pxp−1 = 0.
. Conversely, if f = g(xp), Theorem 2 gives f′ = g′(xp) · pxp−1 = 0.
21. Let 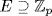 be a splitting field of f. Suppose that u
be a splitting field of f. Suppose that u  E satisfies f(u) = 0. If
E satisfies f(u) = 0. If 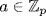 , then
, then
![]()
Thus  consists of p distinct roots of f, and so is the set of all roots of f (since °f = p) . Since E is generated over
consists of p distinct roots of f, and so is the set of all roots of f (since °f = p) . Since E is generated over  by these roots, we have
by these roots, we have 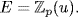
22. Write 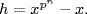
a. Let 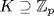 be a field containing a root u of f. Since f is irreducible, it is the minimal polynomial of u over
be a field containing a root u of f. Since f is irreducible, it is the minimal polynomial of u over 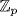 . If we write
. If we write 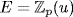 then
then 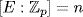 and so |E| = pn. Then u is a root of h so f|h in E[x], say h = qf. But h = q0f + r in
and so |E| = pn. Then u is a root of h so f|h in E[x], say h = qf. But h = q0f + r in  by the division algorithm, so this holds in E[x]. By the uniqueness in E[x], we get
by the division algorithm, so this holds in E[x]. By the uniqueness in E[x], we get 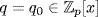 and
and 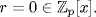
c. Here  , so the irreducible divisors are of degree 1 or 3 by (b). Then
, so the irreducible divisors are of degree 1 or 3 by (b). Then
![]()
23. If char F = 2 then |F| = 2n so  for all a. Thus
for all a. Thus 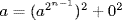 . So assume char F = p ≠ 2. Write X = {u2 |u
. So assume char F = p ≠ 2. Write X = {u2 |u  F}. If F = {0, u1, − u1, u2, − u2, . . . } then
F}. If F = {0, u1, − u1, u2, − u2, . . . } then 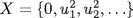 . If we write |F| = q, then
. If we write |F| = q, then  . Now let u
. Now let u  F and write Y = {a − u2 | u F}. Then |X| = |Y| so both sets have more than
F and write Y = {a − u2 | u F}. Then |X| = |Y| so both sets have more than 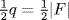 elements. Thus X∩ Y ≠ , say
elements. Thus X∩ Y ≠ , say 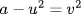 , u,
, u, 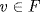 , so
, so 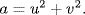
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
