2.2 Positional Notation
How many ones are there in 943? That is, how many actual things does the number 943 represent? Well, in grade school terms, you might say there are 9 hundreds plus 4 tens plus 3 ones. Or, said another way, there are 900 ones plus 40 ones plus 3 ones. So how many ones are there in 754? 700 ones plus 50 ones plus 4 ones. Right? Well, maybe. The answer depends on the base of the number system you are using. This answer is correct in the base-10, or decimal, number system, which is the number system humans use every day. But that answer is not correct in other number systems.
The base of a number system specifies the number of digits used in the system. The digits always begin with 0 and continue through one less than the base. For example, there are 2 digits in base 2: 0 and 1. There are 8 digits in base 8: 0 through 7. There are 10 digits in base 10: 0 through 9. The base also determines what the positions of digits mean. When you add 1 to the last digit in the number system, you have a carry to the digit position to the left.
Numbers are written using positional notation. The rightmost digit represents its value multiplied by the base to the zeroth power. The digit to the left of that one represents its value multiplied by the base to the first power. The next digit represents its value multiplied by the base to the second power. The next digit represents its value multiplied by the base to the third power, and so on. You are so familiar with positional notation that you probably don’t think about it. We used it instinctively to calculate the number of ones in 943.

A more formal way of defining positional notation is to say that the value is represented as a polynomial in the base of the number system. But what is a polynomial? A polynomial is a sum of two or more algebraic terms, each of which consists of a constant multiplied by one or more variables raised to a nonnegative integral power. When defining positional notation, the variable is the base of the number system. Thus 943 is represented as a polynomial as follows, with x acting as the base:
9 * x2 + 4 * x1 + 3 * x0
Let’s express this idea formally. If a number in the base-R number system has n digits, it is represented as follows, where di represents the digit in the ith position in the number:
dn * Rn–1 + dn–1 * Rn–2 + . . . + d2 * R + d1
Look complicated? Let’s look at a concrete example: 63578 in base 10. Here n is 5 (the number has five digits), and R is 10 (the base). The formula says that the fifth digit (last digit on the left) is multiplied by the base to the fourth power; the fourth digit is multiplied by the base to the third power; the third digit is multiplied by the base to the second power; the second digit is multiplied by the base to the first power; and the first digit is not multiplied by anything.
6 * 104 + 3 * 103 + 5 * 102 + 7 * 101 + 8
In the previous calculation, we assumed that the number base is 10. This is a logical assumption because our number system is base 10. However, there is no reason why the number 943 couldn’t represent a value in base 13. If so, to determine the number of ones, we would have to convert it to base 10.
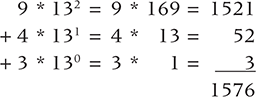
Therefore, 943 in base 13 is equal to 1576 in base 10. Keep in mind that these two numbers have an equivalent value. That is, both represent the same number of things. If one bag contains 943 (base 13) beans and a second bag contains 1576 (base 10) beans, then both bags contain the exact same number of beans. Number systems just allow us to represent values in various ways.
Note that in base 10, the rightmost digit is the “ones” position. In base 13, the rightmost digit is also the “ones” position. In fact, this is true for any base, because anything raised to the power 0 is 1.
Why would anyone want to represent values in base 13? It isn’t done very often, granted, but it is another example that demonstrates how all number systems work. For example, a computing technique called hashing takes numbers and scrambles them, and one way to scramble numbers is to interpret them in a different base.
Other bases, such as base 2 (binary), are particularly important in computer processing. Let’s explore these bases in more detail.
Binary, Octal, and Hexadecimal
The base-2 (binary) number system is particularly important in computing. It is also helpful to be familiar with number systems that are powers of 2, such as base 8 (octal) and base 16 (hexadecimal). Recall that the base value specifies the number of digits in the number system. Base 10 has ten digits (0–9), base 2 has two digits (0–1), and base 8 has eight digits (0–7).
Therefore, the number 943 could not represent a value in any base less than base 10, because the digit 9 doesn’t exist in those bases. It is, however, a valid number in base 10 or any base higher than that. Likewise, the number 2074 is a valid number in base 8 or higher, but it simply does not exist (because it uses the digit 7) in any base lower than that.
What are the digits in bases higher than 10? We need symbols to represent the digits that correspond to the decimal values 10 and beyond. In bases higher than 10, we use letters as digits. We use the letter A to represent the number 10, B to represent 11, C to represent 12, and so forth. Therefore, the 16 digits in base 16 are:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Let’s look at values in octal, hexadecimal, and binary to see what they represent in base 10. For example, let’s calculate the decimal equivalent of 754 in octal (base 8). As before, we just expand the number in its polynomial form and add up the numbers.
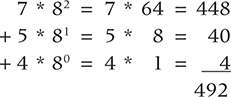
Let’s convert the hexadecimal number ABC to decimal:
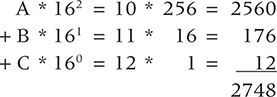
Note that we perform the exact same calculation to convert the number to base 10. We just use a base value of 16 this time, and we have to remember what the letter digits represent. After a little practice you won’t find the use of letters as digits that strange.
Finally, let’s convert a binary (base-2) number 1010110 to decimal. Once again, we perform the same steps—only the base value changes:
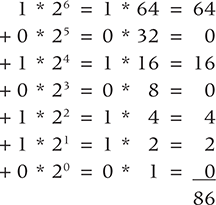
Recall that the digits in any number system go up to one less than the base value. To represent the base value in any base, you need two digits. A 0 in the rightmost position and a 1 in the second position represent the value of the base itself. Thus 10 is ten in base 10, 10 is eight in base 8, and 10 is sixteen in base 16. Think about it. The consistency of number systems is actually quite elegant.
Addition and subtraction of numbers in other bases are performed exactly like they are on decimal numbers.
Arithmetic in Other Bases
Recall the basic idea of arithmetic in decimal: 0 + 1 is 1, 1 + 1 is 2, 2 + 1 is 3, and so on. Things get interesting when you try to add two numbers whose sum is equal to or larger than the base value—for example, 1 + 9. Because there isn’t a symbol for 10, we reuse the same digits and rely on position. The rightmost digit reverts to 0, and there is a carry into the next position to the left. Thus 1 + 9 equals 10 in base 10.
The rules of binary arithmetic are analogous, but we run out of digits much sooner. That is, 0 + 1 is 1, and 1 + 1 is 0 with a carry. Then the same rule is applied to every column in a larger number, and the process continues until we have no more digits to add. The example below adds the binary values 101110 and 11011. The carry value is marked above each column in color.
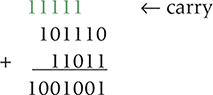
We can convince ourselves that this answer is correct by converting both operands to base 10, adding them, and comparing the result: 101110 is 46, 11011 is 27, and the sum is 73. Of course, 1001001 is 73 in base 10.
The subtraction facts that you learned in grade school were that 9 – 1 is 8, 8 – 1 is 7, and so on, until you try to subtract a larger digit from a smaller one, such as 0 – 1. To accomplish this feat, you have to “borrow one” from the next left digit of the number from which you are subtracting. More precisely, you borrow one power of the base. So, in base 10, when you borrow, you borrow 10. The same logic applies to binary subtraction. Every time you borrow in a binary subtraction, you borrow 2. Here are two examples with the borrowed values marked above.
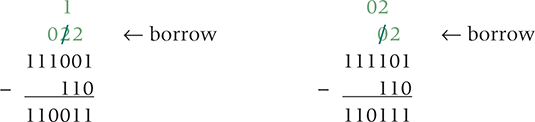
Once again, you can check the calculation by converting all values to base 10 and subtracting to see if the answers correspond.
Power-of-2 Number Systems
Binary and octal numbers share a very special relationship: Given a number in binary, you can read it off in octal; given a number in octal, you can read it off in binary. For example, take the octal number 754. If you replace each digit with the binary representation of that digit, you have 754 in binary. That is, 7 in octal is 111 in binary, 5 in octal is 101 in binary, and 4 in octal is 100 in binary, so 754 in octal is 111101100 in binary.
To facilitate this type of conversion, the table below shows counting in binary from 0 through 10 with their octal and decimal equivalents.
| BINARY | OCTAL | DECIMAL |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 10 | 2 | 2 |
| 11 | 3 | 3 |
| 100 | 4 | 4 |
| 101 | 5 | 5 |
| 110 | 6 | 6 |
| 111 | 7 | 7 |
| 1000 | 10 | 8 |
| 1001 | 11 | 9 |
| 1010 | 12 | 10 |
To convert from binary to octal, you start at the rightmost binary digit and mark the digits in groups of threes. Then you convert each group of three to its octal value.
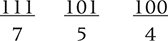
Let’s convert the binary number 1010110 to octal, and then convert that octal value to decimal. The answer should be the equivalent of 1010110 in decimal, or 86.
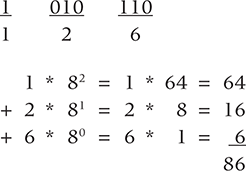
The reason that binary can be immediately converted to octal and octal to binary is that 8 is a power of 2. There is a similar relationship between binary and hexadecimal. Every hexadecimal digit can be represented in four binary digits. Let’s take the binary number 1010110 and convert it to hexadecimal by marking the digits from right to left in groups of four.

Now let’s convert ABC in hexadecimal to binary. It takes four binary digits to represent each hex digit. A in hexadecimal is 10 in decimal and therefore is 1010 in binary. Likewise, B in hexadecimal is 1011 in binary, and C in hexadecimal is 1100 in binary. Therefore, ABC in hexadecimal is 101010111100 in binary.
Rather than confirming that 101010111100 is 2748 in decimal directly, let’s mark it off in octal and convert the octal.
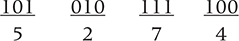
Thus 5274 in octal is 2748 in decimal.
In the next section, we show how to convert base-10 numbers to the equivalent number in another base.
Converting from Base 10 to Other Bases
The rules for converting base-10 numbers involve dividing by the base into which you are converting the number. From this division, you get a quotient and a remainder. The remainder becomes the next digit in the new number (going from right to left), and the quotient replaces the number to be converted. The process continues until the quotient is zero. Let’s write the rules in a different form.
These rules form an algorithm for converting from base 10 to another base. An algorithm is a logical sequence of steps that solves a problem. We have much more to say about algorithms in later chapters. Here we show one way of describing an algorithm and then apply it to perform the conversions.
The first line of the algorithm tells us to repeat the next three lines until the quotient from our division becomes zero. Let’s convert the decimal number 2748 to hexadecimal. As we’ve seen in previous examples, the answer should be ABC.

The remainder (12) is the first digit in the hexadecimal answer, represented by the digit C. So the answer so far is C. Since the quotient is not zero, we divide it (171) by the new base.

The remainder (11) is the next digit to the left in the answer, which is represented by the digit B. Now the answer so far is BC. Since the quotient is not zero, we divide it (10) by the new base.
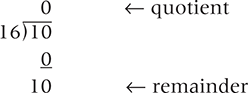
The remainder (10) is the next digit to the left in the answer, which is represented by the digit A. Now the answer is ABC. The quotient is zero, so we are finished, and the final answer is ABC.
Binary Values and Computers
Although some of the early computers were decimal machines, modern computers are binary machines. That is, numbers within the computer are represented in binary form. In fact, all information is somehow represented using binary values. The reason is that each storage location within a computer contains either a low-voltage signal or a high-voltage signal. Because each location can have only one of two states, it is logical to equate those states to 0 and 1. A low-voltage signal is equated with a 0, and a high-voltage signal is equated with a 1. In fact, you can forget about voltages and think of each storage location as containing either a 0 or a 1. Note that a storage location cannot be empty: It must contain either a 0 or a 1.
Each storage unit is called a binary digit, or bit for short. Bits are grouped together into bytes (8 bits), and bytes are grouped together into units called words. The number of bits in a word is known as the word length of the computer. For example, IBM 370 architecture in the late 1970s had half words (2 bytes or 16 bits), full words (4 bytes), and double words (8 bytes). Modern computers are often 32-bit machines or 64-bit machines.
We have much more to explore about the relationship between computers and binary numbers. In the next chapter, we examine many kinds of data and see how they are represented in a computer. In Chapter 4, we see how to control electrical signals that represent binary values. In Chapter 6, we see how binary numbers are used to represent program commands that the computer executes.
SUMMARY
Numbers are written using positional notation, in which the digits are arranged in succession, the position of each digit has a place value, and the number is equal to the sum of the products of each digit by its place value. The place values are powers of the base of the number system. Thus, in the decimal number system, the place values are powers of 10; in the binary number system, the place values are powers of 2.
Arithmetic can be performed on numbers in any base represented in positional notation. The same operational rules apply to other bases as they do to base 10. Adding 1 to the largest digit in the base causes a carry into the next position.
Base 2, base 8, and base 16 are all related because these bases are powers of 2. This relationship provides a quick way to convert between numbers in these bases. Computer hardware is designed using numbers in base 2. A low-voltage signal is equated with 0, and a high-voltage signal is equated with 1.
KEY TERMS
EXERCISES
For Exercises 1–5, match the following numbers with their definition.
Number
Natural number
Integer number
Negative number
Rational number
For Exercises 6–11, match the solution with the problem.
10001100
10011110
1101010
1100000
1010001
1111000
For Exercises 12–17, mark the answers true or false as follows:
True
False
Exercises 18–47 are problems or short-answer questions.
-
45
69
1066
99
1
