3.2 Representing Numeric Data
Numeric values are the most prevalent type of data used in a computer system. Unlike with other types of data, there may seem to be no need to come up with a clever mapping between binary codes and numeric data. Because binary is a number system, a natural relationship exists between the numeric data and the binary values that we store to represent them. This is true, in general, for positive integer data. The basic issues regarding integer conversions were covered in Chapter 2 in the general discussion of the binary system and its equivalence to other bases. However, we have other issues regarding the representation of numeric data to consider at this point. Integers are just the beginning in terms of numeric data. This section discusses the representation of negative and noninteger values.
Representing Negative Values
Aren’t negative numbers just numbers with a minus sign in front? Perhaps. That is certainly one valid way to think about them. Let’s explore the issue of negative numbers and discuss appropriate ways to represent them on a computer.
Signed-Magnitude Representation
You have used the signed-magnitude representation of numbers since you first learned about negative numbers in grade school. In the traditional decimal system, a sign (+ or –) is placed before a number’s value, although the positive sign is often assumed. The sign represents the ordering, and the digits represent the magnitude of the number. The classic number line looks something like this, in which a negative sign means that the number is to the left of zero and the positive number is to the right of zero:

Performing addition and subtraction with signed integer numbers can be described as moving a certain number of units in one direction or another. To add two numbers, you find the first number on the scale and move in the direction of the sign of the second as many units as specified. Subtraction is done in a similar way, moving along the number line as dictated by the sign and the operation. In grade school, you soon graduated to doing addition and subtraction without using the number line.
There is a problem with the signed-magnitude representation: There are two representations of zero—plus zero and minus zero. The idea of a negative zero doesn’t necessarily bother us; we just ignore it. However, two representations of zero within a computer can cause unnecessary complexity, so other representations of negative numbers are used. Let’s examine another alternative.
Fixed-Sized Numbers
If we allow only a fixed number of values, we can represent numbers as just integer values, where half of them represent negative numbers. The sign is determined by the magnitude of the number. For example, if the maximum number of decimal digits we can represent is two, we can let 1 through 49 be the positive numbers 1 through 49 and let 50 through 99 represent the negative numbers –50 through –1. Let’s take the number line and number the negative values on the top according to this scheme:

To perform addition within this scheme, you just add the numbers together and discard any carry. Adding positive numbers should be okay. Let’s try adding a positive number and a negative number, a negative number and a positive number, and two negative numbers. These are shown in the following table in signed-magnitude and in this scheme (the carries are discarded):

What about subtraction, using this scheme for representing negative numbers? The key is in the relationship between addition and subtraction: A – B = A + (–B). We can subtract one number from another by adding the negative of the second to the first:
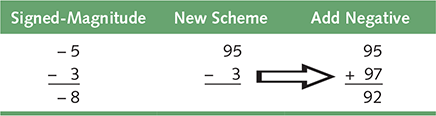
In this example, we have assumed a fixed size of 100 values and kept our numbers small enough to use the number line to calculate the negative representation of a number. However, you can also use a formula to compute the negative representation:
Negative(I) = 10k – I, where k is the number of digits
Let’s apply this formula to –3 in our two-digit representation:
–(3) = 102 – 3 = 97
What about a three-digit representation?
–(3) = 103 – 3 = 997
This representation of negative numbers is called the ten’s complement. Although humans tend to think in terms of sign and magnitude to represent numbers, the complement strategy is actually easier in some ways when it comes to electronic calculations. Because we store everything in a modern computer in binary, we use the binary equivalent of the ten’s complement, called the two’s complement.
Two’s Complement
Let’s assume that a number must be represented in eight bits: seven for the number and one for the sign. To more easily look at long binary numbers, we make the number line vertical:

Would the ten’s complement formula work with the 10 replaced by 2? That is, could we compute the negative binary representation of a number using the formula negative(I) = 2k – I? Let’s try it and see:
–(2) = 28 – 2 = 256 – 2 = 254
Decimal 254 is 11111110 in binary, which corresponds to the value –2 in the number line above. The leftmost bit, the sign bit, indicates whether the number is negative or positive. If the leftmost bit is 0, the number is positive; if it is 1, the number is negative. Thus, –(2) is 11111110.
There is an easier way to calculate the two’s complement: invert the bits and add 1. That is, take the positive value and change all the 1 bits to 0 and all the 0 bits to 1, and then add 1.

Addition and subtraction are accomplished the same way as in ten’s complement arithmetic:

With this representation, the leftmost bit in a negative number is always a 1. Therefore, you can tell immediately whether a binary number in two’s complement is negative or positive.
Number Overflow
Overflow occurs when the value that we compute cannot fit into the number of bits we have allocated for the result. For example, if each value is stored using eight bits, adding 127 to 3 would produce an overflow:
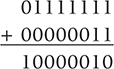
In our scheme, 10000010 represents –126, not +130. If we were not representing negative numbers, however, the result would be correct.
Overflow is a classic example of the type of problems we encounter by mapping an infinite world onto a finite machine. No matter how many bits we allocate for a number, there is always the potential need to represent a number that doesn’t fit. How overflow problems are handled varies by computer hardware and by the differences in programming languages.
Representing Real Numbers
In computing, we call all noninteger values (that can be represented) real values. For our purposes here, we define a real number as a value with a potential fractional part. That is, real numbers have a whole part and a fractional part, either of which may be zero. For example, some real numbers in base 10 are 104.32, 0.999999, 357.0, and 3.14159.
As we explored in Chapter 2, the digits represent values according to their position, and those position values are relative to the base. To the left of the decimal point, in base 10, we have the ones position, the tens position, the hundreds position, and so forth. These position values come from raising the base value to increasing powers (moving from the decimal point to the left). The positions to the right of the decimal point work the same way, except that the powers are negative. So the positions to the right of the decimal point are the tenths position (10–1 or one tenth), the hundredths position (10–2 or one hundredth), and so forth.
In binary, the same rules apply but the base value is 2. Since we are not working in base 10, the decimal point is referred to as a radix point, a term that can be used in any base. The positions to the right of the radix point in binary are the halves position (2–1 or one half), the quarters position (2–2 or one quarter), and so forth.
How do we represent a real value in a computer? We store the value as an integer and include information showing where the radix point is. That is, any real value can be described by three properties: the sign (positive or negative; the mantissa, which is made up of the digits in the value with the radix point assumed to be to the right; and the exponent, which determines how the radix point is shifted relative to the mantissa. A real value in base 10 can, therefore, be defined by the following formula:
sign * mantissa * 10exp
The representation is called floating point because the number of digits is fixed but the radix point floats. When a value is in floating-point form, a positive exponent shifts the decimal point to the right, and a negative exponent shifts the decimal point to the left.
Let’s look at how to convert a real number expressed in our usual decimal notation into floating-point notation. As an example, consider the number 148.69. The sign is positive, and two digits appear to the right of the decimal point. Thus the exponent is –2, giving us 14869 * 10–2. TABLE 3.1 shows other examples. For the sake of this discussion, we assume that only five digits can be represented.
| TABLE | |
| 3.1 Values in decimal notation and floating-point notation (five digits) | |
| Real Value | Floating-Point Value |
| 12001.00 | 12001 * 100 |
| –120.01 | –12001 * 10–2 |
| 0.12000 | 12000 * 10–5 |
| –123.10 | –12310 * 10–2 |
| 155555000.00 | 15555 * 104 |
© Artur Debat/Getty Images; © Alan Dyer/Stocktrek Images/Getty Images
How do we convert a value in floating-point form back into decimal notation? The exponent on the base tells us how many positions to move the radix point. If the exponent is negative, we move the radix point to the left. If the exponent is positive, we move the radix point to the right. Apply this scheme to the floating-point values in Table 3.1.
Notice that in the last example in Table 3.1, we lose information. Because we are storing only five digits to represent the significant digits (the mantissa), the whole part of the value is not accurately represented in floating-point notation.
Likewise, a binary floating-point value is defined by the following formula:
sign * mantissa * 2exp
Note that only the base value has changed. Of course, in this scheme the mantissa would contain only binary digits. To store a floating-point number in binary on a computer, we can store the three values that define it. For example, according to one common standard, if we devote 64 bits to the storage of a floating-point value, we use 1 bit for the sign, 11 bits for the exponent, and 52 bits for the mantissa. Internally, this format is taken into account whenever the value is used in a calculation or is displayed.
But how do we get the correct value for the mantissa if the value is not a whole number? In Chapter 2, we discussed how to change a natural number from one base to another. Here we have shown how real numbers are represented in a computer, using decimal examples. We know that all values are represented in binary in the computer. How do we change the fractional part of a decimal value to binary?
To convert a whole value from base 10 to another base, we divide by the new base, recording the remainder as the next digit to the left in the result and continuing to divide the quotient by the new base until the quotient becomes zero. Converting the fractional part is similar, but we multiply by the new base rather than dividing. The carry from the multiplication becomes the next digit to the right in the answer. The fractional part of the result is then multiplied by the new base. The process continues until the fractional part of the result is zero. Let’s convert .75 to binary.
.75 * 2 = 1.50
.50 * 2 = 1.00
Thus, .75 in decimal is .11 in binary. Let’s try another example.
.435 * 2 = 0.870
.870 * 2 = 1.740
.740 * 2 = 1.480
.480 * 2 = 0.960
.960 * 2 = 1.920
.920 * 2 = 1.840
...
Thus, .435 is 011011 . . . in binary. Will the fractional part ever become zero? Keep multiplying it out and see.
Now let’s go through the entire conversion process by converting 20.25 in decimal to binary. First we convert 20.
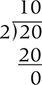

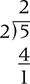

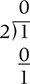
20 in binary is 10100. Now we convert the fractional part:
.25 * 2 = 0.50
.50 * 2 = 1.00
Thus 20.25 in decimal is 10100.01 in binary.
Scientific notation is a term with which you may already be familiar, so we mention it here. Scientific notation is a form of floating-point representation in which the decimal point is kept to the right of the leftmost digit. That is, there is one whole number. In many programming languages, if you print out a large real value without specifying how to print it, the value is printed in scientific notation. Because exponents could not be printed in early machines, an “E” was used instead. For example, “12001.32708” would be written as “1.200132708E+4” in scientific notation.
