2.2 Equilibrium Solutions and Stability

In previous sections we have often used explicit solutions of differential equations to answer specific numerical questions. But even when a given differential equation is difficult or impossible to solve explicitly, it often is possible to extract qualitative information about general properties of its solutions. For example, we may be able to establish that every solution x(t) grows without bound as t→+∞,t→+∞, or approaches a finite limit, or is a periodic function of t. In this section we introduce—mainly by consideration of simple differential equations that can be solved explicitly—some of the more important qualitative questions that can sometimes be answered for equations that are difficult or impossible to solve.

Example 1

Cooling and heating Let x(t) denote the temperature of a body with initial temperature x(0)=x0.x(0)=x0. At time t=0t=0 this body is immersed in a medium with constant temperature A. Assuming Newton’s law of cooling,

dxdt=−k(x−A)(k>0constant),
dxdt=−k(x−A)(k>0constant),
(1)

we readily solve (by separation of variables) for the explicit solution

x(t)=A+(x0−A)e−kt.
x(t)=A+(x0−A)e−kt.

It follows immediately that

limt→∞x(t)=A,
limt→∞x(t)=A,
(2)

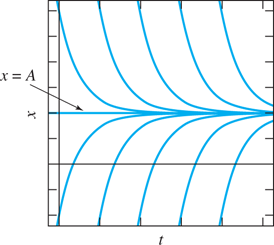
so the temperature of the body approaches that of the surrounding medium (as is evident to one’s intuition). Note that the constant function x(t)≡Ax(t)≡A is a solution of Eq. (1); it corresponds to the temperature of the body when it is in thermal equilibrium with the surrounding medium. In Fig. 2.2.1 the limit in (2) means that every other solution curve approaches the equilibrium solution curve x=Ax=A asymptotically as t→+∞.t→+∞.

FIGURE 2.2.1.

Typical solution curves for the equation of Newton’s law of cooling, dx/dt=−k(x−A)dx/dt=−k(x−A).

Remark

The behavior of solutions of Eq. (1) is summarized briefly by the phase diagram in Fig. 2.2.2—which indicates the direction (or “phase”) of change in x as a function of x itself. The right-hand side f(x)=−k(x−A)=k(A−x)f(x)=−k(x−A)=k(A−x) is positive if x<A,x<A, negative if x>A.x>A. This observation corresponds to the fact that solutions starting above the line x=Ax=A and those starting below it both approach the limiting solution x(t)≡Ax(t)≡A as t increases (as indicated by the arrows).

FIGURE 2.2.2.

Phase diagram for the equation dx/dt=f(x)=k(A−x)dx/dt=f(x)=k(A−x).

In Section 2.1 we introduced the general population equation

dxdt=(β−δ)x,
dxdt=(β−δ)x,
(3)

where ββ and δδ are the birth and death rates, respectively, in births or deaths per individual per unit of time. The question of whether a population x(t) is bounded or unbounded as t→+∞t→+∞ is of evident interest. In many situations—like the logistic and explosion/extinction populations of Section 2.1—the birth and death rates are known functions of x. Then Eq. (3) takes the form

dxdt=f(x).
dxdt=f(x).
(4)

This is an autonomous first-order differential equation—one in which the independent variable t does not appear explicitly (the terminology here stemming from the Greek word autonomos for “independent,” e.g., of the time t). As in Example 1, the solutions of the equation f(x)=0f(x)=0 play an important role and are called critical points of the autonomous differential equation dx/dt=f(x)dx/dt=f(x).

If x=cx=c is a critical point of Eq. (4), then the differential equation has the constant solution x(t)≡c.x(t)≡c. A constant solution of a differential equation is sometimes called an equilibrium solution (one may think of a population that remains constant because it is in “equilibrium” with its environment). Thus the critical point x=c,x=c, a number, corresponds to the equilibrium solution x(t)≡c,x(t)≡c, a constant-valued function.

Example 2 illustrates the fact that the qualitative behavior (as t increases) of the solutions of an autonomous first-order equation can be described in terms of its critical points.

Example 2

Logistic equation Consider the logistic differential equation

dxdt=kx(M−x)
dxdt=kx(M−x)
(5)

(with k>0k>0 and M>0M>0). It has two critical points—the solutions x=0x=0 and x=Mx=M of the equation

f(x)=kx(M−x)=0.
f(x)=kx(M−x)=0.

In Section 2.1 we discussed the logistic-equation solution

x(t)=Mx0x0+(M−x0)e−kMt
x(t)=Mx0x0+(M−x0)e−kMt
(6)

satisfying the initial condition x(0)=x0.x(0)=x0. Note that the initial values x0=0x0=0 and x0=Mx0=M yield the equilibrium solutions x(t)≡0x(t)≡0 and x(t)≡Mx(t)≡M of Eq. (5).

We observed in Section 2.1 that if x0>0,x0>0, then x(t)→Mx(t)→M as t→+∞.t→+∞. But if x0<0,x0<0, then the denominator in Eq. (6) initially is positive, but vanishes when

t=t1=1kMlnM−x0−x0>0.
t=t1=1kMlnM−x0−x0>0.

Because the numerator in (6) is negative in this case, it follows that

limt→t−1x(t)=−∞ifx0<0.
limt→t−1x(t)=−∞ifx0<0.

It follows that the solution curves of the logistic equation in (5) look as illustrated in Fig. 2.2.3. Here we see graphically that every solution either approaches the equilibrium solution x(t)≡Mx(t)≡M as t increases, or (in a visually obvious sense) diverges away from the other equilibrium solution x(t)≡0.x(t)≡0.

Stability of Critical Points

Figure 2.2.3 illustrates the concept of stability. A critical point x=cx=c of an autonomous first-order equation is said to be stable provided that, if the initial value x0x0 is sufficiently close to c, then x(t) remains close to c for all t>0.t>0. More precisely, the critical point c is stable if, for each ϵ>0,ϵ>0, there exists δ>0δ>0 such that

|x0−c|<δimplies that|x(t)−c|<ϵ
|x0−c|<δimplies that|x(t)−c|<ϵ
(7)

for all t>0.t>0. The critical point x=cx=c is unstable if it is not stable.

FIGURE 2.2.3.

Typical solution curves for the logistic equation dx/dt=kx(M−x)dx/dt=kx(M−x).

Figure 2.2.4 shows a “wider view” of the solution curves of a logistic equation with k=1k=1 and M=4.M=4. Note that the strip 3.5<x<4.53.5<x<4.5 enclosing the stable equilibrium curve x=4x=4 acts like a funnel—solution curves (moving from left to right) enter this strip and thereafter remain within it. By contrast, the strip −0.5<x<0.5−0.5<x<0.5 enclosing the unstable solution curve x=0x=0 acts like a spout—solution curves leave this strip and thereafter remain outside it. Thus the critical point x=Mx=M is stable, whereas the critical point x=0x=0 is unstable.

FIGURE 2.2.4.

Solution curves, funnel, and spout for dx/dt=4x−x2dx/dt=4x−x2.

Remark 1

We can summarize the behavior of solutions of the logistic equation in (5)—in terms of their initial values—by means of the phase diagram shown in Fig. 2.2.5. It indicates that x(t)→Mx(t)→M as t→+∞t→+∞ if either x0>Mx0>M or 0<x0<M,0<x0<M, whereas x(t)→−∞x(t)→−∞ as t increases if x0<0.x0<0. The fact that M is a stable critical point would be important, for instance, if we wished to conduct an experiment with a population of M bacteria. It is impossible to count precisely M bacteria for M large, but any initially positive population will approach M as t increases.

FIGURE 2.2.5.

Phase diagram for the logistic equation dx/dt=f(x)=kx(M−x)dx/dt=f(x)=kx(M−x).

Remark 2

Related to the stability of the limiting solution M=a/bM=a/b of the logistic equation

dxdt=ax−bx2
dxdt=ax−bx2
(8)

is the “predictability” of M for an actual population. The coefficients a and b are unlikely to be known precisely for an actual population. But if they are replaced with close approximations a⋆a⋆ and b⋆b⋆—derived perhaps from empirical measurements—then the approximate limiting population M⋆=a⋆/b⋆M⋆=a⋆/b⋆ will be close to the actual limiting population M=a/b.M=a/b. We may therefore say that the value M of the limiting population predicted by a logistic equation not only is a stable critical point of the differential equation, but this value also is “stable” with respect to small perturbations of the constant coefficients in the equation. (Note that one of these two statements involves changes in the initial value x0;x0; the other involves changes in the coefficients a and b.)

Example 3

Explosion/extinction Consider now the explosion/extinction equation

dxdt=kx(x−M)
dxdt=kx(x−M)
(9)

of Eq. (10) in Section 2.1. Like the logistic equation, it has the two critical points x=0x=0 and x=Mx=M corresponding to the equilibrium solutions x(t)≡0x(t)≡0 and x(t)≡M.x(t)≡M. According to Problem 33 in Section 2.1, its solution with x(0)=x0x(0)=x0 is given by

x(t)=Mx0x0+(M−x0)ekMt
x(t)=Mx0x0+(M−x0)ekMt
(10)

(with only a single difference in sign from the logistic solution in (6)). If x0<M,x0<M, then (because the coefficient of the exponential in the denominator is positive) it follows immediately from Eq. (10) that x(t)→0x(t)→0 as t→+∞.t→+∞. But if x0>M,x0>M, then the denominator in (10) initially is positive, but vanishes when

t=t1=1kMlnx0x0−M>0.
t=t1=1kMlnx0x0−M>0.

Because the numerator in (10) is positive in this case, it follows that

limt→t−1x(t)=+∞ifx0>M.
limt→t−1x(t)=+∞ifx0>M.

Therefore, the solution curves of the explosion/extinction equation in (9) look as illustrated in Fig. 2.2.6. A narrow band along the equilibrium curve x=0x=0 (as in Fig. 2.2.4) would serve as a funnel, while a band along the solution curve x=Mx=M would serve as a spout for solutions. The behavior of the solutions of Eq. (9) is summarized by the phase diagram in Fig. 2.2.7, where we see that the critical point x=0x=0 is stable and the critical point x=Mx=M is unstable.

FIGURE 2.2.6.

Typical solution curves for the explosion/extinction equation dx/dt=kx(x−M)dx/dt=kx(x−M).

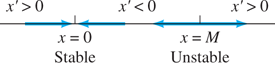
FIGURE 2.2.7.

Phase diagram for the explosion/extinction equation dx/dt=f(x)=kx(x−M)dx/dt=f(x)=kx(x−M).

Harvesting a Logistic Population

The autonomous differential equation

dxdt=ax−bx2−h
dxdt=ax−bx2−h
(11)

(with a, b, and h all positive) may be considered to describe a logistic population with harvesting. For instance, we might think of the population of fish in a lake from which h fish per year are removed by fishing.

Example 4

Threshold/limiting population Let us rewrite Eq. (11) in the form

dxdt=kx(M−x)−h,
dxdt=kx(M−x)−h,
(12)

which exhibits the limiting population M in the case h=0h=0 of no harvesting. Assuming hereafter that h>0,h>0, we can solve the quadratic equation −kx2+kMx−h=0−kx2+kMx−h=0 for the two critical points

H, N=kM±√(kM)2−4hk2k=12(M±√M2−4h/k),
H, N=kM±(kM)2−4hk−−−−−−−−−−√2k=12(M±M2−4h/k−−−−−−−−−√),
(13)

assuming that the harvesting rate h is sufficiently small that 4h<kM2,4h<kM2, so both roots H and N are real with 0<H<N<M.0<H<N<M. Then we can rewrite Eq. (12) in the form

dxdt=k(N−x)(x−H).
dxdt=k(N−x)(x−H).
(14)

For instance, the number of critical points of the equation may change abruptly as the value of a parameter is changed. In Problem 24 we ask you to solve this equation for the solution

x(t)=N(x0−H)−H(x0−N)e−k(N−H)t(x0−H)−(x0−N)e−k(N−H)t
x(t)=N(x0−H)−H(x0−N)e−k(N−H)t(x0−H)−(x0−N)e−k(N−H)t
(15)

in terms of the initial value x(0)=x0x(0)=x0.

Note that the exponent −k(N−H)t−k(N−H)t is negative for t>0.t>0. If x0>N,x0>N, then each of the coefficients within parentheses in Eq. (15) is positive; it follows that

Ifx0>Nthenx(t)→Nast→+∞.
Ifx0>Nthenx(t)→Nast→+∞.
(16)

In Problem 25 we ask you to deduce also from Eq. (15) that

IfH<x0<Nthenx(t)→Nast→+∞,whereas
IfH<x0<Nthenx(t)→Nast→+∞,whereas
(17)
ifx0<Hthenx(t)→−∞ast→t1
ifx0<Hthenx(t)→−∞ast→t1
(18)

for a positive value t1t1 that depends on x0.x0. It follows that the solution curves of Eq. (12)—still assuming that 4h<kM24h<kM2—look as illustrated in Fig. 2.2.8. (Can you visualize a funnel along the line x=Nx=N and a spout along the line x=Hx=H?) Thus the constant solution x(t)≡Nx(t)≡N is an equilibrium limiting solution, whereas x(t)≡Hx(t)≡H is a threshold solution that separates different behaviors—the population approaches N if x0>H,x0>H, while it becomes extinct because of harvesting if x0<H.x0<H. Finally, the stable critical point x=Nx=N and the unstable critical point x=Hx=H are illustrated in the phase diagram in Fig. 2.2.9.

FIGURE 2.2.8.

Typical solution curves for the logistic harvesting equation dx/dt=k(N−x)(x−H).dx/dt=k(N−x)(x−H).

FIGURE 2.2.9.

Phase diagram for the logistic harvesting equation dx/dt=f(x)=k(N−x)(x−H).dx/dt=f(x)=k(N−x)(x−H).

Example 5

Lake stocked with fish For a concrete application of our stability conclusions in Example 4, suppose that k=1k=1 and M=4M=4 for a logistic population x(t) of fish in a lake, measured in hundreds after t years. Without any fishing at all, the lake would eventually contain nearly 400 fish, whatever the initial population. Now suppose that h=3,h=3, so that 300 fish are “harvested” annually (at a constant rate throughout the year). Equation (12) is then dx/dt=x(4−x)−3,dx/dt=x(4−x)−3, and the quadratic equation

−x2+4x−3=(3−x)(x−1)=0
−x2+4x−3=(3−x)(x−1)=0

has solutions H=1H=1 and N=3.N=3. Thus the threshold population is 100 fish and the (new) limiting population is 300 fish. In short, if the lake is stocked initially with more than 100 fish, then as t increases, the fish population will approach a limiting value of 300 fish. But if the lake is stocked initially with fewer than 100 fish, then the lake will be “fished out” and the fish will disappear entirely within a finite period of time.

Bifurcation and Dependence on Parameters

A biological or physical system that is modeled by a differential equation may depend crucially on the numerical values of certain coefficients or parameters that appear in the equation. For instance, the number of critical points of the equation may change abruptly as the value of a parameter is changed.

Example 6

Critical/excessive harvesting The differential equation

dxdt=x(4−x)−h
dxdt=x(4−x)−h
(19)

(with x in hundreds) models the harvesting of a logistic population with k=1k=1 and limiting population M=4M=4 (hundred). In Example 5 we considered the case of harvesting level h=3,h=3, and found that the new limiting population is N=3N=3 hundred and the threshold population is H=1H=1 hundred. Typical solution curves, including the equilibrium solutions x(t)≡3x(t)≡3 and x(t)≡1,x(t)≡1, then look like those pictured in Fig. 2.2.8.

Now let’s investigate the dependence of this picture upon the harvesting level h. According to Eq. (13) with k=1k=1 and M=4,M=4, the limiting and threshold populations N and H are given by

H, N=12(4±√16−4h)=2±√4−h.
H, N=12(4±16−4h−−−−−−√)=2±4−h−−−−−√.
(20)

If h<4h<4—we can consider negative values of h to describe stocking rather than harvesting the fish—then there are distinct equilibrium solutions x(t)≡Nx(t)≡N and x(t)≡Hx(t)≡H with N>HN>H as in Fig. 2.2.8.

But if h=4,h=4, then Eq. (20) gives N=H=2,N=H=2, so the differential equation has only the single equilibrium solution x(t)≡2.x(t)≡2. In this case the solution curves of the equation look like those illustrated in Fig. 2.2.10. If the initial number x0x0 (in hundreds) of fish exceeds 2, then the population approaches a limiting population of 2 (hundred fish). However, any initial population x0<2x0<2 (hundred) results in extinction with the fish dying out as a consequence of the harvesting of 4 hundred fish annually. The critical point x=2x=2 might therefore be described as “semistable”—it looks stable on the side x>2x>2 where solution curves approach the equilibrium solution x(t)≡2x(t)≡2 as t increases, but unstable on the side x<2x<2 where solution curves instead diverge away from the equilibrium solution.

FIGURE 2.2.10.

Solution curves of the equation x′=x(4−x)−hx'=x(4−x)−h with critical harvesting h=4h=4.

If, finally, h>4,h>4, then the quadratic equation corresponding to (20) has no real solutions and the differential equation in (19) has no equilibrium solutions. The solution curves then look like those illustrated in Fig. 2.2.11, and (whatever the initial number of fish) the population dies out as a result of the excessive harvesting.

FIGURE 2.2.11.

Solution curves of the equation x′=x(4−x)−hx'=x(4−x)−h with excessive harvesting h=5h=5.

If we imagine turning a dial to gradually increase the value of the parameter h in Eq. (19), then the picture of the solution curves changes from one like Fig. 2.2.8 with h<4,h<4, to Fig. 2.2.10 with h=4,h=4, to one like Fig. 2.2.11 with h>4.h>4. Thus the differential equation has

  • two critical points if h<4h<4;

  • one critical point if h=4h=4;

  • no critical point if h>4h>4.

The value h=4h=4—for which the qualitative nature of the solutions changes as h increases—is called a bifurcation point for the differential equation containing the parameter h. A common way to visualize the corresponding “bifurcation” in the solutions is to plot the bifurcation diagram consisting of all points (h, c), where c is a critical point of the equation x′=x(4−x)+hx'=x(4−x)+h. For instance, if we rewrite Eq. (20) as

c=2±√4−h,(c−2)2=4−h,
c(c−2)2==2±4−h−−−−−√,4−h,

where either c=Nc=N or c=H,c=H, then we get the equation of the parabola that is shown in Fig. 2.2.12. This parabola is then the bifurcation diagram for our differential equation that models a logistic fish population with harvesting at the level specified by the parameter h.

FIGURE 2.2.12.

The parabola (c−2)2=4−h(c−2)2=4−h is the bifurcation diagram for the differential equation x′=x(4−x)−hx'=x(4−x)−h.

2.2 Problems

In Problems 1 through 12 first solve the equation f(x)=0f(x)=0 to find the critical points of the given autonomous differential equation dx/dt=f(x).dx/dt=f(x). Then analyze the sign of f(x) to determine whether each critical point is stable or unstable, and construct the corresponding phase diagram for the differential equation. Next, solve the differential equation explicitly for x(t) in terms of t. Finally, use either the exact solution or a computer-generated slope field to sketch typical solution curves for the given differential equation, and verify visually the stability of each critical point.

  1. dxdt=x−4dxdt=x−4

     

  2. dxdt=3−xdxdt=3−x

     

  3. dxdt=x2−4xdxdt=x2−4x

     

  4. dxdt=3x−x2dxdt=3x−x2

     

  5. dxdt=x2−4dxdt=x2−4

     

  6. dxdt=9−x2dxdt=9−x2

     

  7. dxdt=(x−2)2dxdt=(x−2)2

     

  8. dxdt=−(3−x)2dxdt=−(3−x)2

     

  9. dxdt=x2−5x+4dxdt=x2−5x+4

     

  10. dxdt=7x−x2−10dxdt=7x−x2−10

     

  11. dxdt=(x−1)3dxdt=(x−1)3

     

  12. dxdt=(2−x)3dxdt=(2−x)3

In Problems 13 through 18, use a computer system or graphing calculator to plot a slope field and/or enough solution curves to indicate the stability or instability of each critical point of the given differential equation. (Some of these critical points may be semistable in the sense mentioned in Example 6.)

  1. dxdt=(x+2)(x−2)2dxdt=(x+2)(x−2)2

     

  2. dxdt=x(x2−4)dxdt=x(x2−4)

     

  3. dxdt=(x2−4)2dxdt=(x2−4)2

     

  4. dxdt=(x2−4)3dxdt=(x2−4)3

     

  5. dxdt=x2(x2−4)dxdt=x2(x2−4)

     

  6. dxdt=x3(x2−4)dxdt=x3(x2−4)

     

  7. The differential equation dx/dt=110x(10−x)−hdx/dt=110x(10−x)−h models a logistic population with harvesting at rate h. Determine (as in Example 6) the dependence of the number of critical points on the parameter h, and then construct a bifurcation diagram like Fig. 2.2.12.

  8. The differential equation dx/dt=1100x(x−5)+sdx/dt=1100x(x−5)+s models a population with stocking at rate s. Determine the dependence of the number of critical points c on the parameter s, and then construct the corresponding bifurcation diagram in the sc-plane.

  9. Pitchfork bifurcation Consider the differential equation dx/dt=kx−x3.dx/dt=kx−x3. (a) If k≦0,k≦0, show that the only critical value c=0c=0 of x is stable. (b) If k>0,k>0, show that the critical point c=0c=0 is now unstable, but that the critical points c=±√kc=±k−−√ are stable. Thus the qualitative nature of the solutions changes at k=0k=0 as the parameter k increases, and so k=0k=0 is a bifurcation point for the differential equation with parameter k. The plot of all points of the form (k, c) where c is a critical point of the equation x′=kx−x3x'=kx−x3 is the “pitchfork diagram” shown in Fig. 2.2.13.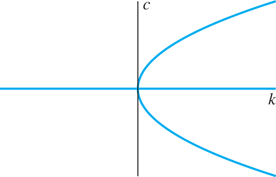

    FIGURE 2.2.13.

    Bifurcation diagram for dx/dt=kx−x3dx/dt=kx−x3.

  10. Consider the differential equation dx/dt=x+kx3dx/dt=x+kx3 containing the parameter k. Analyze (as in Problem 21) the dependence of the number and nature of the critical points on the value of k, and construct the corresponding bifurcation diagram.

  11. Variable-rate harvesting Suppose that the logistic equation dx/dt=kx(M−x)dx/dt=kx(M−x) models a population x(t) of fish in a lake after t months during which no fishing occurs. Now suppose that, because of fishing, fish are removed from the lake at the rate of hxhx fish per month (with h a positive constant). Thus fish are “harvested” at a rate proportional to the existing fish population, rather than at the constant rate of Example 4. (a) If 0<h<kM,0<h<kM, show that the population is still logistic. What is the new limiting population? (b) If h≧kM,h≧kM, show that x(t)→0x(t)→0 are t→+∞,t→+∞, so the lake is eventually fished out.

  12. Separate variables in the logistic harvesting equation dx/dt=k(N−x)(x−H)dx/dt=k(N−x)(x−H) and then use partial fractions to derive the solution given in Eq. (15).

  13. Use the alternative forms

    x(t)=N(x0 − H) + H(N − x0)e − k(N − H)t(x0 − H) + (N − x0)e − k(N − H)t=H(N − x0)e − k(N − H)t − N(H − x0)(N − x0)e − k(N − H)t − (H − x0)
    x(t)==N(x0 − H) + H(N − x0)e − k(N − H)t(x0 − H) + (N − x0)e − k(N − H)tH(N − x0)e − k(N − H)t − N(H − x0)(N − x0)e − k(N − H)t − (H − x0)

    of the solution in (15) to establish the conclusions stated in (17) and (18).

Constant-Rate Harvesting

Example 4 dealt with the case 4h>kM24h>kM2 in the equation dx/dt=kx(M−x)−hdx/dt=kx(M−x)−h that describes constant-rate harvesting of a logistic population. Problems 26 and 27 deal with the other cases.

  1. If 4h=kM2,4h=kM2, show that typical solution curves look as illustrated in Fig. 2.2.14. Thus if x0≧M/2,x0≧M/2, then x(t)→M/2x(t)→M/2 as t→+∞.t→+∞. But if x0<M/2,x0<M/2, then x(t)=0x(t)=0 after a finite period of time, so the lake is fished out. The critical point x=M/2x=M/2 might be called semistable, because it looks stable from one side, unstable from the other.

    FIGURE 2.2.14.

    Solution curves for harvesting a logistic population with 4h=kM24h=kM2.

  2. If 4h>kM2,4h>kM2, show that x(t)=0x(t)=0 after a finite period of time, so the lake is fished out (whatever the initial population). [Suggestion: Complete the square to rewrite the differential equation in the form dx/dt=−k[(x−a)2+b2].dx/dt=−k[(x−a)2+b2]. Then solve explicitly by separation of variables.] The results of this and the previous problem (together with Example 4) show that h=14kM2h=14kM2 is a critical harvesting rate for a logistic population. At any lesser harvesting rate the population approaches a limiting population N that is less than M (why?), whereas at any greater harvesting rate the population reaches extinction.

  3. Alligator population This problem deals with the differential equation dx/dt=kx(x−M)−hdx/dt=kx(x−M)−h that models the harvesting of an unsophisticated population (such as alligators). Show that this equation can be rewritten in the form dx/dt=k(x−H)(x−K),dx/dt=k(x−H)(x−K), where

    H=12(M+√M2+4h/k)>0,K=12(M−√M2+4h/k)<0.
    HK==12(M+M2+4h/k−−−−−−−−−√)>0,12(M−M2+4h/k−−−−−−−−−√)<0.

    Show that typical solution curves look as illustrated in Fig. 2.2.15.

  4. Consider the two differential equations

    dxdt=(x−a)(x−b)(x−c)
    dxdt=(x−a)(x−b)(x−c)
    (21)
    anddxdt=(a−x)(b−x)(c−x),
    anddxdt=(a−x)(b−x)(c−x),
    (22)

    each having the critical points a, b, and c; suppose that a<b<c.a<b<c. For one of these equations, only the critical point b is stable; for the other equation, b is the only unstable critical point. Construct phase diagrams for the two equations to determine which is which. Without attempting to solve either equation explicitly, make rough sketches of typical solution curves for each. You should see two funnels and a spout in one case, two spouts and a funnel in the other.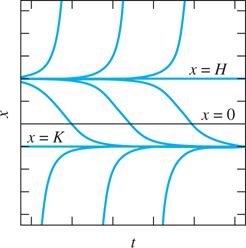

    FIGURE 2.2.15.

    Solution curves for harvesting a population of alligators.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.
Reset
18.219.102.189