Section 1.1

11. If $y = y_{1} = x^{- 2}$ $y = y_{1} = x^{- 2}$ , then $y ′ (x) = - 2 x^{- 3}$ $y ′ (x) = - 2 x^{- 3}$ and $y ″ (x) = 6 x^{- 4}$ $y ″ (x) = 6 x^{- 4}$ , so $x^{2} y ″ + 5 x y ′ + 4 y = x^{2} (6 x^{- 4}) + 5 x (- 2 x^{- 3}) + 4 (x^{- 2}) = 6 x^{- 2} - 10 x^{- 2} + 4 x^{- 2} = 0$ $x^{2} y ″ + 5 x y ′ + 4 y = x^{2} (6 x^{- 4}) + 5 x (- 2 x^{- 3}) + 4 (x^{- 2}) = 6 x^{- 2} - 10 x^{- 2} + 4 x^{- 2} = 0$ . If $y = y_{2} = x^{- 2} \ln x$ $y = y_{2} = x^{- 2} \ln x$ , then $y ′ (x) = x^{- 3} - 2 x^{- 3} \ln x$ $y ′ (x) = x^{- 3} - 2 x^{- 3} \ln x$ and $y ″ (x) = - 5 x^{- 4} + 6 x^{- 4} \ln x$ $y ″ (x) = - 5 x^{- 4} + 6 x^{- 4} \ln x$ , so $x^{2} y ″ + 5 x y ′ + 4 y = x^{2} (- 5 x^{- 4} + 6 x^{- 4} \ln x) + 5 x (x^{- 3} - 2 x^{- 3} \ln x) + 4 (x^{- 2} \ln x) = 0$ $x^{2} y ″ + 5 x y ′ + 4 y = x^{2} (- 5 x^{- 4} + 6 x^{- 4} \ln x) + 5 x (x^{- 3} - 2 x^{- 3} \ln x) + 4 (x^{- 2} \ln x) = 0$ .
13. $r = \frac{2}{3}$ $r = \frac{2}{3}$
14. $r = \pm \frac{1}{2}$ $r = \pm \frac{1}{2}$
15. $r = - 2$ $r = - 2$ , 1
16. $r = \frac{1}{6} (- 3 \pm \sqrt{57})$ $r = \frac{1}{6} (- 3 \pm \sqrt{57})$
17. $C = 2$ $C = 2$
18. $C = 3$ $C = 3$
19. $C = 6$ $C = 6$
20. $C = 11$ $C = 11$
21. $C = 7$ $C = 7$
22. $C = 1$ $C = 1$
23. $C = - 56$ $C = - 56$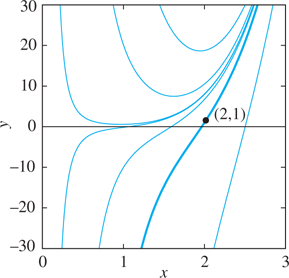
24. $C = 17$ $C = 17$
25. $C = π / 4$ $C = π / 4$
26. $C = - π$ $C = - π$
27. $y ′ = x + y$ $y ′ = x + y$
28. $y ′ = 2 y / x$ $y ′ = 2 y / x$
29. $y ′ = x / (1 - y)$ $y ′ = x / (1 - y)$
31. $y ′ = (y - x) / (y + x)$ $y ′ = (y - x) / (y + x)$
32. $d P / d t = k \sqrt{P}$ $d P / d t = k \sqrt{P}$
33. $d v / d t = k v^{2}$ $d v / d t = k v^{2}$
35. $d N / d t = k (P - N)$ $d N / d t = k (P - N)$
37. $y \equiv 1$ $y \equiv 1$ or $y = x$ $y = x$
39. $y = x^{2}$ $y = x^{2}$
41. $y = \frac{1}{2} e^{x}$ $y = \frac{1}{2} e^{x}$
42. $y = \cos x$ $y = \cos x$ or $y = \sin x$ $y = \sin x$
43. (b) The identically zero function $x (0) \equiv 0$ $x (0) \equiv 0$
44. (a) The graphs (figure below) of typical solutions with $k = \frac{1}{2}$ $k = \frac{1}{2}$ suggest that (for each) the value x(t) increases without bound as t increases.

(b) The graphs (figure below) of typical solutions with $k = - \frac{1}{2}$ $k = - \frac{1}{2}$ suggest that now the value x(t) approaches 0 as t increases without bound.
45. $P (t) = 100 / (50 - t)$ $P (t) = 100 / (50 - t)$ ; $P = 100$ $P = 100$ when $t = 49$ $t = 49$ , and $P = 1000$ $P = 1000$ when $t = 49.9$ $t = 49.9$ . Thus it appears that P(t) grows without bound as t approaches 50.
46. $v (t) = 50 / (5 + 2 t)$ $v (t) = 50 / (5 + 2 t)$ ; $v = 1$ $v = 1$ when $t = 22.5$ $t = 22.5$ , and $v = \frac{1}{10}$ $v = \frac{1}{10}$ when $t = 247.5$ $t = 247.5$ . Thus it appears that v(t) approaches 0 as t increases without bound.
47. (a) $C = 10.1$ $C = 10.1$ ; (b) No such C, but the constant function $y (x) \equiv 0$ $y (x) \equiv 0$ satisfies the conditions $y ′ = y^{2}$ $y ′ = y^{2}$ and $y (0) = 0$ $y (0) = 0$ .