4 Vector Spaces
4.1 The Vector Space R3
Here we take a fresh look—from the viewpoint of linear algebra—at the familiar 3-dimensional space of the physical world around us (and of multivariable calculus). This review, combining old and new ideas, will provide an introduction to basic concepts that are explored further in subsequent sections of the chapter.
We define three-dimensional coordinate space R3
The location of the point P can also be specified by means of the arrow or directed line segment (Fig. 4.1.1) that points from the origin (its initial point) to P (its terminal point). Arrows are often used in physics to represent vector quantities, such as force and velocity, that possess both magnitude and direction. For instance, the velocity vector v of a point moving in space may be represented by an arrow that points in the direction of its motion, with the length of the arrow being equal to the speed of the moving point. If we locate this arrow with its initial point at the origin O, then its direction and length are determined by its terminal point (a, b, c). But the arrow is merely a pictorial object; the mathematical object associated with the vector v is simply the point (a, b, c). For this reason, it is customary to use the words point and vector interchangeably for elements of 3-space R3
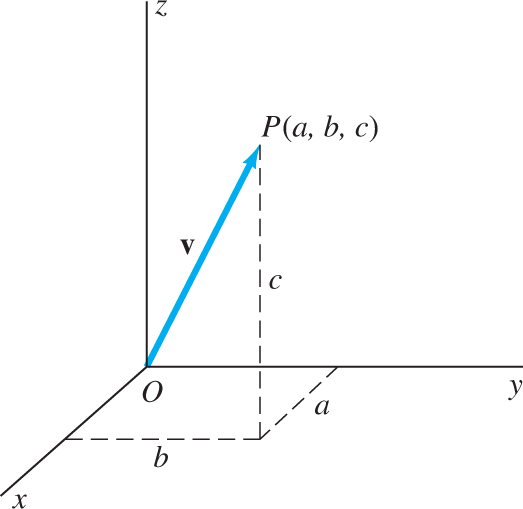
FIGURE 4.1.1.
The arrow →OP
Thus “a vector is a point is a vector,” but vector terminology often aids us in visualizing geometric relationships between different points. The point P(a, b, c) determines the vector v=(a,b,c)
As in Section 3.4, we adopt the convention that the vector v with components v1, v2
with the column matrix regarded as just another symbol representing one and the same ordered triple of real numbers. Then the following definitions of addition of vectors and of multiplication of vectors by scalars are consistent with the matrix operations defined in Section 3.4.
Thus we add vectors by adding corresponding components—that is, by componentwise addition (just as we add matrices). For instance, the sum of the vectors u=(4,3,−5)
The geometric representation of vectors as arrows often converts an algebraic relation into a picture that is readily understood and remembered. Addition of vectors is defined algebraically by Eq. (1). The geometric interpretation of vector addition is the triangle law of addition illustrated in Fig. 4.1.2 (for the case of 2-dimensional vectors in the plane), where the labeled lengths indicate why this interpretation is valid. An equivalent interpretation is the parallelogram law of addition, illustrated in Fig. 4.1.3.

FIGURE 4.1.2.
The triangle law of vector addition.

FIGURE 4.1.3.
The parallelogram law of vector addition.
Multiplication of a vector by a scalar (a real number) is also defined in a componentwise manner.
The length |v|
The length of cv is |c|
The geometric interpretation of scalar multiplication is that cv is a vector of length |c|⋅|v|

FIGURE 4.1.4.
The vector cu may have the same direction as u or the opposite direction.
With vector addition and multiplication by scalars defined as in (1) and (2), R3
Of course, 0=(0,0,0)
so we have verified property (e).
The Vector Space R2
The familiar coordinate plane R2
Clearly, the sum of any two vectors in R2
The two vectors u and v are collinear—they lie on the same line through the origin and hence point either in the same direction (Fig. 4.1.5) or in opposite directions—if and only if one is a scalar multiple of the other; that is, either
for some scalar c. The scalar c merely adjusts the length and direction of one vector to fit the other. If u and v are nonzero vectors, then c=±|u|/|v|

FIGURE 4.1.5.
Two linearly dependent vectors u and v.
If one of the relations in (4) holds for some scalar c, then we say that the two vectors are linearly dependent. Note that if u=0
If u and v are linearly dependent vectors with u=cv
Conversely, suppose that Eq. (5) holds with a and b not both zero. If a≠0
with c=−b/a
The most interesting pairs of vectors are those that are not linearly dependent. The two vectors u and v are said to be linearly independent provided that they are not linearly dependent. Thus u and v are linearly independent if and only if neither is a scalar multiple of the other. By Theorem 2 this is equivalent to the following statement:
Thus the vectors u and v are linearly independent provided that no nontrivial linear combination of them is equal to the zero vector.
Example 1
If u=(3,−2),v=(−6,4),
Then
and thus we get the simultaneous equations
It is now easy to show that a=b=0
it follows that a=b=0
Alternatively, we could prove that u and w are linearly independent by showing that neither is a scalar multiple of the other (because 53≠72
The most important property of linearly independent pairs of plane vectors is this: If u and v are linearly independent vectors in the plane, then any third vector w in R2

FIGURE 4.1.6.
The vector w as a linear combination of the two linearly independent vectors u and v.
Example 2
Express the vector w=(11,4)
Solution
We want to find numbers a and b such that au+bv=w
This vector equation is equivalent to the 2×2
which (using Gaussian elimination or Cramer’s rule) we readily solve for a=5, b=2
Linear Independence in R3
We have said that the two vectors are linearly dependent provided that they lie on the same line through the origin. For three vectors u=(u1,u2,u3), v=(v1,v2,v3)
Note that each of the three equations in (6) implies that there exist three scalars a, b, and c not all zero such that
For if w=ru+sv
so we can take a=r, b=s
with r=−a/c
The three vectors u, v, and w are called linearly independent provided that they are not linearly dependent. Thus u, v, and w are linearly independent if and only if neither of them is a linear combination of the other two. As a consequence of Theorem 3, this is equivalent to the following statement:
Thus the three vectors u, v, and w are linearly independent provided that no nontrivial linear combination of them is equal to the zero vector.
Given two vectors, we can see at a glance whether either is a scalar multiple of the other. By contrast, it is not evident at a glance whether or not three given vectors in R3
Hence, in order to determine whether or not three given vectors u, v, and w are linearly independent, we can calculate the determinant in (8). In practice, however, it is usually more efficient to set up and solve the linear system in (9). If we obtain only the trivial solution a=b=c=0
Example 3
To determine whether the three vectors u=(1,2,−3), v=(3,1,−2)
By Gaussian elimination, we readily reduce this system to the echelon form
Therefore, we can choose c=1
and hence u, v, and w are linearly dependent, with w=−4u+3v
Basis Vectors in R3
Perhaps the most familiar triple of linearly independent vectors in R3
When represented by arrows with the initial points at the origin, these three vectors point in the positive directions along the three coordinate axes (Fig. 4.1.7). The expression
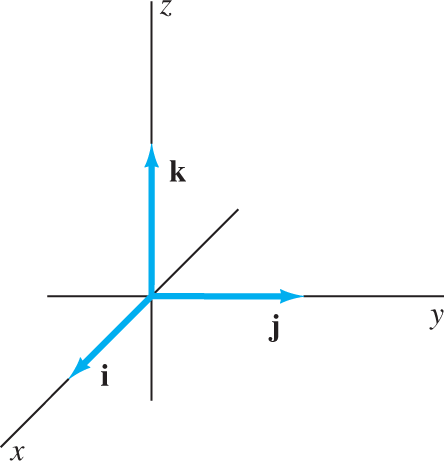
FIGURE 4.1.7.
The basic unit vectors i, j, and k.
shows both that
the three vectors i, j, and k are linearly independent (because v=0
v=0 immediately implies a=b=c=0a=b=c=0 ), and thatany vector in R3
R3 can be expressed as a linear combination of i, j, and k.
A basis for R3
of them. That is, given any vector t in R3
Example 4
In order to express the vector t=(4,20,23)
that we obtain by substitution in Eq. (12). The echelon form found by Gaussian elimination is
so c=3, b=4−2c=−2
Subspaces of R3
Up until this point, we have used the words line and plane only in an informal or intuitive way. It is now time for us to say precisely what is meant by a line or plane through the origin in R3
The nonempty subset V of R3
If u and v are vectors in V, then u+v
u+v is also in V (closure under addition).If u is a vector in V and c is a scalar, then cu is in V (closure under multiplication by scalars).
It is immediate that V=R3
Now we want to show that the proper subspaces of R3
Case 1: Suppose that V does not contain two linearly independent vectors. If u is a fixed nonzero vector in V, then, by condition (ii) above, every scalar multiple cu is also in V. Conversely, if v is any other vector in V, then u and v are linearly dependent, so it follows that v=cu

FIGURE 4.1.8.
The line L spanned by the vector u.
Case 2: Suppose that V contains two linearly independent vectors u and v. It then follows from conditions (i) and (ii) that V contains every linear combination au+bv

FIGURE 4.1.9.
The plane P spanned by the vectors u and v.
Subspaces of the coordinate plane R2
Example 5
Let V be the set of all vectors (x, y) in R2
Example 6
Let V be the set of all vectors (x, y) in R2
Example 6 illustrates the fact that lines that do not pass through the origin are not subspaces of R2
4.1 Problems
In Problems 1–4, find |a−b|, 2a+b
a=(2,5,−4), b=(1,−2,−3)
a=(2,5,−4), b=(1,−2,−3) a=(−1,0,2), b=(3,4,−5)
a=(−1,0,2), b=(3,4,−5) a=2i−3j+5k, b=5i+3j−7k
a=2i−3j+5k, b=5i+3j−7k a=2i−j, b=j−3k
a=2i−j, b=j−3k
In Problems 5–8, determine whether the given vectors u and v are linearly dependent or linearly independent.
u=(0,2), v=(0,3)
u=(0,2), v=(0,3) u=(0,2), v=(3,0)
u=(0,2), v=(3,0) u=(2,2), v=(2,−2)
u=(2,2), v=(2,−2) u=(2,−2), v=(−2,2)
u=(2,−2), v=(−2,2)
In Problems 9–14, express w as a linear combination of u and v.
u=(1,−2), v=(−1,3), w=(1,0)
u=(1,−2), v=(−1,3), w=(1,0) u=(3,4), v=(2,3), w=(0,−1)
u=(3,4), v=(2,3), w=(0,−1) u=(5,7), v=(2,3), w=(1,1)
u=(5,7), v=(2,3), w=(1,1) u=(4,1), v=(−2,−1), w=(2,−2)
u=(4,1), v=(−2,−1), w=(2,−2) u=(7,5), v=(3,4), w=(5,−2)
u=(7,5), v=(3,4), w=(5,−2) u=(5,−2), v=(−6,4), w=(5,6)
u=(5,−2), v=(−6,4), w=(5,6)
In Problems 15–18, apply Theorem 4 (that is, calculate a determinant) to determine whether the given vectors u, v, and w are linearly dependent or independent.
u=(3,−1,2), v=(5,4,−6), w=(8,3,−4)
u=(3,−1,2), v=(5,4,−6), w=(8,3,−4) u=(5,−2,4), v=(2,−3,5), w=(4,5,−7)
u=(5,−2,4), v=(2,−3,5), w=(4,5,−7) u=(1,−1,2), v=(3,0,1), w=(1,−2,2)
u=(1,−1,2), v=(3,0,1), w=(1,−2,2) u=(1,1,0), v=(4,3,1), w=(3,−2,−4)
u=(1,1,0), v=(4,3,1), w=(3,−2,−4)
In Problems 19–24, use the method of Example 3 to determine whether the given vectors u, v, and w are linearly independent or dependent. If they are linearly dependent, find scalars a, b, and c not all zero such that au+bv+cw=0
u=(2,0,1), v=(−3,1,−1), w=(0,−2,−1)
u=(2,0,1), v=(−3,1,−1), w=(0,−2,−1) u=(5,5,4), v=(2,3,1), w=(4,1,5)
u=(5,5,4), v=(2,3,1), w=(4,1,5) u=(1,1,−2), v=(−2,−1,6), w=(3,7,2)
u=(1,1,−2), v=(−2,−1,6), w=(3,7,2) u=(1,1,0), v=(5,1,3), w=(0,1,2)
u=(1,1,0), v=(5,1,3), w=(0,1,2) u=(2,0,3), v=(5,4,−2), w=(2,−1,1)
u=(2,0,3), v=(5,4,−2), w=(2,−1,1) u=(1,4,5), v=(4,2,5), w=(−3,3,−1)
u=(1,4,5), v=(4,2,5), w=(−3,3,−1)
In Problems 25–28, express the vector t as a linear combination of the vectors u, v, and w.
t=(2,−7,9), u=(1,−2,2), v=(3,0,1), w=(1,−1,2)
t=(2,−7,9), u=(1,−2,2), v=(3,0,1), w=(1,−1,2) t=(5,30,−21), u=(5,2,−2), v=(1,5,−3)
t=(5,30,−21), u=(5,2,−2), v=(1,5,−3) , w=(5,−3,4)w=(5,−3,4) t=(0,0,19), u=(1,4,3), v=(−1,−2,2), w=(4,4,1)
t=(0,0,19), u=(1,4,3), v=(−1,−2,2), w=(4,4,1) t=(7,7,7), u=(2,5,3), v=(4,1,−1), w=(1,1,5)
t=(7,7,7), u=(2,5,3), v=(4,1,−1), w=(1,1,5)
In Problems 29–32, show that the given set V is closed under addition and under multiplication by scalars and is therefore a subspace of R3
V is the set of all (x, y, z) such that x=0
x=0 .V is the set of all (x, y, z) such that x+y+z=0
x+y+z=0 .V is the set of all (x, y, z) such that 2x=3y
2x=3y .V is the set of all (x, y, z) such that z=2x+3y
z=2x+3y .
In Problems 33–36, show that the given set V is not a subspace of R3
V is the set of all (x, y, z) such that y=1
y=1 .V is the set of all (x, y, z) such that x+y+z=3
x+y+z=3 .V is the set of all (x, y, z) such that z≥0
z≥0 .V is the set of all (x, y, z) such that xyz=1
xyz=1 .Show that every subspace V of R3
R3 contains the zero vector 0.Suppose that V is a subspace of R3
R3 . Show that V is closed under the operation of taking linear combinations of pairs of vectors. That is, show that if u and v are in V and a and b are scalars, then au+bvau+bv is in V.Suppose that V is a proper subspace of R2
R2 and that u is a nonzero vector in V. Show that V is the set of all scalar multiples of u and therefore that V is a line through the origin.Suppose that u, v, and w are vectors in R3
R3 such that u and v are linearly independent but u, v, and w are linearly dependent. Show that there exist scalars a and b such that w=au+bvw=au+bv .Let V1
V1 and V2V2 be subspaces of R3R3 . Their intersection V=V1∩V2V=V1∩V2 is the set of all vectors that lie both in V1V1 and in V2V2 . Show that V is a subspace of R3R3 .
