Section 9.2

1. Asymptotically stable node
2. Unstable improper node
3. Unstable saddle point
4. Unstable saddle point
5. Asymptotically stable node
6. Unstable node
7. Unstable spiral point
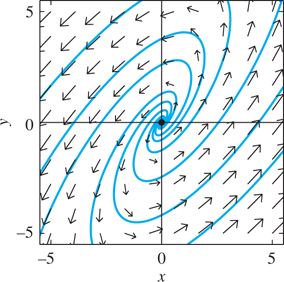
8. Asymptotically stable spiral point
9. Stable, but not asymptotically stable, center
10. Stable, but not asymptotically stable, center
11. Asymptotically stable node: (2, 1)
12. Unstable improper node: $(2, - 3)$ $(2, - 3)$
13. Unstable saddle point: (2, 2)
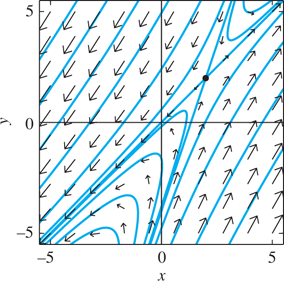
14. Unstable saddle point: (3, 4)
15. Asymptotically stable spiral point: (1, 1)
16. Unstable spiral point: (3, 2)
17. Stable center: $(\frac{5}{2}, - \frac{1}{2})$ $(\frac{5}{2}, - \frac{1}{2})$
18. Stable, but not asymptotically stable, center: $(- 2, - 1)$ $(- 2, - 1)$
19. (0, 0) is a stable node. Also, there is a saddle point at (0.67, 0.40).
20. (0, 0) is an unstable node. Also, there is a saddle point at $(- 1, - 1)$ $(- 1, - 1)$ and a spiral sink at $(- 2.30, - 1.70)$ $(- 2.30, - 1.70)$ .
21. (0, 0) is an unstable saddle point. Also, there is a spiral sink at $(- 0.51, - 2.12)$ $(- 0.51, - 2.12)$ .
22. (0, 0) is an unstable saddle point. Also, there are nodal sinks at $(\pm 0.82, \pm 5.06)$ $(\pm 0.82, \pm 5.06)$ and nodal sources at $(\pm 3.65, \mp 0.59)$ $(\pm 3.65, \mp 0.59)$ .
23. (0, 0) is a spiral sink. Also, there is a saddle point at $(- 1.08, - 0.68)$ $(- 1.08, - 0.68)$ .
24. (0, 0) is a spiral source. No other critical points are visible.
25. Theorem 2 implies only that (0, 0) is a stable sink—either a node or a spiral point. The phase portrait for $- 5 \leq x, y \leq 5$ $- 5 \leq x, y \leq 5$ also shows a saddle point at $(0.74, - 3.28)$ $(0.74, - 3.28)$ and spiral sink at $(2.47, - 0.46)$ $(2.47, - 0.46)$ . The origin looks like a nodal sink in a second phase portrait for $- 0.2 \leq x, y \leq 0.2,$ $- 0.2 \leq x, y \leq 0.2,$ which also reveals a second saddle point at (0.12, 0.07).
26. Theorem 2 implies only that (0, 0) is an unstable source. The phase portrait for $- 3 \leq x, y \leq 3$ $- 3 \leq x, y \leq 3$ also shows saddle points at (0.20, 0.25) and $(- 0.23, - 1.50),$ $(- 0.23, - 1.50),$ as well as a nodal sink at (2.36, 0.58).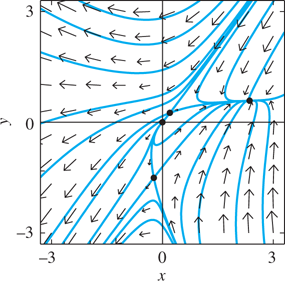
27. Theorem 2 implies only that (0, 0) is a center or a spiral point, but does not establish its stability. The phase portrait for $- 2 \leq x, y \leq 2$ $- 2 \leq x, y \leq 2$ also shows saddle points at $(- 0.25, - 0.51)$ $(- 0.25, - 0.51)$ and $(- 1.56, 1.64),$ $(- 1.56, 1.64),$ plus a nodal sink at $(- 1.07, - 1.20)$ $(- 1.07, - 1.20)$ . The origin looks like a likely center in a second phase portrait for $- 0.6 \leq x, y \leq 0.6$ $- 0.6 \leq x, y \leq 0.6$ .
28. Theorem 2 implies only that (0, 0) is a center or a spiral point, but does not establish its stability (though in the phase portrait it looks like a likely center). The phase portrait for $- 0.25 \leq x \leq 0.25, - 1 \leq y \leq 1$ $- 0.25 \leq x \leq 0.25, - 1 \leq y \leq 1$ also shows saddle points at (0.13, 0.63) and $(- 0.12, - 0.47)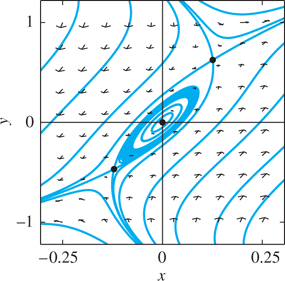$ $(- 0.12, - 0.47)$ .
29. There is a saddle point at (0, 0). The other critical point (1, 1) is indeterminate, but looks like a center in the phase portrait.
30. There is a saddle point at (1, 1) and a spiral sink at $(- 1, 1)$ $(- 1, 1)$ .
31. There is a saddle point at (1, 1) and a spiral sink at $(- 1, - 1)$ $(- 1, - 1)$ .
32. There is a saddle point at (2, 1) and a spiral sink at $(- 2, - 1)$ $(- 2, - 1)$ .
37. Note that the differential equation is homogeneous.