Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

9.4 Nonlinear Mechanical Systems

Now we apply the qualitative methods of Sections 9.1 and 9.2 to the analysis of simple mechanical systems like the mass-on-a-spring system shown in Fig. 9.4.1. Let m denote the mass in a suitable system of units and let x(t) denote the displacement of the mass at time t from its equilibrium position (in which the spring is unstretched). Previously we have always assumed that the force F(x) exerted by the spring on the mass is a linear function of x: F(x)=−kx $F (x) = - k x$ (Hooke’s law). In reality, however, every spring in nature actually is nonlinear (even if only slightly so). Moreover, springs in some automobile suspension systems deliberately are designed to be nonlinear. Here, then, we are interested specifically in the effects of nonlinearity.

So now we allow the force function F(x) to be nonlinear. Because F(0)=0 $F (0) = 0$ at the equilibrium position x=0, $x = 0,$ we may assume that F has a power series expansion of the form

F (x) = - k x + α x 2 + β x 3 + \dots .

$F (x) = - k x + α x^{2} + β x^{3} + \dots .$ (1)

We take k>0 $k > 0$ so that the reaction of the spring is directed opposite to the displacement when x is sufficiently small. If we assume also that the reaction of the spring is symmetric with respect to positive and negative displacements by the same distance, then F(−x)=−F(x), $F (- x) = - F (x),$ so F is an odd function. In this case it follows that the coefficient of xn $x^{n}$ in Eq. (1) is zero if n is even, so the first nonlinear term is the one involving x3. $x^{3} .$

For a simple mathematical model of a nonlinear spring we therefore take

F (x) = - k x + β x 3,

$F (x) = - k x + β x^{3},$ (2)

ignoring all terms in Eq. (1) of degree greater than 3. The equation of motion of the mass m is then

m x'' = - k x + β x 3 .

$m x ″ = - k x + β x^{3} .$ (3)

The Position–Velocity Phase Plane

If we introduce the velocity

y (t) = x' (t)

$y (t) = x ′ (t)$ (4)

of the mass with position x(t), then we get from Eq. (3) the equivalent first-order system

d x d t m d y d t = = y, - k x + β x 3 .

$\begin{array}{rcl} \frac{d x}{d t} & = & y, \\ m \frac{d y}{d t} & = & - k x + β x^{3} . \end{array}$ (5)

A phase plane trajectory of this system is a position-velocity plot that illustrates the motion of the mass on the spring. We can solve explicitly for the trajectories of this system by writing

d y d x = d y / d t d x / d t = - k x + β x 3 m y,

$\frac{d y}{d x} = \frac{d y / d t}{d x / d t} = \frac{- k x + β x^{3}}{m y},$

whence

m y d y + (k x - β x 3) d x = 0.

$m y d y + (k x - β x^{3}) d x = 0.$

Integration then yields

1 2 m y 2 + 1 2 k x 2 - 1 4 β x 4 = E

$\frac{1}{2} m y^{2} + \frac{1}{2} k x^{2} - \frac{1}{4} β x^{4} = E$ (6)

for the equation of a typical trajectory. We write E for the arbitrary constant of integration because KE=12my2 $K E = \frac{1}{2} m y^{2}$ is the kinetic energy of the mass with velocity y, and it is natural to define

P E = 1 2 k x 2 - 1 4 β x 4

$P E = \frac{1}{2} k x^{2} - \frac{1}{4} β x^{4}$ (7)

as the potential energy of the spring. Then Eq. (6) takes the form KE+PE=E, $K E + P E = E,$ so the constant E turns out to be the total energy of the mass-spring system. Equation (6) then expresses conservation of energy for the undamped motion of a mass on a spring.

The behavior of the mass depends on the sign of the nonlinear term in Eq. (2). The spring is called

hard if β<0 $β < 0$ ,
soft if β>0 $β > 0$ .

We consider the two cases separately.

Hard Spring Oscillations: If β<0, $β < 0,$ then the second equation in (5) takes the form my'=−x(∣∣β∣∣x2+k), $m y ′ = - x (| β | x^{2} + k),$ so it follows that the only critical point of the system is the origin (0, 0). Each trajectory

1 2 m y 2 + 1 2 k x 2 - 1 4 ∣ ∣ ∣ β ∣ ∣ ∣ x 4 = E > 0

$\frac{1}{2} m y^{2} + \frac{1}{2} k x^{2} - \frac{1}{4} | β | x^{4} = E > 0$ (8)

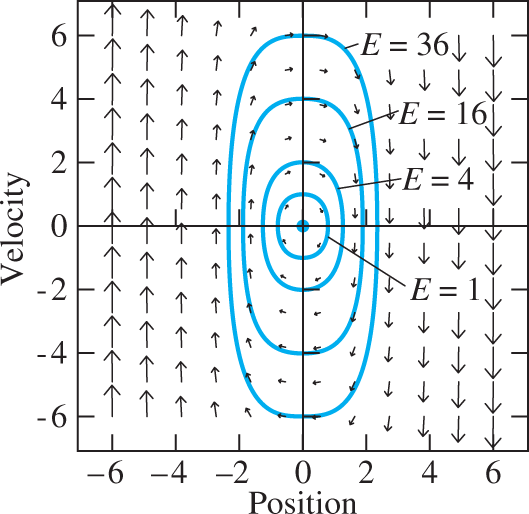
is an oval closed curve like those shown in Fig. 9.4.2, and thus (0, 0) is a stable center. As the point (x(t), y(t)) traverses a trajectory in the clockwise direction, the position x(t) and velocity y(t) of the mass oscillate alternately, as illustrated in Fig. 9.4.3. The mass is moving to the right (with x increasing) when y>0, $y > 0,$ to the left when y<0. $y < 0 .$ Thus the behavior of a mass on a nonlinear hard spring resembles qualitatively that of a mass on a linear spring with β=0 $β = 0$ (as in Example 3 of Section 9.1). But one difference between the linear and nonlinear situations is that, whereas the period T=2πm/k−−−−√ $T = 2 π \sqrt{m / k}$ of oscillation of a mass on a linear spring is independent of the initial conditions, the period of a mass on a nonlinear spring depends on its initial position x(0) and initial velocity y(0) (Problems 21 through 26).

FIGURE 9.4.2.

Position-velocity phase plane portrait for the hard mass-and-spring system with m=k=2 $m = k = 2$ and β=−4<0 $β = - 4 < 0$ .

FIGURE 9.4.3.

Position and velocity solution curves for the hard mass-and-spring system with m=k=2 $m = k = 2$ and β=−4<0 $β = - 4 < 0$ .

Remark

The hard spring equation mx''=−kx−∣∣β∣∣x3 $m x ″ = - k x - | β | x^{3}$ has equivalent first-order system

x' = y, y' = - k m x - | β | m x 3

$x^{′} = y, y^{′} = - \frac{k}{m} x - \frac{| β |}{m} x^{3}$

with Jacobian matrix

J (x, y) = ⎡ ⎣ ⎢ 0 - k m - 3 | β | m x 2 10 ⎤ ⎦ ⎥, so J (0, 0) = [0 - ω 2 10]

$J (x, y) = [\begin{array}{c} 0 & 1 \\ - \frac{k}{m} - \frac{3 | β |}{m} x^{2} & 0 \end{array}], so J (0, 0) = [\begin{array}{c} 0 & 1 \\ - ω^{2} & 0 \end{array}]$

(writing k/m=ω2 $k / m = ω^{2}$ as usual). The latter matrix has characteristic equation λ2+ω2=0 $λ^{2} + ω^{2} = 0$ and pure imaginary eigenvalues λ1, λ2=±ωi. $λ_{1}, λ_{2} = \pm ω i .$ Thus the linearized system x'=y, y'=−ω2x $x ′ = y, y ′ = - ω^{2} x$ has a stable center at the critical point (0, 0)—as we observed in Example 4 of Section 9.1. However, the nonlinear cubic term in the differential equation has (in effect) replaced the elliptical trajectories (as in Fig. 9.1.8) of the linear system with the “flatter” quartic ovals we see in Fig. 9.4.2.

Soft Spring Oscillations: If β>0, $β > 0,$ then the second equation in (5) takes the form my'=x(βx2−k), $m y ′ = x (β x^{2} - k),$ so it follows that the system has the two critical points (±k/β−−−√,0) $(\pm \sqrt{k / β}, 0)$ in addition to the critical point (0, 0). These three critical points yield the only solutions for which the mass can remain at rest. The following example illustrates the greater range of possible behaviors of a mass on a soft spring.

Example 1

Undamped soft spring If m=1, k=4, $m = 1, k = 4,$ and β=1, $β = 1,$ then the equation of motion of the mass is

d 2 x d t 2 + 4 x - x 3 = 0,

$\frac{d^{2} x}{d t^{2}} + 4 x - x^{3} = 0,$ (9)

and Eq. (6) gives the trajectories in the form

1 2 y 2 + 2 x 2 - 1 4 x 4 = E .

$\frac{1}{2} y^{2} + 2 x^{2} - \frac{1}{4} x^{4} = E .$ (10)

After solving for

y = \pm 2 E - 4 x 2 + 1 2 x 4 - - - - - - - - - - - - - \sqrt,

$y = \pm \sqrt{2 E - 4 x^{2} + \frac{1}{2} x^{4}},$ (10′)

we could select a fixed value of the constant energy E and plot manually a trajectory like one of those shown in the computer-generated position-velocity phase plane portrait in Fig. 9.4.4.

The different types of phase plane trajectories correspond to different values of the energy E. If we substitute x=±k/β−−−√ $x = \pm \sqrt{k / β}$ and y=0 $y = 0$ into (6), we get the energy value E=k2/(4β)=4 $E = k^{2} / (4 β) = 4$ (because k=4 $k = 4$ and β=1 $β = 1$ ) that corresponds to the trajectories that intersect the x-axis at the nontrivial critical points (−2,0) $(- 2, 0)$ and (2, 0). These emphasized trajectories are called separatrices because they separate phase plane regions of different behavior.

The nature of the motion of the mass is determined by which type of trajectory its initial conditions determine. The simple closed trajectories encircling (0, 0) in the region bounded by the separatrices correspond to energies in the range 0<E<4. $0 < E < 4 .$ These closed trajectories represent periodic oscillations of the mass back and forth around the equilibrium point x=0. $x = 0 .$

The unbounded trajectories lying in the regions above and below the separatrices correspond to values of E greater than 4. These represent motions in which the mass approaches x=0 $x = 0$ with sufficient energy that it continues on through the equilibrium point, never to return again (as indicated in Fig. 9.4.5).

FIGURE 9.4.4.

Position–velocity phase plane portrait for the soft mass-and-spring system with m=1,k=4, $m = 1, k = 4,$ and β=1>0. $β = 1 > 0.$ The separatrices are emphasized.

FIGURE 9.4.5.

Position and velocity solution curves for the soft mass-and-spring system with m=1,k=4,β=1>0, $m = 1, k = 4, β = 1 > 0,$ and energy E=8 $E = 8$ —sufficiently great that the mass approaches the origin from the left and continues on indefinitely to the right.

The unbounded trajectories opening to the right and left correspond to values of E less than 4. These represent motions in which the mass initially is headed toward the equilibrium point x=0, $x = 0,$ but with insufficient energy to reach it. At some point the mass reverses direction and heads back whence it came.

In Fig. 9.4.4 it appears that the critical point (0, 0) is a stable center, whereas the critical points (±2,0) $(\pm 2, 0)$ look like saddle points of the equivalent first-order system

x' = y, y' = - 4 x + x 3

$x ′ = y, y ′ = - 4 x + x^{3}$ (11)

with Jacobian matrix

J (x, y) = [0 - 4 + 3 x 2 10] .

$J (x, y) = [\begin{array}{c} 0 & 1 \\ - 4 + 3 x^{2} & 0 \end{array}] .$

To check these observations against the usual critical-point analysis, we note first that the Jacobian matrix

J (0, 0) = [0 - 4 10]

$J (0, 0) = [\begin{array}{r} 0 & 1 \\ - 4 & 0 \end{array}]$

at the critical point (0, 0) has characteristic equation λ2+4=0 $λ^{2} + 4 = 0$ and pure imaginary eigenvalues λ1, λ2=±2i $λ_{1}, λ_{2} = \pm 2 i$ consistent with a stable center. Moreover, the Jacobian matrix

J (\pm 2, 0) = [0810]

$J (\pm 2, 0) = [\begin{array}{l} 0 & 1 \\ 8 & 0 \end{array}]$

corresponding to the other two critical points has characteristic equation λ2−8=0 $λ^{2} - 8 = 0$ and real eigenvalues λ1, λ2=±8–√ $λ_{1}, λ_{2} = \pm \sqrt{8}$ of opposite sign, consistent with the saddle-point behavior that we observe near (−2,0) $(- 2, 0)$ and (+2,0) $(+ 2, 0)$ .

Remark

Figures 9.4.2 and 9.4.4 illustrate a significant qualitative difference between hard springs with β<0 $β < 0$ and soft springs with β>0 $β > 0$ in the nonlinear equation mx''=kx+βx3. $m x ″ = k x + β x^{3} .$ Whereas the phase plane trajectories for a hard spring are all bounded, a soft spring has unbounded phase plane trajectories (as well as bounded ones). However, we should realize that the unbounded soft-spring trajectories cease to represent physically realistic motions faithfully when they exceed the spring’s capability of expansion without breaking.

Damped Nonlinear Vibrations

Suppose now that the mass on a spring is connected also to a dashpot that provides a force of resistance proportional to the velocity y=dx/dt $y = d x / d t$ of the mass. If the spring is still assumed nonlinear as in Eq. (2), then the equation of motion of the mass is

m x'' = - c x' - k x + β x 3,

$m x ″ = - c x ′ - k x + β x^{3},$ (12)

where c>0 $c > 0$ is the resistance constant. If β>0, $β > 0,$ then the equivalent first-order system

d x d t = y, d y d t = - k x - c y + β x 3 m = - c m y - k m x (1 - β k x 2)

$\frac{d x}{d t} = y, \frac{d y}{d t} = \frac{- k x - c y + β x^{3}}{m} = - \frac{c}{m} y - \frac{k}{m} x (1 - \frac{β}{k} x^{2})$ (13)

has critical points (0, 0) and (±k/β−−−√,0) $(\pm \sqrt{k / β}, 0)$ and Jacobian matrix

J (x, y) = ⎡ ⎣ 0 - k m + 3 β m x 2 1 - c m ⎤ ⎦ .

$J (x, y) = [\begin{array}{c} 0 & 1 \\ - \frac{k}{m} + \frac{3 β}{m} x^{2} & - \frac{c}{m} \end{array}] .$

Now the critical point at the origin is the most interesting one. The Jacobian matrix

J (0, 0) = [0 - k m 1 - c m]

$J (0, 0) = [\begin{array}{c} 0 & 1 \\ - \frac{k}{m} & - \frac{c}{m} \end{array}]$

has characteristic equation

(- λ) (- c m - λ) + k m = 1 m (m λ 2 + c λ + k) = 0

$(- λ) (- \frac{c}{m} - λ) + \frac{k}{m} = \frac{1}{m} (m λ^{2} + c λ + k) = 0$

and eigenvalues

λ 1, λ 2 = - c \pm c 2 - 4 k m - - - - - - - - \sqrt 2 m .

$λ_{1}, λ_{2} = \frac{- c \pm \sqrt{c^{2} - 4 k m}}{2 m} .$

It follows from Theorem 2 in Section 9.2 in that the critical point (0, 0) of the system in (13) is

a nodal sink if the resistance is so great that c2>4km $c^{2} > 4 k m$ (in which case the eigenvalues are negative and unequal), but is
a spiral sink if c2<4km $c^{2} < 4 k m$ (in which case the eigenvalues are complex conjugates with negative real part).

The following example illustrates the latter case. (In the borderline case with equal negative eigenvalues, the origin may be either a nodal or a spiral sink.)

Example 2

Damped soft spring Suppose that m=1, c=2, k=5, $m = 1, c = 2, k = 5,$ and β=54. $β = \frac{5}{4} .$ Then the nonlinear system in (13) is

d x d t = y, d y d t = - 5 x - 2 y + 5 4 x 3 = - 2 y - 5 x (1 - 1 4 x 2) .

$\frac{d x}{d t} = y, \frac{d y}{d t} = - 5 x - 2 y + \frac{5}{4} x^{3} = - 2 y - 5 x (1 - \frac{1}{4} x^{2}) .$ (14)

It has critical points (0,0), (±2,0) $(0, 0), (\pm 2, 0)$ and Jacobian matrix

J (x, y) = [0 - 5 + 15 4 x 2 1 - 2] .

$J (x, y) = [\begin{array}{c} 0 & 1 \\ - 5 + \frac{15}{4} x^{2} & - 2 \end{array}] .$

At (0, 0): The Jacobian matrix

J (0, 0) = [0 - 5 1 - 2]

$J (0, 0) = [\begin{array}{r} 0 & 1 \\ - 5 & - 2 \end{array}]$

has characteristic equation λ2+2λ+5=0 $λ^{2} + 2 λ + 5 = 0$ and has complex conjugate eigenvalues λ1, λ2=−1±2i $λ_{1}, λ_{2} = - 1 \pm 2 i$ with negative real part. Hence (0, 0) is a spiral sink of the nonlinear system in (14), and the linearized position function of the mass is of the form

x (t) = e - t (A cos 2 t + B sin 2 t)

$x (t) = e^{- t} (A \cos 2 t + B \sin 2 t)$

that corresponds to an exponentially damped oscillation about the equilibrium position x=0 $x = 0$ .

At (±2,0) $(\pm 2, 0)$ : The Jacobian matrix

J (\pm 2, 0) = [010 1 - 2]

$J (\pm 2, 0) = [\begin{array}{r} 0 & 1 \\ 10 & - 2 \end{array}]$

has characteristic equation λ2+2λ−10=0 $λ^{2} + 2 λ - 10 = 0$ and real eigenvalues λ1=−1−11−−√<0 $λ_{1} = - 1 - \sqrt{11} < 0$ and λ2=−1+11−−√>0 $λ_{2} = - 1 + \sqrt{11} > 0$ with different signs. It follows that (−2,0) $(- 2, 0)$ and (+2,0) $(+ 2, 0)$ are both saddle points of the system in (14).

The position–velocity phase plane portrait in Fig. 9.4.6 shows trajectories of (14) and the spiral sink at (0, 0), as well as the unstable saddle points at (−2,0) $(- 2, 0)$ and (2, 0). The emphasized separatrices divide the phase plane into regions of different behavior. The behavior of the mass depends on the region in which its initial point (x0,y0) $(x_{0}, y_{0})$ is located. If this initial point lies in

Region I between the separatrices, then the trajectory spirals into the origin as t→+∞, $t \to + \infty,$ and hence the periodic oscillations of the undamped case (Fig. 9.4.4) are now replaced with damped oscillations around the stable equilibrium position x=0 $x = 0$ ;
Region II, then the mass passes through x=0 $x = 0$ moving from left to right (x increasing);
Region III, then the mass passes through x=0 $x = 0$ moving from right to left (x decreasing);
Region IV, then the mass approaches (but does not reach) the unstable equilibrium position x=−2 $x = - 2$ from the left, but stops and then returns to the left;
Region V, then the mass approaches (but does not reach) the unstable equilibrium position x=2 $x = 2$ from the right, but stops and then returns to the right.

FIGURE 9.4.6.

Position–velocity phase plane portrait for the soft mass-and-spring system with m=1,k=5,β=54, $m = 1, k = 5, β = \frac{5}{4},$ and resistance constant c=2. $c = 2.$ The (black) separatrices are emphasized.

If the initial point (x0,y0) $(x_{0}, y_{0})$ lies precisely on one of the separatrices, then the corresponding trajectory either approaches the stable spiral point or recedes to infinity from a saddle point as t→+∞ $t \to + \infty$ .

The Nonlinear Pendulum

In Section 5.4 we derived the equation

d 2 θ d t 2 + g L sin θ = 0

$\frac{d^{2} θ}{d t^{2}} + \frac{g}{L} \sin θ = 0$ (15)

for the undamped oscillations of the simple pendulum shown in Fig. 9.4.7. There we used the approximation sin θ≈θ $\sin θ \approx θ$ for θ $θ$ near zero to replace Eq. (15) with the linear model

d 2 θ d t 2 + ω 2 θ = 0,

$\frac{d^{2} θ}{d t^{2}} + ω^{2} θ = 0,$ (16)

where ω2=g/L. $ω^{2} = g / L .$ The general solution

θ (t) = A cos ω t + B sin ω t

$θ (t) = A \cos ω t + B \sin ω t$ (17)

of Eq. (16) describes oscillations around the equilibrium position θ=0 $θ = 0$ with circular frequency ω $ω$ and amplitude C=(A2+B2)1/2 $C = {(A^{2} + B^{2})}^{1/2}$ .

The linear model does not adequately describe the possible motions of the pendulum for large values of θ. $θ .$ For instance, the equilibrium solution θ(t)≡π $θ (t) \equiv π$ of Eq. (15), with the pendulum standing straight up, does not satisfy the linear equation in (16). Nor does Eq. (17) include the situation in which the pendulum “goes over the top” repeatedly, so that θ(t) $θ (t)$ is a steadily increasing rather than an oscillatory function of t. To investigate these phenomena we must analyze the nonlinear equation θ''+ω2 sin θ=0 $θ ″ + ω^{2} \sin θ = 0$ rather than merely its linearization θ''+ω2θ=0. $θ ″ + ω^{2} θ = 0 .$ We also want to include the possibility of resistance proportional to velocity, so we consider the general nonlinear pendulum equation

d 2 θ d t 2 + c d θ d t + ω 2 sin θ = 0.

$\frac{d^{2} θ}{d t^{2}} + c \frac{d θ}{d t} + ω^{2} \sin θ = 0.$ (18)

The case c>0 $c > 0$ corresponds to damped motion in which there actually is resistance proportional to (angular) velocity. But we examine first the undamped case in which c=0. $c = 0 .$ With x(t)=θ(t) $x (t) = θ (t)$ and y(t)=θ'(t) $y (t) = θ ′ (t)$ the equivalent first-order system is

d x d t = y, d y d t = - ω 2 sin x .

$\frac{d x}{d t} = y, \frac{d y}{d t} = - ω^{2} \sin x .$ (19)

We see that this system is almost linear by writing it in the form

d x d t = y, d y d t = - ω 2 x + g (x),

$\begin{array}{l} \frac{d x}{d t} = y, \\ \frac{d y}{d t} = - ω^{2} x + g (x), \end{array}$ (20)

where

g (x) = - ω 2 (sin x - x) = ω 2 (x 3 3 ! - x 5 5 ! + \dots)

$g (x) = - ω^{2} (\sin x - x) = ω^{2} (\frac{x^{3}}{3!} - \frac{x^{5}}{5!} + \dots)$

has only higher-degree terms.

The critical points of the system in (19) are the points (nπ,0) $(n π, 0)$ with n an integer, and its Jacobian matrix is given by

J (x, y) = [0 - ω 2 cos x 10] .

$J (x, y) = [\begin{array}{c} 0 & 1 \\ - ω^{2} \cos x & 0 \end{array}] .$ (21)

The nature of the critical point (nπ,0) $(n π, 0)$ depends on whether n is even or odd.

Even Case: If n=2m $n = 2 m$ is an even integer, then cos nπ=+1, $\cos n π = + 1,$ so (21) yields the matrix

J (2 m π, 0) = [0 - ω 2 10]

$J (2 m π, 0) = [\begin{array}{c} 0 & 1 \\ - ω^{2} & 0 \end{array}]$

with characteristic equation λ2+ω2=0 $λ^{2} + ω^{2} = 0$ and pure imaginary eigenvalues λ1, λ2=±ωi. $λ_{1}, λ_{2} = \pm ω i .$ The linearization of (19) at (nπ,0) $(n π, 0)$ is therefore the system

d u d t = v, d v d t = - ω 2 u

$\frac{d u}{d t} = v, \frac{d v}{d t} = - ω^{2} u$ (22)

for which (0, 0) is the familiar stable center enclosed by elliptical trajectories (as in Example 3 of Section 9.1). Although this is the delicate case for which Theorem 2 of Section 9.2 does not settle the matter, we will see presently that (2mπ,0) $(2 m π, 0)$ is also a stable center for the original nonlinear pendulum system in (19).

Odd Case: If n=2m+1 $n = 2 m + 1$ is an odd integer, then cos nπ=−1, $\cos n π = - 1,$ so (21) yields the matrix

J ((2 m + 1) π, 0) = [0 ω 2 10]

$J ((2 m + 1) π, 0) = [\begin{array}{c} 0 & 1 \\ ω^{2} & 0 \end{array}]$

with characteristic equation λ2−ω2=0 $λ^{2} - ω^{2} = 0$ and real eigenvalues λ1, λ2=±ω $λ_{1}, λ_{2} = \pm ω$ with different signs. The linearization of (19) at ((2m+1)π,0) $((2 m + 1) π, 0)$ is therefore the system

d u d t = v, d v d t = ω 2 u

$\frac{d u}{d t} = v, \frac{d v}{d t} = ω^{2} u$ (23)

for which (0, 0) is a saddle point. It follows from Theorem 2 of Section 9.2 that the critical point ((2m+1)π,0) $((2 m + 1) π, 0)$ is a similar saddle point for the original nonlinear pendulum system in (19).

The Trajectories: We can see how these “even centers” and “odd saddle points” fit together by solving the system in (19) explicitly for the phase plane trajectories. If we write

d y d x = d y / d t d x / d t = - ω 2 sin x y

$\frac{d y}{d x} = \frac{d y / d t}{d x / d t} = - \frac{ω^{2} \sin x}{y}$

and separate the variables,

y d y + ω 2 sin x d x = 0,

$y d y + ω^{2} \sin x d x = 0,$

then integration from x=0 $x = 0$ to x=x $x = x$ yields

1 2 y 2 + ω 2 (1 - cos x) = E .

$\frac{1}{2} y^{2} + ω^{2} (1 - \cos x) = E .$ (24)

We write E for the arbitrary constant of integration because, if physical units are so chosen that m=L=1, $m = L = 1,$ then the first term on the left is the kinetic energy and the second term the potential energy of the mass on the end of the pendulum. Then E is the total mechanical energy; Eq. (24) thus expresses conservation of mechanical energy for the undamped pendulum.

If we solve Eq. (24) for y and use a half-angle identity, we get the equation

y = \pm 2 E - 4 ω 2 sin 2 1 2 x - - - - - - - - - - - - - \sqrt

$y = \pm \sqrt{2 E - 4 ω^{2} \sin^{2} \frac{1}{2} x}$ (25)

that defines the phase plane trajectories. Note that the radicand in (25) remains positive if E>2ω2. $E > 2 ω^{2} .$ Figure 9.4.8 shows (along with a direction field) the results of plotting these trajectories for various values of the energy E.

FIGURE 9.4.8.

Position–velocity phase plane portrait for the undamped pendulum system x'=y,y'=−sinx. $x ′ = y, y ′ = - \sin x .$ The (black) separatrices are emphasized.

The emphasized separatrices in Fig. 9.4.8 correspond to the critical value E=2ω2 $E = 2 ω^{2}$ of the energy; they enter and leave the unstable critical points (nπ,0) $(n π, 0)$ with n an odd integer. Following the arrows along a separatrix, the pendulum theoretically approaches a balanced vertical position θ=x=(2m+1)π $θ = x = (2 m + 1) π$ with just enough energy to reach it but not enough to “go over the top.” The instability of this equilibrium position indicates that this behavior may never be observed in practice!

The simple closed trajectories encircling the stable critical points—all of which correspond to the downward position θ=2mπ $θ = 2 m π$ of the pendulum—represent periodic oscillations of the pendulum back and forth around the stable equilibrium position θ=0. $θ = 0 .$ These correspond to energies E<2ω2 $E < 2 ω^{2}$ that are insufficient for the pendulum to ascend to the vertical upward position—so its back-and-forth motion is that which we normally associate with a “swinging pendulum.”

The unbounded trajectories with E>2ω2 $E > 2 ω^{2}$ represent whirling motions of the pendulum in which it goes over the top repeatedly—in a clockwise direction if y(t) remains positive, in a counterclockwise direction if y(t) is negative.

Period of Undamped Oscillation

If the pendulum is released from rest with initial conditions

x (0) = θ (0) = α, y (0) = θ' (0) = 0,

$x (0) = θ (0) = α, y (0) = θ ′ (0) = 0,$ (26)

then Eq. (24) with t=0 $t = 0$ reduces to

ω 2 (1 - cos α) = E .

$ω^{2} (1 - \cos α) = E .$ (27)

Hence E<2ω2 $E < 2 ω^{2}$ if 0<α<π, $0 < α < π,$ so a periodic oscillation of the pendulum ensues. To determine the period of this oscillation, we subtract Eq. (27) from Eq. (24) and write the result (with x=θ $x = θ$ and y=dθ/dt $y = d θ / d t$ ) in the form

1 2 (d θ d t) 2 = ω 2 (cos θ - cos α) .

$\frac{1}{2} {(\frac{d θ}{d t})}^{2} = ω^{2} (\cos θ - \cos α) .$ (28)

The period T of time required for one complete oscillation is four times the amount of time required for θ $θ$ to decrease from θ=α $θ = α$ to θ=0, $θ = 0,$ one-fourth of an oscillation. Hence we solve Eq. (28) for dt/dθ $d t / d θ$ and integrate to get

T = 4 ω 2 - \sqrt \int α 0 d θ cos θ - cos α - - - - - - - - - - \sqrt .

$T = \frac{4}{ω \sqrt{2}} \int_{0}^{α} \frac{d θ}{\sqrt{\cos θ - \cos α}} .$ (29)

To attempt to evaluate this integral we first use the identity cos θ=1−2sin2(θ/2) $\cos θ = 1 - 2 \sin^{2} (θ / 2)$ and get

T = 2 ω \int α 0 d θ k 2 - sin 2 ( θ / 2 ) - - - - - - - - - - - \sqrt,

$T = \frac{2}{ω} \int_{0}^{α} \frac{d θ}{\sqrt{k^{2} - \sin^{2} (θ / 2)}},$

where

k = sin α 2 .

$k = \sin \frac{α}{2} .$

Next, the substitution u=(1/k)sin(θ/2) $u = (1 / k) \sin (θ / 2)$ yields

T = 4 ω \int 10 d u ( 1 - u 2 ) ( 1 - k 2 u 2 ) - - - - - - - - - - - - - - - \sqrt .

$T = \frac{4}{ω} \int_{0}^{1} \frac{d u}{\sqrt{(1 - u^{2}) (1 - k^{2} u^{2})}} .$

Finally, the substitution u=sin ϕ $u = \sin ϕ$ gives

T = 4 ω \int π / 2 0 d ϕ 1 - k 2 sin 2 ϕ - - - - - - - - - \sqrt .

$T = \frac{4}{ω} \int_{0}^{π / 2} \frac{d ϕ}{\sqrt{1 - k^{2} \sin^{2} ϕ}} .$ (30)

The integral in (30) is the elliptic integral of the first kind that is often denoted by F(k,π/2). $F (k, π / 2) .$ Whereas elliptic integrals normally cannot be evaluated in closed form, this integral can be approximated numerically as follows. First we use the binomial series

1 1 - x - - - - - \sqrt = 1 + \sum n = 1 \infty 1 \cdot 3 \dots ( 2 n - 1 ) 2 \cdot 4 \dots ( 2 n ) x n

$\frac{1}{\sqrt{1 - x}} = 1 + \sum_{n = 1}^{\infty} \frac{1 \cdot 3 \dots (2 n - 1)}{2 \cdot 4 \dots (2 n)} x^{n}$ (31)

with x=k2 sin2 ϕ<1 $x = k^{2} \sin^{2} ϕ < 1$ to expand the integrand in (30). Then we integrate termwise using the tabulated integral formula

\int π / 2 0 sin 2 n ϕ d ϕ = π 2 \cdot 1 \cdot 3 \dots ( 2 n - 1 ) 2 \cdot 4 \dots ( 2 n ) .

$\int_{0}^{π / 2} \sin^{2 n} ϕ d ϕ = \frac{π}{2} \cdot \frac{1 \cdot 3 \dots (2 n - 1)}{2 \cdot 4 \dots (2 n)} .$ (32)

The final result is the formula

T = = 2 π ω [1 + \sum n = 1 \infty (1 \cdot 3 \dots ( 2 n - 1 ) 2 \cdot 4 \dots ( 2 n )) 2 k 2 n] T 0 [1 + (1 2) 2 k 2 + (1 \cdot 3 2 \cdot 4) 2 k 4 + (1 \cdot 3 \cdot 5 2 \cdot 4 \cdot 6) 2 k 6 + \dots]

$\begin{array}{rcl} T & = & \frac{2 π}{ω} [1 + \sum_{n = 1}^{\infty} {(\frac{1 \cdot 3 \dots (2 n - 1)}{2 \cdot 4 \dots (2 n)})}^{2} k^{2 n}] \\ = & T_{0} [1 + {(\frac{1}{2})}^{2} k^{2} + {(\frac{1 \cdot 3}{2 \cdot 4})}^{2} k^{4} + {(\frac{1 \cdot 3 \cdot 5}{2 \cdot 4 \cdot 6})}^{2} k^{6} + \dots] \end{array}$ (33)

for the period T of the nonlinear pendulum released from rest with initial angle θ(0)=α, $θ (0) = α,$ in terms of the linearized period T0=2π/ω $T_{0} = 2 π / ω$ and k=sin(α/2) $k = \sin (α / 2)$ .

The infinite series within the second pair of brackets in Eq. (33) gives the factor T/T0 $T / T_{0}$ by which the nonlinear period T is longer than the linearized period. The table in Fig. 9.4.9, obtained by summing this series numerically, shows how T/T0 $T / T_{0}$ increases as α $α$ is increased. Thus T is 0.19% greater than T0 $T_{0}$ if α=10°, $α = 10 °,$ whereas T is 18.03% greater than T0 $T_{0}$ if α=90°. $α = 90 ° .$ But even a 0.19% discrepancy is significant—the calculation

(0.0019) \times 3600 seconds hour \times 24 hours day \times 7 days week \approx 1149 (seconds / week)

$(0.0019) \times 3600 \frac{seconds}{hour} \times 24 \frac{hours}{day} \times 7 \frac{days}{week} \approx 1149 (seconds / week)$

shows that the linearized model is quite inadequate for a pendulum clock; a discrepancy of 19 min 9 s after only one week is unacceptable.

FIGURE 9.4.9.

Dependence of the period T of a nonlinear pendulum on its initial angle α $α$ .

α $α$	T/T0 $T / T_{0}$
10° $10 °$	1.0019
20° $20 °$	1.0077
30° $30 °$	1.0174
40° $40 °$	1.0313
50° $50 °$	1.0498
60° $60 °$	1.0732
70° $70 °$	1.1021
80° $80 °$	1.1375
90° $90 °$	1.1803

Damped Pendulum Oscillations

Finally, we discuss briefly the damped nonlinear pendulum. The almost linear first-order system equivalent to Eq. (19) is

d x d t = y, d y d t = - ω 2 sin x - c y,

$\begin{array}{l} \frac{d x}{d t} = y, \\ \frac{d y}{d t} = - ω^{2} \sin x - c y, \end{array}$ (34)

and again the critical points are of the form (nπ,0) $(n π, 0)$ where n is an integer. In Problems 9 through 11 we ask you to verify that

If n is odd, then (nπ,0) $(n π, 0)$ is an unstable saddle point of (34), just as in the undamped case; but
If n is even and c2>4ω2, $c^{2} > 4 ω^{2},$ then (nπ,0) $(n π, 0)$ is a nodal sink; whereas
If n is even and c2<4ω2, $c^{2} < 4 ω^{2},$ then (nπ,0) $(n π, 0)$ is a spiral sink.

Figure 9.4.10 illustrates the phase plane trajectories for the more interesting underdamped case, c2<4ω2. $c^{2} < 4 ω^{2} .$ Other than the physically unattainable separatrix trajectories that enter unstable saddle points, every trajectory eventually is “trapped” by one of the stable spiral points (nπ,0) $(n π, 0)$ with n an even integer. What this means is that even if the pendulum starts with enough energy to go over the top, after a certain (finite) number of revolutions it has lost enough energy that thereafter it undergoes damped oscillations around its stable (lower) equilibrium position.

FIGURE 9.4.10.

Position–velocity phase plane portrait for the damped pendulum system x'=y,y'=−sinx−14y. $x ′ = y, y ′ = - \sin x - \frac{1}{4} y .$ The (black) separatrices are emphasized.

9.4 Problems

In Problems 1 through 4, show that the given system is almost linear with (0, 0) as a critical point, and classify this critical point as to type and stability. Use a computer system or graphing calculator to construct a phase plane portrait that illustrates your conclusion.

dxdt=1−ex+2y, dydt=−x−4sin y $\frac{d x}{d t} = 1 - e^{x} + 2 y, \frac{d y}{d t} = - x - 4 \sin y$
dxdt=2sin x+sin y, dydt=sin x+2sin y $\frac{d x}{d t} = 2 \sin x + \sin y, \frac{d y}{d t} = \sin x + 2 \sin y$ (Fig. 9.4.11)

FIGURE 9.4.11.

Trajectories of the system in Problem 2.
dxdt=ex+2y−1, dydt=8x+ey−1 $\frac{d x}{d t} = e^{x} + 2 y - 1, \frac{d y}{d t} = 8 x + e^{y} - 1$
dxdt=sin xcos y−2y, dydt=4x−3cos xsin y $\frac{d x}{d t} = \sin x \cos y - 2 y, \frac{d y}{d t} = 4 x - 3 \cos x \sin y$

Find and classify each of the critical points of the almost linear systems in Problems 5 through 8. Use a computer system or graphing calculator to construct a phase plane portrait that illustrates your findings.

dxdt=−x+sin y, dydt=2x $\frac{d x}{d t} = - x + \sin y, \frac{d y}{d t} = 2 x$
dxdt=y, dydt=sin πx−y $\frac{d x}{d t} = y, \frac{d y}{d t} = \sin π x - y$
dxdt=1−ex−y, dydt=2sin x $\frac{d x}{d t} = 1 - e^{x - y}, \frac{d y}{d t} = 2 \sin x$
dxdt=3sin x+y, dydt=sin x+2y $\frac{d x}{d t} = 3 \sin x + y, \frac{d y}{d t} = \sin x + 2 y$

Critical Points for Damped Pendulum

Problems 9 through 11 deal with the damped pendulum system x'=y, y'=−ω2 sin x−cy $x ′ = y, y ′ = - ω^{2} \sin x - c y$ .

Show that if n is an odd integer, then the critical point (nπ,0) $(n π, 0)$ is a saddle point for the damped pendulum system.
Show that if n is an even integer and c2>4ω2, $c^{2} > 4 ω^{2},$ then the critical point (nπ,0) $(n π, 0)$ is a nodal sink for the damped pendulum system.
Show that if n is an even integer and c2<4ω2, $c^{2} < 4 ω^{2},$ then the critical point (nπ,0) $(n π, 0)$ is a spiral sink for the damped pendulum system.

Critical Points for Mass-Spring System

In each of Problems 12 through 16, a second-order equation of the form x''+f(x,x')=0, $x ″ + f (x, x ′) = 0,$ corresponding to a certain mass-and-spring system, is given. Find and classify the critical points of the equivalent first-order system.

x''+20x−5x3=0 $x ″ + 20 x - 5 x^{3} = 0$ : Verify that the critical points resemble those shown in Fig. 9.4.4.
x''+2x'+20x−5x3=0 $x ″ + 2 x ′ + 20 x - 5 x^{3} = 0$ : Verify that the critical points resemble those shown in Fig. 9.4.6.
x''−8x+2x3=0 $x ″ - 8 x + 2 x^{3} = 0$ : Here the linear part of the force is repulsive rather than attractive (as for an ordinary spring). Verify that the critical points resemble those shown in Fig. 9.4.12. Thus there are two stable equilibrium points and three types of periodic oscillations.
x''+4x−x2=0 $x ″ + 4 x - x^{2} = 0$ : Here the force function is nonsymmetric. Verify that the critical points resemble those shown in Fig. 9.4.13.
x''+4x−5x3+x5=0 $x ″ + 4 x - 5 x^{3} + x^{5} = 0$ : The idea here is that terms through the fifth degree in an odd force function have been retained. Verify that the critical points resemble those shown in Fig. 9.4.14.

Critical Points for Physical Systems

In Problems 17 through 20, analyze the critical points of the indicated system, use a computer system to construct an illustrative position–velocity phase plane portrait, and describe the oscillations that occur.

Example 2 in this section illustrates the case of damped vibrations of a soft mass-spring system. Investigate an example of damped vibrations of a hard mass–spring system by using the same parameters as in Example 2, except now with β=−54<0 $β = - \frac{5}{4} < 0$ .
Example 2 illustrates the case of damped vibrations of a soft mass–spring system with the resistance proportional to the velocity. Investigate an example of resistance proportional to the square of the velocity by using the same parameters as in Example 2, but with resistance term −cx'|x'| $- c x ′ | x ′ |$ instead of −cx' $- c x ′$ in Eq. (12).
Now repeat Example 2 with both the alterations corresponding to Problems 17 and 18. That is, take β=−54<0 $β = - \frac{5}{4} < 0$ and replace the resistance term in Eq. (12) with −cx'|x'| $- c x ′ | x ′ |$ .
The equations x'=y, y'=−sin x−14y∣∣y∣∣ $x ′ = y, y ′ = - \sin x - \frac{1}{4} y | y |$ model a damped pendulum system as in Eqs. (34) and Fig. 9.4.10. But now the resistance is proportional to the square of the angular velocity of the pendulum. Compare the oscillations with those that occur when the resistance is proportional to the angular velocity itself.

Period of Oscillation

Problems 21 through 26 outline an investigation of the period T of oscillation of a mass on a nonlinear spring with equation of motion

d 2 x d t 2 + ϕ (x) = 0.

$\frac{d^{2} x}{d t^{2}} + ϕ (x) = 0.$ (35)

If ϕ(x)=kx $ϕ (x) = k x$ with k>0, $k > 0,$ then the spring actually is linear with period T0=2π/k−−√ $T_{0} = 2 π / \sqrt{k}$ .

FIGURE 9.4.12.

The phase portrait for Problem 14.

FIGURE 9.4.13.

The phase portrait for Problem 15.

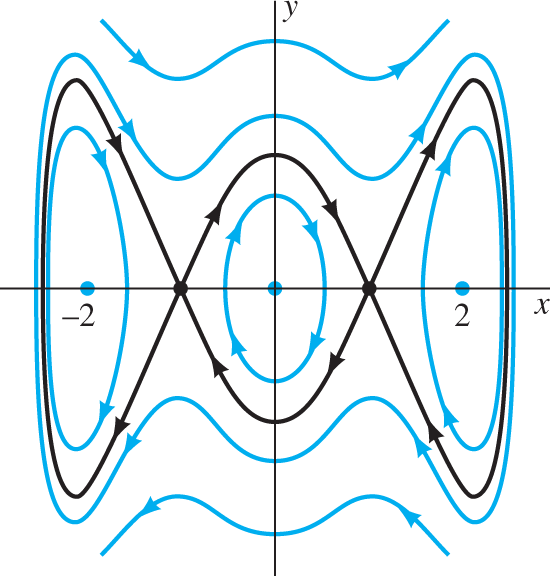
FIGURE 9.4.14.

The phase portrait for Problem 16.

Integrate once (as in Eq. (6)) to derive the energy equation

$1 2 y 2 + V (x) = E,$ $\frac{1}{2} y^{2} + V (x) = E,$ (36)

where y=dx/dt $y = d x / d t$ and

$V (x) = \int x 0 ϕ (u) d u .$ $V (x) = \int_{0}^{x} ϕ (u) d u .$ (37)
If the mass is released from rest with initial conditions x(0)=x0, y(0)=0 $x (0) = x_{0}, y (0) = 0$ and periodic oscillations ensue, conclude from Eq. (36) that E=V(x0) $E = V (x_{0})$ and that the time T required for one complete oscillation is

$T = 4 2 - \sqrt \int x 0 0 d u V ( x 0 ) - V ( u ) - - - - - - - - - - - \sqrt .$ $T = \frac{4}{\sqrt{2}} \int_{0}^{x_{0}} \frac{d u}{\sqrt{V (x_{0}) - V (u)}} .$ (38)
If ϕ(x)=kx−βx3 $ϕ (x) = k x - β x^{3}$ as in the text, deduce from Eqs. (37) and (38) that

$T = 4 2 - \sqrt \int x 0 0 d x ( x 2 0 - u 2 ) ( 2 k - β x 2 0 - β u 2 ) - - - - - - - - - - - - - - - - - - - - - \sqrt .$ $T = 4 \sqrt{2} \int_{0}^{x_{0}} \frac{d x}{\sqrt{(x_{0}^{2} - u^{2}) (2 k - β x_{0}^{2} - β u^{2})}} .$ (39)
Substitute u=x0cos ϕ $u = x_{0} \cos ϕ$ in (39) to show that

$T = 2 T 0 π 1 - ϵ - - - - \sqrt \int π / 2 0 d ϕ 1 - μ sin 2 ϕ - - - - - - - - - \sqrt,$ $T = \frac{2 T_{0}}{π \sqrt{1 - ϵ}} \int_{0}^{π / 2} \frac{d ϕ}{\sqrt{1 - μ \sin^{2} ϕ}},$ (40)

where T0=2π/k−−√ $T_{0} = 2 π / \sqrt{k}$ is the linear period,

$ϵ = β k x 20, and μ = - 1 2 \cdot ϵ 1 - ϵ .$ $ϵ = \frac{β}{k} x_{0}^{2}, and μ = - \frac{1}{2} \cdot \frac{ϵ}{1 - ϵ} .$ (41)
Finally, use the binomial series in (31) and the integral formula in (32) to evaluate the elliptic integral in (40) and thereby show that the period T of oscillation is given by

$T = T 0 1 - ϵ - - - - \sqrt (1 + 1 4 μ + 9 64 μ 2 + 25 256 μ 3 + \dots) .$ $T = \frac{T_{0}}{\sqrt{1 - ϵ}} (1 + \frac{1}{4} μ + \frac{9}{64} μ^{2} + \frac{25}{256} μ^{3} + \dots) .$ (42)
If ϵ=βx20/k $ϵ = β x_{0}^{2} / k$ is sufficiently small that ϵ2 $ϵ^{2}$ is negligible, deduce from Eqs. (41) and (42) that

$T \approx T 0 (1 + 3 8 ϵ) = T 0 (1 + 3 β 8 k x 20) .$ $T \approx T_{0} (1 + \frac{3}{8} ϵ) = T_{0} (1 + \frac{3 β}{8 k} x_{0}^{2}) .$ (43)

It follows that
- If β>0, $β > 0,$ so the spring is soft, then T>T0, $T > T_{0},$ and increasing x0 $x_{0}$ increases T, so the larger ovals in Fig. 9.4.4 correspond to smaller frequencies.
- If β<0, $β < 0,$ so the spring is hard, then T<T0, $T < T_{0},$ and increasing x0 $x_{0}$ decreases T, so the larger ovals in Fig. 9.4.2 correspond to larger frequencies.

9.4 Application The Rayleigh, van der Pol, and FitzHugh-Nagumo Equations

Here we present a trio of nonlinear differential equations or systems of equations, drawn from the areas of acoustics, electrical engineering, and neuroscience. Each of these models has been fundamental within its field; taken together, they give some indication of the importance of nonlinear equations across a wide variety of applications.

Rayleigh’s Equation

The British mathematical physicist Lord Rayleigh (John William Strutt, 1842–1919) introduced an equation of the form

m x'' + k x = a x' - b (x') 3

$m x ″ + k x = a x ′ - b {(x ′)}^{3}$ (1)

to model the oscillations of a clarinet reed. With y=x' $y = x ′$ we get the autonomous system

x' = y, y' = - k x + a y - b y 3 m,

$\begin{array}{l} x ′ = y, \\ y ′ = \frac{- k x + a y - b y^{3}}{m}, \end{array}$ (2)

whose phase plane portrait is shown in Fig. 9.4.15 (for the case m=k=a=b=1 $m = k = a = b = 1$ ). The outward and inward spiral trajectories converge to a “limit cycle” solution that corresponds to periodic oscillations of the reed. The period T (and hence the frequency) of these oscillations can be measured on a tx $t x$ -solution curve plotted as in Fig. 9.4.16. This period of oscillation depends only on the parameters m, k, a, and b in Eq. (1) and is independent of the initial conditions (why?).

FIGURE 9.4.15.

Phase plane portrait for the Rayleigh system in (2) with m=k=a=b=1 $m = k = a = b = 1$ .

FIGURE 9.4.16.

The `tx`-solution curve with initial conditions x(0)=0.01,x'(0)=0 $x (0) = 0.01, x^{′} (0) = 0$ .

Choose your own parameters m, k, a, and b (perhaps the least four nonzero digits in your student ID number), and use an available ODE plotting utility to plot trajectories and solution curves as in Figs. 9.4.15 and 9.4.16. Change one of your parameters to see how the amplitude and frequency of the resulting periodic oscillations are altered.

Van der Pol’s Equation

Figure 9.4.17 shows a simple RLC circuit in which the usual (passive) resistance R has been replaced with an active element (such as a vacuum tube or semiconductor) across which the voltage drop V is given by a known function f(I) of the current I. Of course, V=f(I)=IR $V = f (I) = I R$ for a resistor. If we substitute f(I) for IR in the well-known RLC-circuit equation LI'+RI+Q/C=0, $L I ′ + R I + Q / C = 0,$ then differentiation gives the second-order equation

L I'' + f' (I) I' + I C = 0.

$L I ″ + f ′ (I) I ′ + \frac{I}{C} = 0.$ (3)

FIGURE 9.4.17.

A simple circuit with an active element.

In a 1924 study of oscillator circuits in early commercial radios, Balthasar van der Pol (1889–1959) assumed the voltage drop to be given by a nonlinear function of the form f(I)=bI3−aI, $f (I) = {b I}^{3} - a I,$ which with Eq. (3) becomes

L I'' + (3 b I 2 - a) I' + I C = 0.

$L I ″ + (3 b I^{2} - a) I ′ + \frac{I}{C} = 0.$ (4)

This equation is closely related to Rayleigh’s equation and has phase portraits resembling Fig. 9.4.15. Indeed, differentiation of the second equation in (2) and the resubstitution x'=y $x ′ = y$ yield the equation

m y'' + (3 b y 2 - a) y' + k y = 0,

$m y ″ + (3 b y^{2} - a) y ′ + k y = 0,$ (5)

which has the same form as Eq. (4).

If we denote by τ $τ$ the time variable in Eq. (4) and make the substitutions I=px, t=τ/LC−−−√, $I = p x, t = τ / \sqrt{L C},$ the result is

d 2 x d t 2 + (3 b p 2 x 2 - a) C L - - \sqrt d x d t + x = 0.

$\frac{d^{2} x}{d t^{2}} + (3 b p^{2} x^{2} - a) \sqrt{\frac{C}{L}} \frac{d x}{d t} + x = 0.$

With p=a/(3b)−−−−−√ $p = \sqrt{a / (3 b)}$ and μ=aC/L−−−−√, $μ = a \sqrt{C / L},$ this gives the standard form

x'' + μ (x 2 - 1) x' + x = 0

$x ″ + μ (x^{2} - 1) x ′ + x = 0$ (6)

of van der Pol’s equation.

For every nonnegative value of the parameter μ, $μ,$ the solution of van der Pol’s equation with x(0)=2, x'(0)=0 $x (0) = 2, x ′ (0) = 0$ is periodic, and the corresponding phase plane trajectory is a limit cycle to which the other trajectories converge (as in Fig. 9.4.15). It will be instructive for you to solve van der Pol’s equation numerically and to plot this periodic trajectory for a selection of values from μ=0 $μ = 0$ to μ=1000 $μ = 1000$ or more. With μ=0 $μ = 0$ it is a circle of radius 2 (why?). Figure 9.4.18 shows the periodic trajectory with μ=1, $μ = 1,$ and Fig. 9.4.19 shows the corresponding x(t) and y(t) solution curves. When μ $μ$ is large, van der Pol’s equation is quite “stiff” and the periodic trajectory is more eccentric as in Fig. 9.4.20, which was plotted using Matlab’s stiff ODE solver ode15s. The corresponding x(t) and y(t) solution curves in Figs. 9.4.21 and 9.4.22 reveal surprising behavior of these component functions. Each alternates long intervals of very slow change with periods of abrupt change during very short time intervals that correspond to the “quasi-discontinuities” that are visible in Figs. 9.4.21 and 9.4.22. For instance, Fig. 9.4.23 shows that, between t=1614.28 $t = 1614.28$ and t=1614.29, $t = 1614.29,$ the value of y(t) zooms from near zero to over 1300 and back again. Perhaps you can measure the distance between x- or y-intercepts to show that the period of circuit around the cycle in Fig. 9.4.20 is approximately T=1614. $T = 1614 .$ Indeed, this calculation and the construction of figures like those shown here may serve as a good test of the robustness of your computer system’s ODE solver.

FIGURE 9.4.19.

`x`(`t`) and `y`(`t`) solution curves defining the periodic solution of van der Pol’s equation with μ=1 $μ = 1$ .

FIGURE 9.4.20.

The phase plane trajectory of the periodic solution of van der Pol’s equation with μ=1000 $μ = 1000$ .

FIGURE 9.4.21.

Graph of `x`(`t`) with μ=1000 $μ = 1000$ .

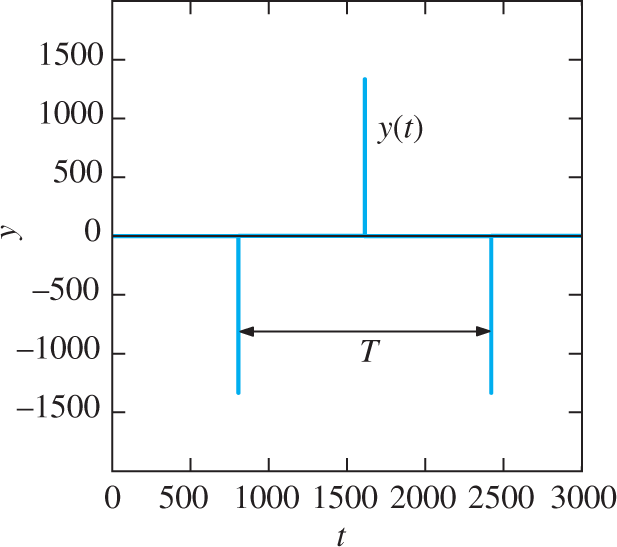
FIGURE 9.4.22.

Graph of `y`(`t`) with μ=1000 $μ = 1000$ .

FIGURE 9.4.23.

The upper spike in the graph of `y`(`t`).

You might also plot other trajectories for μ=10, 100 $μ = 10, 100$ or 1000 that (like the trajectories in Fig. 9.4.18) are “attracted” from within and without by the limit cycle. The origin looks like a spiral point in Fig 9.4.18. Indeed, show that (0, 0) is a spiral source for van der Pol’s equation if 0<μ<2 $0 < μ < 2$ but is a nodal source if μ≥2 $μ \geq 2$ .

The FitzHugh-Nagumo Equations

Since the early experiments of Luigi Galvani (1737–1798) in which electrical stimulus caused the leg muscles of dead frogs to twitch, the electrical properties of neurons, the cells that form the building blocks of the nervous system, have been intensively studied. One of the most important of those properties is the action potential, an electrical signal that travels from the body of a neuron down along its axon (Fig. 9.4.24). Action potentials are the units of information of the nervous system; when an action potential reaches the end of the axon, chemicals known as neurotransmitters are released from the axon terminals. These neurotransmitters then find receptors in the dendrites of other nerve cells, causing action potentials in those “target” neurons, and thus propagating the “message.” Because of the great speed with which action potentials traverse the neuron, they provide a mechanism by which signals can be rapidly transmitted through the nervous system.

Action potentials are particularly known for their all-or-none character. If the stimulus received by a target neuron is below a certain threshold, then no action potential is generated. If this threshold is exceeded, however, then the neuron will “fire” an action potential, or perhaps (if the stimulus is sufficiently strong) several action potentials in succession. In this way, the nervous system’s method of electrical signaling resembles the binary code used by computers.

FIGURE 9.4.24.

The structure of a typical neuron.

In the early 1950’s A. F. Huxley (1917–2012) and A. L. Hodgkin (1914–1998) published a landmark series of papers in which they modeled the action potential in the giant axon of the squid as an electrical circuit. The focus of this model was the neuron’s membrane potential, that is, the voltage difference between the inside and outside of the nerve cell. In its resting state, a typical neuron has a negative membrane potential, that is, the inside of the cell is at a lower voltage than the surrounding medium. (We now know that this voltage difference is largely due to “ion pumps” in the cell membrane, which maintain a lower concentration of positively charged sodium ions inside the cell than in the surrounding medium. These pumps require energy, and indeed a significant portion of the body’s metabolic energy is devoted to this task.) Potassium ions also play an important role in neuron electrical activity.

During an action potential, the membrane potential exhibits a characteristic pattern of sudden and rapid changes through positive and negative values as the electrical signal traverses the neuron. A central goal of Hodgkin and Huxley’s work was to explain these changes in terms of the sodium and potassium conductances of the neuron membrane. Conductance—the reciprocal of resistance—is a measure of the permeability of the membrane to charged ions. An increase in the sodium conductance, for example, allows sodium ions to flow more freely across the membrane, from areas of high concentration to low. Hodgkin and Huxley proposed that during an action potential, an electrical stimulus (arising from another neuron “upstream,” for example) causes changes in the neuron membrane’s sodium and potassium conductances. This results in a series of flows of charged ions, and thus electrical currents, across the cell membrane.

The researchers applied some of the basic principles of circuit theory to model these currents. The result was a system of four nonlinear differential equations, whose variables are the neuron membrane potential together with three other quantities related to the membrane’s sodium and potassium conductances. Not only did the predictions of this model show remarkable accord with experimental results, they also helped point the way to subsequent discoveries in neurophysiology. The Hodgkin-Huxley model was a triumph both of experimental technique and theoretical analysis, and remains today the starting point for mathematical modeling of action potentials. Together with John Eccles, Hodgkin and Huxley were awarded the 1963 Nobel Prize in Physiology or Medicine for their work.

Analysis of the Hodgkin-Huxley model can be challenging, however, because its phase space is four-dimensional, making features such as solution curves difficult to visualize. For this reason, in 1961 Richard FitzHugh (1922–2007) proposed a two-dimensional simplification of the Hodgkin-Huxley model, which was subsequently analyzed in electrical circuit terms by J. Nagumo and others. Whereas the FitzHugh-Nagumo equations are not intended to capture the physiological properties of the neuron as directly as the original Hodgkin-Huxley equations do, this simplified model is important because it displays much of the qualitative behavior characteristic of neuron electrical activity, while offering the advantage of being considerably easier to study. FitzHugh’s model actually is a generalization of van der Pol’s equation (6). You can show that introduction of the variable y=1μx'+13x3−x $y = \frac{1}{μ} x ′ + \frac{1}{3} x^{3} - x$ in van der Pol’s equation (which results in better phase plane analysis than does simply taking y=x' $y = x ′$ ) leads to the system

x' = μ (y + x - 1 3 x 3), y' = - 1 μ x,

$\begin{array}{l} x ′ = μ (y + x - \frac{1}{3} x^{3}), \\ y ′ = - \frac{1}{μ} x, \end{array}$

which FitzHugh generalized by adding terms:

x' = μ (y + x - 1 3 x 3 + I), y' = - 1 μ (x - a + b y) .

$\begin{array}{l} x ′ = μ (y + x - \frac{1}{3} x^{3} + I), \\ y ′ = - \frac{1}{μ} (x - a + b y) . \end{array}$

Here a and b are constants and I is a function of the time t. Loosely speaking, x(t) behaves in a manner similar to the neuron membrane potential, I(t) is the electrical stimulus applied to the neuron, and y(t) is a composite of the other three variables in the Hodgkin-Huxley model. To simulate neuron electrical activity, we will use FitzHugh’s values a=0.7, b=0.8, $a = 0.7, b = 0.8,$ and μ=3, $μ = 3,$ while assigning various constant values to the stimulus I(t).

First, with I(t)≡0 $I (t) \equiv 0$ (corresponding to the resting state of the neuron), you can verify that the system (7) has exactly one equilibrium point at roughly x=1.1994 $x = 1.1994$ and y=−0.6243. $y = - 0.6243 .$ What is striking is the way in which the system responds as I becomes nonzero (corresponding to electrical stimulation of the neuron). Figure 9.4.25 shows the solution curves of the system corresponding to the three constant values I(t)≡−0.15, I(t)≡−0.17, $I (t) \equiv - 0.15, I (t) \equiv - 0.17,$ and I(t)≡−0.5. $I (t) \equiv - 0.5 .$ The graph on the left gives the phase plane for x and y, whereas the graph on the right shows x(t) as a function of t. All curves begin at time t=0 $t = 0$ at the original equilibrium point (1.1994,−0.6243) $(1.1994, - 0.6243)$ indicated in the graph on the left.

FIGURE 9.4.25.

Solutions of the FitzHugh-Nagumo equations (7) with three constant values of the electrical stimulus `I`(`t`), using a=0.7,b=0.8, $a = 0.7, b = 0.8,$ and μ=3 $μ = 3$ .

When the stimulus I(t) is held at the constant value −0.15, $- 0.15,$ x (which is analogous to the neuron membrane potential) varies slightly from its rest value, but soon finds a new “perturbed” equilibrium at which it then remains (thin blue curves); this mirrors the behavior of the membrane potential when the neuron receives a stimulus insufficiently large to generate an action potential. The response of the system differs dramatically, however, when the constant stimulus is decreased slightly to −0.17 $- 0.17$ ; once again x finds a new equilibrium, but only after exhibiting wide swings downward and back upward (dashed curves); this is suggestive of the firing of a single action potential. Finally, when I(t)≡−0.5, $I (t) \equiv - 0.5,$ x oscillates repeatedly, in a manner reminiscent of both the Rayleigh and van der Pol systems (thick blue curves); this corresponds to repetitive firing of the neuron.

After using your own computer system’s ODE solver to verify these behaviors, you can investigate what happens with other constant nonzero values of the stimulus I(t). Do all such values lead either to oscillatory phase plane solutions or to ones that converge to the same perturbed equilibrium point? Or do certain different values lead to different perturbed equilibrium points? Do all oscillatory solutions correspond to phase plane curves that appear to converge to a single limit cycle?

The FitzHugh-Nagumo system has proven to be a very useful simplification of the Hodgkin-Huxley system, exhibiting a number of characteristics of neuron electrical activity. For a more detailed discussion see the classic work of L. Edelstein-Keshet, Mathematical Models in Biology (Society for Industrial and Applied Mathematics, 2005).

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 9.4 Nonlinear Mechanical Systems

Create new playlist

Sign In

Sign Up

Table of Contents for
9.4 Nonlinear Mechanical Systems