10.3 Translation and Partial Fractions

As illustrated by Examples 1 and 2 of Section 10.2, the solution of a linear differential equation with constant coefficients can often be reduced to the matter of finding the inverse Laplace transform of a rational function of the form

R(s)=P(s)Q(s)
(1)

where the degree of P(s) is less than that of Q(s). The technique for finding L−1{R(s)} is based on the same method of partial fractions that we use in elementary calculus to integrate rational functions. The following two rules describe the partial fraction decomposition of R(s), in terms of the factorization of the denominator Q(s) into linear factors and irreducible quadratic factors corresponding to the real and complex zeros, respectively, of Q(s).

Finding L−1{R(s)} involves two steps. First we must find the partial fraction decomposition of R(s), and then we must find the inverse Laplace transform of each of the individual partial fractions of the types that appear in (2) and (3). The latter step is based on the following elementary property of Laplace transforms.

Proof:

If we simply replace s with s−a in the definition of F(s)=L{f(t)}, we obtain

F(s−a)=∫0∞e−(s−a)tf(t)dt=∫0∞e−st[eatf(t)]dt=L{eatf(t)}.

This is Eq. (4), and it is clear that Eq. (5) is the same.

If we apply the translation theorem to the formulas for the Laplace transforms of tn, cos kt, and sin kt that we already know—multiplying each of these functions by eat and replacing s with s−a in the transforms—we get the following additions to the table in Fig. 10.1.2.

f(t) F(s)
eattn n!(s−a)n+1 (s>a) (6)
eat cos kt s−a(s−a)2+k2 (s>a) (7)
eat sin kt k(s−a)2+k2 (s>a) (8)

For ready reference, all the Laplace transforms derived in this chapter are listed in the table of transforms that appears in the endpapers.

FIGURE 10.3.1.

The mass–spring–dashpot system of Example 1.

Example 1

Damped mass-spring system Consider a mass-and-spring system with m=12, k=17, and c=3 in mks units (Fig. 10.3.1). As usual, let x(t) denote the displacement of the mass m from its equilibrium position. If the mass is set in motion with x(0)=3 and x′(0)=1, find x(t) for the resulting damped free oscillations.

Solution

The differential equation is 12x″+3x′+17x=0, so we need to solve the initial value problem

x″+6x′+34x=0;x(0)=3,x′(0)=1.

We take the Laplace transform of each term of the differential equation. Because (obviously) L{0}≡0, we get the equation

[s2X(s)−3s−1]+6[sX(s)−3]+34X(s)=0,

which we solve for

X(s)=3s+19s2+6s+34=3⋅s+3(s+3)2+25+2⋅5(s+3)2+25.

Applying the formulas in (7) and (8) with a=−3 and k=5, we now see that

x(t)=e−3t(3 cos 5t+2 sin 5t).

Figure 10.3.2 shows the graph of this rapidly decaying damped oscillation.

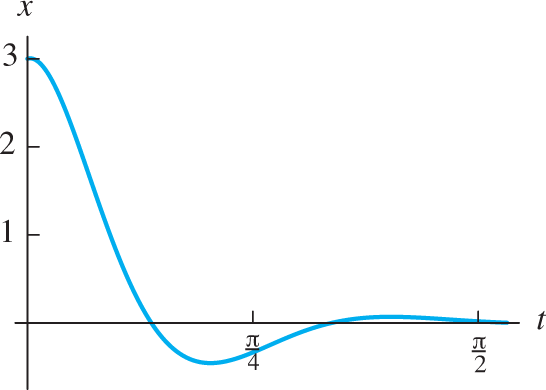
FIGURE 10.3.2.

The position function x(t) in Example 1.

Example 2 illustrates a useful technique for finding the partial fraction coefficients in the case of nonrepeated linear factors.

Example 2

Find the inverse Laplace transform of

R(s)=s2+1s3−2s2−8s.

Solution

Note that the denominator of R(s) factors as Q(s)=s(s+2)(s−4). Hence

s2+1s3−2s2−8s=As+Bs+2+Cs−4.

Multiplication of each term of this equation by Q(s) yields

s2+1=A(s+2)(s−4)+Bs(s−4)+Cs(s+2).

When we successively substitute the three zeros s=0, s=−2, and s=4 of the denominator Q(s) in this equation, we get the results

−8A=1,12B=5,and24C=17.

Thus A=−18, B=512, and C=1724, so

s2+1s3−2s2−8s=−18s+512s+2+1724s−4,

and therefore

L−1{s2+1s3−2s2−8s}=−18+512e−2t+1724e4t.

Example 3 illustrates a differentiation technique for finding the partial fraction coefficients in the case of repeated linear factors.

Example 3

Solve the initial value problem

y″+4y′+4y=t2;y(0)=y′(0)=0.

Solution

The transformed equation is

s2Y(s)+4sY(s)+4Y(s)=2s3.

Thus

Y(s)=2s3(s+2)2=As3+Bs2+Cs+D(s+2)2+Es+2.
(9)

To find A, B, and C, we multiply both sides by s3 to obtain

2(s+2)2=A+Bs+Cs2+s3F(s),
(10)

where F(s)=D(s+2)−2+E(s+2)−1 is the sum of the two partial fractions corresponding to (s+2)2. Substitution of s=0 in Eq. (10) yields A=12. To find B and C, we differentiate Eq. (10) twice to obtain

−4(s+2)3=B+2Cs+3s2F(s)+s3F′(s)
(11)

and

12(s+2)4=2C+6sF(s)+6s2F′(s)+s3F″(s).
(12)

Now substitution of s=0 in Eq. (11) yields B=−12, and substitution of s=0 in Eq. (12) yields C=38.

To find D and E, we multiply each side in Eq. (9) by (s+2)2 to get

2s3=D+E(s+2)+(s+2)2G(s).
(13)

where G(s)=As−3+Bs−2+Cs−1, and then differentiate to obtain

−6s4=E+2(s+2)G(s)+(s+2)2G′(s).
(14)

Substitution of s=−2 in Eqs. (13) and (14) now yields D=−14 and E=−38. Thus

Y(s)=12s3−12s2+38s−14(s+2)2−38s+2,

so the solution of the given initial value problem is

y(t)=14t2−12t+38−14te−2t−38e−2t.

Examples 4, 5, and 6 illustrate techniques for dealing with quadratic factors in partial fraction decompositions.

Example 4

Mass–spring–dashpot system Consider the mass–spring–dashpot system as in Example 1, but with initial conditions x(0)=x′(0)=0 and with the imposed external force F(t)=15 sin 2t. Find the resulting transient motion and steady periodic motion of the mass.

Solution

The initial value problem we need to solve is

x″+6x′+34x=30sin 2t;x(0)=x′(0)=0.

The transformed equation is

s2X(s)+6sX(s)+34X(s)=60s2+4.

Hence

X(s)=60(s2+4)[(s+3)2+25]=As+Bs2+4+Cs+D(s+3)2+25.

When we multiply both sides by the common denominator, we get

60=(As+B)[(s+3)2+25]+(Cs+D)(s2+4).
(15)

To find A and B, we substitute the zero s=2i of the quadratic factor s2+4 in Eq. (15); the result is

60=(2iA+B)[(2i+3)2+25],

which we simplify to

60=(−24A+30B)+(60A+12B)i.

We now equate real parts and imaginary parts on each side of this equation to obtain the two linear equations

−24A+30B=60and60A+12B=0,

which are readily solved for A=−1029 and B=5029.

To find C and D, we substitute the zero s=−3+5i of the quadratic factor (s+3)2+25 in Eq. (15) and get

60=[C(−3+5i)+D][(−3+5i)2+4],

which we simplify to

60=(186C−12D)+(30C−30D)i.

Again we equate real parts and imaginary parts; this yields the two linear equations

186C−12D=60and30C−30D=0,

and we readily find their solution to be C=D=1029.

With these values of the coefficients A, B, C, and D, our partial fractions decomposition of X(s) is

X(s)=129(−10s+50s2+4+10s+10(s+3)2+25)=129(−10s+25⋅2s2+4+10(s+3)−4⋅5(s+3)2+25).

After we compute the inverse Laplace transforms, we get the position function

x(t)=529(−2 cos 2t+5 sin 2t)+229e−3t(5 cos 5t−2 sin 5t).

The terms of circular frequency 2 constitute the steady periodic forced oscillation of the mass, whereas the exponentially damped terms of circular frequency 5 constitute its transient motion, which disappears very rapidly (see Fig. 10.3.3). Note that the transient motion is nonzero even though both initial conditions are zero.

FIGURE 10.3.3.

The periodic forced oscillation xsp(t), damped transient motion xtr(t), and solution x(t)=xsp(t)+xtr(t) in Example 4.

Resonance and Repeated Quadratic Factors

The following two inverse Laplace transforms are useful in inverting partial fractions that correspond to the case of repeated quadratic factors:

L−1{s(s2+k2)2}=12ktsinkt,
(16)
L−1{s(s2+k2)2}=12k3(sinkt−ktcoskt).
(17)

These follow from Example 5 and Problem 31 of Section 10.2, respectively. Because of the presence in Eqs. (16) and (17) of the terms tsin kt and tcos kt, a repeated quadratic factor ordinarily signals the phenomenon of resonance in an undamped mechanical or electrical system.

Example 5

Use Laplace transforms to solve the initial value problem

x″+ω02x=F0sinωt;x(0)=0=x′(0)

that determines the undamped forced oscillations of a mass on a spring.

Solution

When we transform the differential equation, we get the equation

s2X(s)+ω02X(s)=F0ωs2+ω2,soX(s)=F0ω(s2+ω2)(s2+ω02).

If ω≠ω0, we find without difficulty that

X(s)=F0ωω2−ω02(1s2+ω02−1s2+ω2),

so it follows that

x(t)=F0ωω2−ω02(1ω0sinω0t−1ωsinωt).

But if ω=ω0, we have

X(s)=F0ω0(s2+ω02)2,

so Eq. (17) yields the resonance solution

x(t)=F02ω02(sinω0t−ω0tcosω0t).
(18)

Remark

The solution curve defined in Eq. (18) bounces back and forth (see Fig. 10.3.4) between the “envelope curves” x=±C(t) that are obtained by writing (18) in the form

x(t)=A(t)cosω0t+B(t)sinω0t

and then defining the usual “amplitude” C=A2+B2. In this case we find that

C(t)=F02ω02ω02t2+1.

This technique for constructing envelope curves of resonance solutions is illustrated further in the application material for this section.

FIGURE 10.3.4.

The resonance solution in (18) with ω0=12 and F0=1, together with its envelope curves x=±C(t).

Example 6

Solve the initial value problem

y(4)+2y″+y=4tet;y(0)=y′(0)=y″(0)=y(3)(0)=0.

Solution

First we observe that

L{y″(t)}=s2Y(s),L{y(4)(t)}=s4Y(s),andL{tet}=1(s−1)2.

Hence the transformed equation is

(s4+2s2+1)Y(s)=4(s−1)2.

Thus our problem is to find the inverse transform of

Y(s)=4(s−1)2(s2+1)2=A(s−1)2+Bs−1+Cs+D(s2+1)2+Es+Fs2+1.
(19)

If we multiply by the common denominator (s−1)2(s2+1)2, we get the equation

A(s2+1)2+B(s−1)(s2+1)2+Cs(s−1)2+D(s−1)2+Es(s−1)2(s2+1)+F(s−1)2(s2+1)=4.
(20)

Upon substituting s=1 we find that A=1.

Equation (20) is an identity that holds for all values of s. To find the values of the remaining coefficients, we substitute in succession the values s=0, s=−1, s=2, s=−2, and s=3 in Eq. (20). This yields the system

−B+D+F=3,−8B−4C+4D−8E+8F=0,25B+2C+D+10E+5F=−21,−75B−18C+9D−90E+45F=−21,200B+12C+4D+120E+40F=−96
(21)

of five linear equations in B, C, D, E, and F. With the aid of a calculator programmed to solve linear systems, we find that B=−2, C=2, D=0, E=2, and F=1.

We now substitute in Eq. (19) the coefficients we have found, and thus obtain

Y(s)=1(s−1)2−2s−1+2s(s2+1)2+2s+1s2+1.

Recalling Eq. (16), the translation property, and the familiar transforms of cos t and sin t, we see finally that the solution of the given initial value problem is

y(t)=(t−2)et+(t+1) sin t+2 cos t.

10.3 Problems

Apply the translation theorem to find the Laplace transforms of the functions in Problems 1 through 4.

  1. f(t)=t4eπt

     

  2. f(t)=t3/2e−4t

     

  3. f(t)=e−2tsin 3πt

     

  4. f(t)=e−t/2cos 2(t−18π)

Apply the translation theorem to find the inverse Laplace transforms of the functions in Problems 5 through 10.

  1. F(s)=32s−4

     

  2. F(s)=s−1(s+1)3

     

  3. F(s)=1s2+4s+4

     

  4. F(s)=s+2s2+4s+5

     

  5. F(s)=3s+5s2−6s+25

     

  6. F(s)=2s−39s2−12s+20

Use partial fractions to find the inverse Laplace transforms of the functions in Problems 11 through 22.

  1. F(s)=1s2−4

     

  2. F(s)=5s−6s2−3s

     

  3. F(s)=5−2ss2+7s+10

     

  4. F(s)=5s−4s3−s2−2s

     

  5. F(s)=1s3−5s2

     

  6. F(s)=1(s2+s−6)2

     

  7. F(s)=1s4−16

     

  8. F(s)=s3(s−4)4

     

  9. F(s)=s2−2ss4+5s2+4

     

  10. F(s)=1s4+8s2+16

     

  11. F(s)=s2+3(s2+2s+2)2

     

  12. F(s)=2s3−s2(4s2−4s+5)2

Use the factorization

s4+4a4=(s2−2as+2a2)(s2+2as+2a2)

to derive the inverse Laplace transforms listed in Problems 23 through 26.

  1. L−1{s3s4+4a4}=cosh atcos at

     

  2. L−1{ss4+4a4}=12a2sinhatsinat

     

  3. L−1{s2s4+4a4}=12a(cosh atsin at+sinh atcos at)

     

  4. L−1{1s4+4a4}=14a3(cosh atsin at−sinh atcos at)

Use Laplace transforms to solve the initial value problems in Problems 27 through 38.

  1. x″+6x′+25x=0; x(0)=2, x′(0)=3

     

  2. x″−6x′+8x=2; x(0)=x′(0)=0

     

  3. x″−4x=3t; x(0)=x′(0)=0

     

  4. x″+4x′+8x=e−t; x(0)=x′(0)=0

     

  5. x(3)+x″−6x′=0; x(0)=0, x′(0)=x″(0)=1

     

  6. x(4)−x=0; x(0)=1, x′(0)=x″(0)=x(3)(0)=0

     

  7. x(4)+x=0; x(0)=x′(0)=x″(0)=0, x(3)(0)=1

     

  8. x(4)+13x″+36x=0; x(0)=x″(0)=0, x′(0)=2, x(3)(0)=−13

     

  9. x(4)+8x″+16x=0; x(0)=x′(0)=x″(0)=0, x(3)(0)=1

     

  10. x(4)+2x″+x=e2t; x(0)=x′(0)=x″(0)=x(3)(0)=0

     

  11. x″+4x′+13x=te−t; x(0)=0, x′(0)=2

     

  12. x″+6x′+18x=cos 2t; x(0)=1, x′(0)=−1

Resonance

Problems 39 and 40 illustrate two types of resonance in a mass–spring–dashpot system with given external force F(t) and with the initial conditions x(0)=x′(0)=0.

  1. Suppose that m=1, k=9, c=0, and F(t)=6 cos 3t. Use the inverse transform given in Eq. (16) to derive the solution x(t)=tsin 3t. Construct a figure that illustrates the resonance that occurs.

  2. Suppose that m=1, k=9.04, c=0.4, and F(t)=6e−t/5 cos 3t. Derive the solution

    x(t)=te−t/5sin 3t.

    Show that the maximum value of the amplitude function A(t)=te−t/5 is A(5)=5/e. Thus (as indicated in Fig. 10.3.5) the oscillations of the mass increase in amplitude during the first 5 s before being damped out as t→+∞.

    FIGURE 10.3.5.

    The graph of the damped oscillation in Problem 40.

10.3 Application Damping and Resonance Investigations

Here we outline a Maple investigation of the behavior of the mass–spring–dashpot system

mx″+cx′+kx=F(t), x(0)=x′(0)=0
(1)

with parameter values

m := 25; c := 10; k := 226;

in response to a variety of possible external forces:

  1. F(t)≡226

This should give damped oscillations “leveling off” to a constant solution (why?).

  1. F(t)=901 cos 3t

With this periodic external force you should see a steady periodic oscillation with an exponentially damped transient motion (as illustrated in Fig. 5.6.13).

  1. F(t)=900e−t/5 cos 3t

Now the periodic external force is exponentially damped, and the transform X(s) includes a repeated quadratic factor that signals the presence of a resonance phenomenon. The response x(t) isa constant multiple of that shown in Fig. 10.3.5.

  1. F(t)=900te−t/5 cos 3t

We have inserted the factor t to make it a bit more interesting. The solution in this case is illustrated below.

  1. F(t)=162t3e−t/5 cos 3t

In this case you’ll find that the transform X(s) involves the fifth power of a quadratic factor, and its inverse transform by manual methods would be impossibly tedious.

To illustrate the Maple approach, we first set up the differential equation corresponding to Case 4.

F := 900*t*exp(t/5) *cos(3* t);
de := m* diff(x(t),t$2) + c* diff(x(t),t) + k* x(t) = F;

Then we apply the Laplace transform and substitute the initial conditions.

with(inttrans):
DE := laplace(de, t, s):
X(s) := solve(DE, laplace(x(t), t, s)):
X(s) := simplify(subs(x(0)=0, D(x)(0)=0, X(s)));

At this point the command factor(denom(X(s))) shows that

X(s)=22500(25s2+10s−224)(25s2+10s+226)3.

The cubed quadratic factor would be difficult to handle manually, but the command

x(t) := invlaplace(X(s), s, t);

soon yields

x(t)=e−t/5(tcos 3t+(3t2−13)sin 3t).

The amplitude function for these damped oscillations is defined by

C(t) := exp(-t/5)*sqrt(t^2 + (3*t^2 1/3)^2);

and finally the command

plot({x(t), C(t), -C(t)}, t=0..40);

produces the plot shown in Fig. 10.3.6. The resonance resulting from the repeated quadratic factor consists of a temporary buildup before the oscillations are damped out.

FIGURE 10.3.6.

The resonance solution and its envelope curves in Case 4.

For a similar solution in one of the other cases listed previously, you need only enter the appropriate force F in the initial command above and then re-execute the subsequent commands. To see the advantage of using Laplace transforms, set up the differential equation de for Case 5 and examine the result of the command

dsolve({de, x(0)=0, D(x)(0)=0}, x(t));

Of course you can substitute your own favorite mass–spring–dashpot parameters for those used here. But it will simplify the calculations if you choose m, c, and k so that

mr2+cr+k=(pr+a)2+b2
(2)

where p, a, and b are integers. One way is to select the latter integers first, then use Eq. (2) to determine m, c, and k.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.
Reset
3.149.253.239