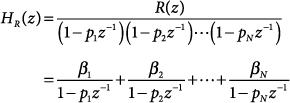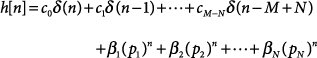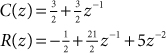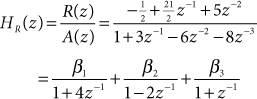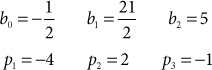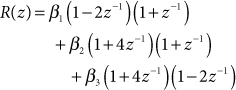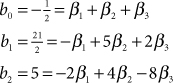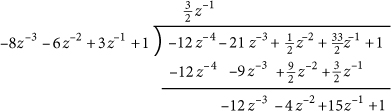Note 47. Inverse z Transform via Partial Fraction Expansion:
Case 2: All Poles Distinct with M ≥ N in System Function (Explicit Approach)
This note presents a procedure for computing the inverse z transform for system functions in which all poles are distinct and the degree, M, of the numerator equals or exceeds the degree, N, of the denominator. The procedure uses polynomial division to convert the improper rational function, H(z), into the sum of a polynomial, C(z), and a proper rational function, HR(z).
In order for a rational function to be expanded as a sum of partial-fraction terms, the degree of the numerator must be less than the degree of the denominator. In cases where M ≥ N, the system function must be restructured as the sum of a polynomial, C(z), and a proper rational function, HR(z):
47.1
where
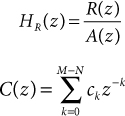
This restructuring can be implemented by solving directly for the values of the coefficients in C(z) and R(z) using polynomial division, and then forming a partial fraction expansion for just HR(z) instead of for H(z). This approach is detailed in Design Procedure 47.1 and is demonstrated in Example 47.1. Polynomial division is detailed in Math Box 47.1 on the next page.
Design Procedure 47.1. Partial Fraction Expansion: Simple Pole Case with M ≥ N Solving Explicitly for C(z) and R(z)
The system function is an improper rational function if the order, M, of the numerator polynomial equals or exceeds the order, N, of the denominator polynomial. This procedure is based on explicitly restructuring the system function as the sum of a polynomial, C(z), and a proper rational function, HR(z) = R(z)/A(z):
DP 47.1
- Use polynomial division, as described in Math Box (47.1), to determine the coefficients for C(z) and R(z). The quotient produced by the division is C(z), and the remainder is R(z).
- Construct the partial fraction expansion for HR(z):
DP 47.2
- Use Design Procedure 46.1 from Note 46 to solve for the N values of βk.
- Using values for ck obtained in step 1, and the values for βk obtained in step 3, the filter’s unit sample response, h[n], can be written as
DP 47.3
Example 47.2. Explicitly Solving for a New Numerator When H(z) Is Improper
Consider the system function given by
47.2
The corresponding unit sample response can be determined using Design Procedure 47.1. Polynomial division can be used, as in Math Box 47.1, to solve for C(z) and R(z) explicitly:
Then we only need to expand the proper rational function that is based on the remainder of the division operation:
47.3
Comparing Eq. (47.2) to Eq. (DP 46.1) from Note 46 reveals that
Adding the right-hand side of Eq. (47.2) yields a numerator of
47.4
Setting coefficients from Eq. (47.3) equal to coefficients from Eq. (47.2) for like powers of z yields the system of equations
Math Box 47.1. Polynomial Division
Consider the system function given by
For purposes of computing the inverse z transform, the goal of polynomial division is to eliminate from the numerator terms involving z–k for k ≥ N, where N is the most negative degree of z in the denominator. This goal is best accomplished by reversing the order of the polynomials before beginning the division:
Begin by dividing the dividend’s first term, –12z–4, by the divisior’s first term, –8z–3. The result is 
, so we multiply the divisor by 
and subtract the result from the dividend:
We can call the result of this subtraction the working remainder. The terms appearing above the division symbol comprise the quotient. Next, divide the first term (–12z–3) of the working remainder by the first term (–8z–3) of the divisor. The result is 
. Therefore, we multiply the divisor by and subtract the result from the working remainder to obtain a new working remainder:
The process stops when the highest power of z–1 in the divisor is greater than the highest power of z–1 in the working remainder. The working remainder when the process stops becomes the new numerator in the fractional part of the system function. The quotient becomes the new non-fractional C(z), and we can rewrite the system function as
