Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

1.6 Substitution Methods and Exact Equations

The first-order differential equations we have solved in the previous sections have all been either separable or linear. But many applications involve differential equations that are neither separable nor linear. In this section we illustrate (mainly with examples) substitution methods that sometimes can be used to transform a given differential equation into one that we already know how to solve.

For instance, the differential equation

d y d x = f (x, y),

$\frac{d y}{d x} = f (x, y),$ (1)

with dependent variable y and independent variable x, may contain a conspicuous combination

v = α (x, y)

$v = α (x, y)$ (2)

of x and y that suggests itself as a new independent variable v. Thus the differential equation

d y d x = (x + y + 3) 2

$\frac{d y}{d x} = {(x + y + 3)}^{2}$

practically demands the substitution v=x+y+3 $v = x + y + 3$ of the form in Eq. (2).

If the substitution relation in Eq. (2) can be solved for

y = β (x, v),

$y = β (x, v),$ (3)

then application of the chain rule—regarding v as an (unknown) function of x—yields

d y d x = \partial β \partial x d x d x + \partial β \partial v d v d x = β x + β v d v d x,

$\frac{d y}{d x} = \frac{\partial β}{\partial x} \frac{d x}{d x} + \frac{\partial β}{\partial v} \frac{d v}{d x} = β_{x} + β_{v} \frac{d v}{d x},$ (4)

where the partial derivatives ∂β/∂x=βx(x,v) $\partial β / \partial x = β_{x} (x, v)$ and ∂β/∂v=βv(x,v) $\partial β / \partial v = β_{v} (x, v)$ are known functions of x and v. If we substitute the right-hand side in (4) for dy/dx $d y / d x$ in Eq. (1) and then solve for dv/dx $d v / d x$ , the result is a new differential equation of the form

d v d x = g (x, v)

$\frac{d v}{d x} = g (x, v)$ (5)

with new dependent variable v. If this new equation is either separable or linear, then we can apply the methods of preceding sections to solve it.

If v=v(x) $v = v (x)$ is a solution of Eq. (5), then y=β(x,v(x)) $y = β (x, v (x))$ will be a solution of the original Eq. (1). The trick is to select a substitution such that the transformed Eq. (5) is one we can solve. Even when possible, this is not always easy; it may require a fair amount of ingenuity or trial and error.

Example 1

Solve the differential equation

d y d x = (x + y + 3) 2 .

$\frac{d y}{d x} = {(x + y + 3)}^{2} .$

Solution

As indicated earlier, let’s try the substitution

v = x + y + 3; that is, y = v - x - 3 .

$\begin{array}{l} v = x + y + 3; & that is, & y = v - x - 3 . \end{array}$

Then

d y d x = d v d x - 1,

$\frac{d y}{d x} = \frac{d v}{d x} - 1,$

so the transformed equation is

d v d x = 1 + v 2 .

$\frac{d v}{d x} = 1 + v^{2} .$

This is a separable equation, and we have no difficulty in obtaining its solution

x = \int d v 1 + v 2 = tan - 1 v + C .

$x = \int \frac{d v}{1 + v^{2}} = \tan^{- 1} v + C .$

So v=tan(x−C) $v = \tan (x - C)$ . Because v=x+y+3 $v = x + y + 3$ , the general solution of the original equation dy/dx=(x+y+3)2 $d y / d x = {(x + y + 3)}^{2}$ is x+y+3=tan(x−C) $x + y + 3 = \tan (x - C)$ ; that is,

y (x) = tan (x - C) - x - 3 .

$y (x) = \tan (x - C) - x - 3 .$

Remark

Figure 1.6.1 shows a slope field and typical solution curves for the differential equation of Example 1. We see that, although the function f(x,y)=(x+y+3)2 $f (x, y) = {(x + y + 3)}^{2}$ is continuously differentiable for all x and y, each solution is continuous only on a bounded interval. In particular, because the tangent function is continuous on the open interval (−π/2,π/2) $(- π / 2, π / 2)$ , the particular solution with arbitrary constant value C is continuous on the interval where −π/2<x−C<π/2 $- π / 2 < x - C < π / 2$ ; that is, C−π/2<x<C+π/2 $C - π / 2 < x < C + π / 2$ . This situation is fairly typical of nonlinear differential equations, in contrast with linear differential equations, whose solutions are continuous wherever the coefficient functions in the equation are continuous.

FIGURE 1.6.1.

Slope field and solution curves for y'=(x+y+3)2 $y ′ = {(x + y + 3)}^{2}$ .

Example 1 illustrates the fact that any differential equation of the form

dydx=F(ax+by+c) $\frac{d y}{d x} = F (a x + b y + c)$ (6)

can be transformed into a separable equation by use of the substitution v=ax+by+c $v = a x + b y + c$ (see Problem 55). The paragraphs that follow deal with other classes of first-order equations for which there are standard substitutions that are known to succeed.

Homogeneous Equations

A homogeneous first-order differential equation is one that can be written in the form

d y d x = F (y x) .

$\frac{d y}{d x} = F (\frac{y}{x}) .$ (7)

If we make the substitutions

v = y x, y = v x, d y d x = v + x d v d x,

$v = \frac{y}{x}, y = v x, \frac{d y}{d x} = v + x \frac{d v}{d x},$ (8)

then Eq. (7) is transformed into the separable equation

x d v d x = F (v) - v .

$x \frac{d v}{d x} = F (v) - v .$

Thus every homogeneous first-order differential equation can be reduced to an integration problem by means of the substitutions in (8).

Remark

A dictionary definition of “homogeneous” is “of a similar kind or nature.” Consider a differential equation of the form

A x m y n d y d x = B x p y q + C x r y s,

$A x^{m} y^{n} \frac{d y}{d x} = B x^{p} y^{q} + C x^{r} y^{s},$ (*)

whose polynomial coefficient functions are “homogeneous” in the sense that each of their terms has the same total degree, m+n=p+q=r+s=K $m + n = p + q = r + s = K$ . If we divide each side of (*) $(*)$ by xK $x^{K}$ , then the result—because xmyn/xm+n=(y/x)n $x^{m} y^{n} / x^{m + n} = {(y / x)}^{n}$ , and so forth—is the equation

A (y x) n d y d x = B (y x) q + C (y x) s,

$A {(\frac{y}{x})}^{n} \frac{d y}{d x} = B {(\frac{y}{x})}^{q} + C {(\frac{y}{x})}^{s},$

which evidently can be written (by another division) in the form of Eq. (7). More generally, a differential equation of the form P(x,y)y'=Q(x,y) $P (x, y) y ′ = Q (x, y)$ with polynomial coefficients P and Q is homogeneous if the terms in these polynomials all have the same total degree K. The differential equation in the following example is of this form with K=2 $K = 2$ .

Example 2

Solve the differential equation

2 x y d y d x = 4 x 2 + 3 y 2 .

$2 x y \frac{d y}{d x} = 4 x^{2} + 3 y^{2} .$

Solution

This equation is neither separable nor linear, but we recognize it as a homogeneous equation by writing it in the form

d y d x = 4 x 2 + 3 y 2 2 x y = 2 (x y) + 3 2 (y x) .

$\frac{d y}{d x} = \frac{4 x^{2} + 3 y^{2}}{2 x y} = 2 (\frac{x}{y}) + \frac{3}{2} (\frac{y}{x}) .$

The substitutions in (8) then take the form

y = v x, d y d x = v + x d v d x, v = y x, and 1 v = x y .

$\begin{array}{l} \begin{array}{l} y = v x, & \frac{d y}{d x} = v + x \frac{d v}{d x}, & v = \frac{y}{x}, & and & \frac{1}{v} = \frac{x}{y} . \end{array} \end{array}$

These yield

v + x d v d x = 2 v + 3 2 v,

$v + x \frac{d v}{d x} = \frac{2}{v} + \frac{3}{2} v,$

and hence

x d v d x \int 2 v v 2 + 4 d v ln (v 2 + 4) = = = 2 v + v 2 = v 2 + 4 2 v; \int 1 x d x; ln | x | + ln C .

$\begin{array}{rcl} x \frac{d v}{d x} & = & \frac{2}{v} + \frac{v}{2} = \frac{v^{2} + 4}{2 v}; \\ \int \frac{2 v}{v^{2} + 4} d v & = & \int \frac{1}{x} d x; \\ \ln (v^{2} + 4) & = & \ln | x | + \ln C . \end{array}$

We apply the exponential function to both sides of the last equation to obtain

v 2 + 4 y 2 x 2 + 4 y 2 + 4 x 2 = = = C | x |; C | x |; k x 3 .

$\begin{array}{rcl} v^{2} + 4 & = & C | x |; \\ \frac{y^{2}}{x^{2}} + 4 & = & C | x |; \\ y^{2} + 4 x^{2} & = & k x^{3} . \end{array}$

Note that the left-hand side of this equation is necessarily nonnegative. It follows that k>0 $k > 0$ in the case of solutions that are defined for x>0 $x > 0$ , while k<0 $k < 0$ for solutions where x<0 $x < 0$ . Indeed, the family of solution curves illustrated in Fig. 1.6.2 exhibits symmetry about both coordinate axes. Actually, there are positive-valued and negative-valued solutions of the forms y(x)=±kx3−4x2−−−−−−−−√ $y (x) = \pm \sqrt{{k x}^{3} - 4 x^{2}}$ that are defined for x>4/k $x > 4 / k$ if the constant k is positive, and for x<4/k $x < 4 / k$ if k is negative.

FIGURE 1.6.2.

Slope field and solution curves for 2xyy'=4x2+3y2 $2 x y y ′ = 4 x^{2} + 3 y^{2}$ .

Example 3

Solve the initial value problem

x d y d x = y + x 2 - y 2 - - - - - - \sqrt, y (x 0) = 0,

$x \frac{d y}{d x} = y + \sqrt{x^{2} - y^{2}}, y (x_{0}) = 0,$

where x0>0 $x_{0} > 0$ .

Solution

We divide both sides by x and find that

d y d x = y x + 1 - (y x) 2 - - - - - - - - \sqrt,

$\frac{d y}{d x} = \frac{y}{x} + \sqrt{1 - {(\frac{y}{x})}^{2}},$

so we make the substitutions in (8); we get

v + x d v d x \int 1 1 - v 2 \sqrt d v sin - 1 v = = = v + 1 - v 2 - - - - - \sqrt; \int 1 x d x; ln x + C .

$\begin{array}{rcl} v + x \frac{d v}{d x} & = & v + \sqrt{1 - v^{2}}; \\ \int \frac{1}{\sqrt{1 - v^{2}}} d v & = & \int \frac{1}{x} d x; \\ \sin^{- 1} v & = & \ln x + C . \end{array}$

We need not write ln |x| $\ln | x |$ because x>0 $x > 0$ near x=x0>0 $x = x_{0} > 0$ . Now note that v(x0)=y(x0)/x0=0 $v (x_{0}) = y (x_{0}) / x_{0} = 0$ , so C=sin−10−ln x0=−ln x0 $C = \sin^{- 1} 0 - \ln x_{0} = - \ln x_{0}$ . Hence

v = y x = sin (ln x - ln x 0) = sin (ln x x 0) .

$v = \frac{y}{x} = \sin (\ln x - \ln x_{0}) = \sin (\ln \frac{x}{x_{0}}) .$

and therefore

y (x) = x sin (ln x x 0)

$y (x) = x \sin (\ln \frac{x}{x_{0}})$

is the desired particular solution. Figure 1.6.3 shows some typical solution curves. Because of the radical in the differential equation, these solution curves are confined to the indicated triangular region x≧|y|. $x ≧ | y | .$ You can check that the boundary lines y=x $y = x$ and y=−x $y = - x$ (for x>0 $x > 0$ ) are singular solution curves that consist of points of tangency with the solution curves found earlier.

FIGURE 1.6.3.

Solution curves for xy'=y+x2−y2−−−−−−√. $x y ′ = y + \sqrt{x^{2} - y^{2}} .$

Bernoulli Equations

A first-order differential equation of the form

d y d x + P (x) y = Q (x) y n

$\frac{d y}{d x} + P (x) y = Q (x) y^{n}$ (9)

is called a Bernoulli equation. If either n=0 $n = 0$ or n=1 $n = 1$ , then Eq. (9) is linear. Otherwise, as we ask you to show in Problem 56, the substitution

v = y 1 - n

$v = y^{1 - n}$ (10)

transforms Eq. (9) into the linear equation

dvdx+(1−n)P(x)v=(1−n)Q(x). $\frac{d v}{d x} + (1 - n) P (x) v = (1 - n) Q (x) .$

Rather than memorizing the form of this transformed equation, it is more efficient to make the substitution in Eq. (10) explicitly, as in the following examples.

Example 4

If we rewrite the homogeneous equation 2xyy'=4x2+3y2 $2 x y y ′ = 4 x^{2} + 3 y^{2}$ of Example 2 in the form

d y d x - 3 2 x y = 2 x y,

$\frac{d y}{d x} - \frac{3}{2 x} y = \frac{2 x}{y},$

we see that it is also a Bernoulli equation with P(x)=−3/(2x), Q(x)=2x, n=−1 $P (x) = - 3 / (2 x), Q (x) = 2 x, n = - 1$ , and 1−n=2 $1 - n = 2$ . Hence we substitute

v = y 2, y = v 1/2, and d y d x = d y d v d v d x = 1 2 v - 1/2 d v d x .

$\begin{array}{l} v = y^{2}, & y = v^{1/2}, & and & \frac{d y}{d x} = \frac{d y}{d v} \frac{d v}{d x} = \frac{1}{2} \end{array} v^{- 1/2} \frac{d v}{d x} .$

This gives

1 2 v - 1/2 d v d x - 3 2 x v 1/2 = 2 x v - 1/2 .

$\frac{1}{2} v^{- 1/2} \frac{d v}{d x} - \frac{3}{2 x} v^{1/2} = 2 x v^{- 1/2} .$

Then multiplication by 2v1/2 $2 v^{1/2}$ produces the linear equation

d v d x - 3 x v = 4 x

$\frac{d v}{d x} - \frac{3}{x} v = 4 x$

with integrating factor ρ=e∫(−3/x)dx=x−3 $ρ = e^{\int (- 3 / x) d x} = x^{- 3}$ . So we obtain

D x (x - 3 v) x - 3 v x - 3 y 2 y 2 = = = = 4 x 2; - 4 x + C; - 4 x + C; - 4 x 2 + C x 3 .

$\begin{array}{rcl} D_{x} (x^{- 3} v) & = & \frac{4}{x^{2}}; \\ x^{- 3} v & = & - \frac{4}{x} + C; \\ x^{- 3} y^{2} & = & - \frac{4}{x} + C; \\ y^{2} & = & - 4 x^{2} + C x^{3} . \end{array}$

Example 5

The equation

x d y d x + 6 y = 3 x y 4 / 3

$x \frac{d y}{d x} + 6 y = 3 x y^{4 / 3}$

is neither separable nor linear nor homogeneous, but it is a Bernoulli equation with n=43, 1−n=−13. $n = \frac{4}{3}, 1 - n = - \frac{1}{3} .$ The substitutions

v = y - 1/3, y = v - 3, and d y d x = d y d v d v d x = - 3 v - 4 d v d x

$v = y^{- 1/3}, y = v^{- 3}, and \frac{d y}{d x} = \frac{d y}{d v} \frac{d v}{d x} = - 3 v^{- 4} \frac{d v}{d x}$

transform it into

- 3 x v - 4 d v d x + 6 v - 3 = 3 x v - 4 .

$- 3 x v^{- 4} \frac{d v}{d x} + 6 v^{- 3} = 3 x v^{- 4} .$

Division by −3xv−4 $- 3 x v^{- 4}$ yields the linear equation

d v d x - 2 x v = - 1

$\frac{d v}{d x} - \frac{2}{x} v = - 1$

with integrating factor ρ=e∫(−2/x)dx=x−2 $ρ = e^{\int (- 2 / x) d x} = x^{- 2}$ . This gives

D x (x - 2 v) = - 1 x 2; x - 2 v = 1 x + C; v = x + C x 2;

$D_{x} (x^{- 2} v) = - \frac{1}{x^{2}}; x^{- 2} v = \frac{1}{x} + C; v = x + C x^{2};$

and finally,

y (x) = 1 ( x + C x 2 ) 3 .

$y (x) = \frac{1}{{(x + C x^{2})}^{3}} .$

Example 6

The equation

2 x e 2 y d y d x = 3 x 4 + e 2 y

$2 x e^{2 y} \frac{d y}{d x} = 3 x^{4} + e^{2 y}$ (11)

is neither separable, nor linear, nor homogeneous, nor is it a Bernoulli equation. But we observe that y appears only in the combinations e2y $e^{2 y}$ and Dx(e2y)=2e2yy' $D_{x} (e^{2 y}) = 2 e^{2 y} y ′$ . This prompts the substitution

v = e 2 y, d v d x = 2 e 2 y d y d x

$v = e^{2 y}, \frac{d v}{d x} = 2 e^{2 y} \frac{d y}{d x}$

that transforms Eq. (11) into the linear equation xv'(x)=3x4+v(x) $x v ′ (x) = 3 x^{4} + v (x)$ ; that is,

d v d x - 1 x v = 3 x 3 .

$\frac{d v}{d x} - \frac{1}{x} v = 3 x^{3} .$

After multiplying by the integrating factor ρ=1/x $ρ = 1 / x$ , we find that

1 x v = \int 3 x 2 d x = x 3 + C, so e 2 y = v = x 4 + C x,

$\begin{array}{l} \frac{1}{x} v = \int 3 x^{2} d x = x^{3} + C, & so & e^{2 y} = v = x^{4} + C x \end{array},$

and hence

y (x) = 1 2 ln ∣ ∣ x 4 + C x ∣ ∣ .

$y (x) = \frac{1}{2} \ln | x^{4} + C x | .$

Flight Trajectories

Suppose that an airplane departs from the point (a, 0) located due east of its intended destination—an airport located at the origin (0, 0). The plane travels with constant speed v0 $v_{0}$ relative to the wind, which is blowing due north with constant speed w. As indicated in Fig. 1.6.4, we assume that the plane’s pilot maintains its heading directly toward the origin.

FIGURE 1.6.4.

The airplane headed for the origin.

Figure 1.6.5 helps us derive the plane’s velocity components relative to the ground. They are

d x d t d y d t = = - v 0 cos θ = - v 0 x x 2 + y 2 - - - - - - \sqrt, - v 0 sin θ + w = - v 0 y x 2 + y 2 - - - - - - \sqrt + w .

$\begin{array}{rcl} \frac{d x}{d t} & = & - v_{0} \cos θ = - \frac{v_{0} x}{\sqrt{x^{2} + y^{2}}}, \\ \frac{d y}{d t} & = & - v_{0} \sin θ + w = - \frac{v_{0} y}{\sqrt{x^{2} + y^{2}}} + w . \end{array}$

Hence the trajectory y=f(x) $y = f (x)$ of the plane satisfies the differential equation

d y d x = d y / d t d x / d t = 1 v 0 x (v 0 y - w x 2 + y 2 - - - - - - \sqrt) .

$\frac{d y}{d x} = \frac{d y / d t}{d x / d t} = \frac{1}{v_{0} x} (v_{0} y - w \sqrt{x^{2} + y^{2}}) .$ (12)

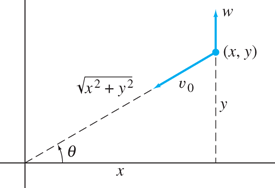
FIGURE 1.6.5.

The components of the velocity vector of the airplane.

If we set

$k = \frac{w}{v_{0}},$ (13)

the ratio of the windspeed to the plane’s airspeed, then Eq. (12) takes the homogeneous form

$\frac{d y}{d x} = \frac{y}{x} - k {[1 + {(\frac{y}{x})}^{2}]}^{1/2} .$ (14)

The substitution $y = x v, y ′ = v + x v ′$ then leads routinely to

$\int \frac{d v}{\sqrt{1 + v^{2}}} = - \int \frac{k}{x} d x .$ (15)

By trigonometric substitution, or by consulting a table for the integral on the left, we find that

$\ln (v + \sqrt{1 + v^{2}}) = - k \ln x + C,$ (16)

and the initial condition $v (a) = y (a) / a = 0$ yields

$C = k \ln a .$ (17)

As we ask you to show in Problem 68, the result of substituting (17) in Eq. (16) and then solving for v is

$v = \frac{1}{2} [{(\frac{x}{a})}^{- k} - {(\frac{x}{a})}^{k}] .$ (18)

Because $y = x v$ , we finally obtain

$y (x) = \frac{a}{2} [{(\frac{x}{a})}^{1 - k} - {(\frac{x}{a})}^{1 + k}]$ (19)

for the equation of the plane’s trajectory.

Note that only in the case $k < 1$ (that is, $w < v_{0}$ ) does the curve in Eq. (19) pass through the origin, so that the plane reaches its destination. If $w = v_{0}$ (so that $k = 1$ ), then Eq. (19) takes the form $y (x) = \frac{1}{2} a (1 - x^{2} / a^{2})$ , so the plane’s trajectory approaches the point (0, a/2) rather than (0, 0). The situation is even worse if $w > v_{0}$ (so $k > 1$ )-in this case it follows from Eq. (19) that $y \to + \infty$ as $x \to 0$ . The three cases are illustrated in Fig. 1.6.6.

FIGURE 1.6.6.

The three cases $w < v_{0}$ (plane velocity exceeds wind velocity), $w = v_{0}$ (equal velocities), and $w > v_{0}$ (wind is greater).

Example 7

Flight trajectory If $a = 200$ mi, $v_{0} = 500$ mi/h, and $w = 100$ mi/h, then $k = w / v_{0} = \frac{1}{5}$ , so the plane will succeed in reaching the airport at (0, 0). With these values, Eq. (19) yields

$y (x) = 100 [{(\frac{x}{200})}^{4/5} - {(\frac{x}{200})}^{6/5}] .$ (20)

Now suppose that we want to find the maximum amount by which the plane is blown off course during its trip. That is, what is the maximum value of y(x) for $0 ≦ x ≦ 200$ ?

Solution

Differentiation of the function in Eq. (20) yields

$\frac{d y}{d x} = \frac{1}{2} [\frac{4}{5} {(\frac{x}{200})}^{- 1/5} - \frac{6}{5} {(\frac{x}{200})}^{1/5}],$

and we readily solve the equation $y ′ (x) = 0$ to obtain ${(x / 200)}^{2/5} = \frac{2}{3}$ . Hence

$y_{\max} = 100 [{(\frac{2}{3})}^{2} - {(\frac{2}{3})}^{3}] = \frac{400}{27} \approx 14.81 .$

Thus the plane is blown almost 15 mi north at one point during its westward journey. (The graph of the function in Eq. (20) is the one used to construct Fig. 1.6.4. The vertical scale there is exaggerated by a factor of 4.)

Exact Differential Equations

We have seen that a general solution y(x) of a first-order differential equation is often defined implicitly by an equation of the form

$F (x, y (x)) = C,$ (21)

where C is a constant. On the other hand, given the identity in (21), we can recover the original differential equation by differentiating each side with respect to x. Provided that Eq. (21) implicitly defines y as a differentiable function of x, this gives the original differential equation in the form

$\frac{\partial F}{\partial x} + \frac{\partial F}{\partial y} \frac{d y}{d x} = 0;$

that is,

$M (x, y) + N (x, y) \frac{d y}{d x} = 0,$ (22)

where $M (x, y) = F_{x} (x, y)$ and $N (x, y) = F_{y} (x, y)$ .

It is sometimes convenient to rewrite Eq. (22) in the more symmetric form

$M (x, y) d x + N (x, y) d y = 0,$ (23)

called its differential form. The general first-order differential equation $y ′ = f (x, y)$ can be written in this form with $M = f (x, y)$ and $N \equiv - 1$ . The preceding discussion shows that, if there exists a function $F (x, y)$ such that

$\begin{array}{l} \frac{\partial F}{\partial x} = M & and & \frac{\partial F}{\partial y} = N, \end{array}$

then the equation

$F (x, y) = C$

implicitly defines a general solution of Eq. (23). In this case, Eq. (23) is called an exact differential equation—the differential

$d F = F_{x} d x + F_{y} d y$

of $F (x, y)$ is exactly $M d x + N d y$ .

Natural questions are these: How can we determine whether the differential equation in (23) is exact? And if it is exact, how can we find the function F such that $F_{x} = M$ and $F_{y} = N$ ? To answer the first question, let us recall that if the mixed second-order partial derivatives $F_{x y}$ and $F_{y x}$ are continuous on an open set in the xy-plane, then they are equal: $F_{x y} = F_{y x}$ . If Eq. (23) is exact and M and N have continuous partial derivatives, it then follows that

$\frac{\partial M}{\partial y} = F_{x y} = F_{y x} = \frac{\partial N}{\partial x} .$

Thus the equation

$\frac{\partial M}{\partial y} = \frac{\partial N}{\partial x}$ (24)

is a necessary condition that the differential equation $M d x + N d y = 0$ be exact. That is, if $M_{y} \neq N_{x}$ , then the differential equation in question is not exact, so we need not attempt to find a function $F (x, y)$ such that $F_{x} = M$ and $F_{y} = N$ —there is no such function.

Example 8

The differential equation

$y^{3} d x + 3 x y^{2} d y = 0$ (25)

is exact because we can immediately see that the function $F (x, y) = x y^{3}$ has the property that $F_{x} = y^{3}$ and $F_{y} = 3 {x y}^{2}$ . Thus a general solution of Eq. (25) is

$x y^{3} = C;$

if you prefer, $y (x) = k x^{- 1/3}$ .

But suppose that we divide each term of the differential equation in Example 8 by $y^{2}$ to obtain

$y d x + 3 x d y = 0 .$ (26)

This equation is not exact because, with $M = y$ and $N = 3 x,$ we have

$\frac{\partial M}{\partial y} = 1 \neq 3 = \frac{\partial N}{\partial x} .$

Hence the necessary condition in Eq. (24) is not satisfied.

We are confronted with a curious situation here. The differential equations in (25) and (26) are essentially equivalent, and they have exactly the same solutions, yet one is exact and the other is not. In brief, whether a given differential equation is exact or not is related to the precise form $M d x + N d y = 0$ in which it is written.

Theorem 1 tells us that (subject to differentiability conditions usually satisfied in practice) the necessary condition in (24) is also a sufficient condition for exactness. In other words, if $M_{y} = N_{x}$ , then the differential equation $M d x + N d y = 0$ is exact.

Proof:

We have seen already that it is necessary for Eq. (24) to hold if Eq. (23) is to be exact. To prove the converse, we must show that if Eq. (24) holds, then we can construct a function $F (x, y)$ such that $\partial F / \partial x = M$ and $\partial F / \partial y = N$ . Note first that, for any function g(y), the function

$F (x, y) = \int M (x, y) d x + g (y)$ (27)

satisfies the condition $\partial F / \partial x = M$ . (In Eq. (27), the notation $\int M (x, y) d x$ denotes an antiderivative of $M (x, y)$ with respect to x.) We plan to choose g(y) so that

$N = \frac{\partial F}{\partial y} = (\frac{\partial}{\partial y} \int M (x, y) d x) + g ′ (y)$

as well; that is, so that

$g ′ (y) = N - \frac{\partial}{\partial y} \int M (x, y) d x .$ (28)

To see that there is such a function of y, it suffices to show that the right-hand side in Eq. (28) is a function of y alone. We can then find g(y) by integrating with respect to y. Because the right-hand side in Eq. (28) is defined on a rectangle, and hence on an interval as a function of x, it suffices to show that its derivative with respect to x is identically zero. But

$\begin{array}{rcl} \frac{\partial}{\partial x} (N - \frac{\partial}{\partial y} \int M (x, y) d x) & = & \frac{\partial N}{\partial x} - \frac{\partial}{\partial x} \frac{\partial}{\partial y} \int M (x, y) d x \\ = & \frac{\partial N}{\partial x} - \frac{\partial}{\partial y} \frac{\partial}{\partial x} \int M (x, y) d x \\ = & \frac{\partial N}{\partial x} - \frac{\partial M}{\partial y} = 0 \end{array}$

by hypothesis. So we can, indeed, find the desired function g(y) by integrating Eq. (28). We substitute this result in Eq. (27) to obtain

$F (x, y) = \int M (x, y) d x + \int (N (x, y) - \frac{\partial}{\partial y} \int M (x, y) d x) d y$ (29)

as the desired function with $F_{x} = M$ and $F_{y} = N$ .

Instead of memorizing Eq. (29), it is usually better to solve an exact equation $M d x + N d y = 0$ by carrying out the process indicated by Eqs. (27) and (28). First we integrate $M (x, y)$ with respect to x and write

$F (x, y) = \int M (x, y) d x + g (y),$

thinking of the function g(y) as an “arbitrary constant of integration” as far as the variable x is concerned. Then we determine g(y) by imposing the condition that $\partial F / \partial y = N (x, y)$ . This yields a general solution in the implicit form $F (x, y) = C$ .

Example 9

Solve the differential equation

$(6 x y - y^{3}) d x + (4 y + 3 x^{2} - 3 x y^{2}) d y = 0 .$ (30)

Solution

Let $M (x, y) = 6 x y - y^{3}$ and $N (x, y) = 4 y + 3 x^{2} - 3 {x y}^{2}$ . The given equation is exact because

$\frac{\partial M}{\partial y} = 6 x - 3 y^{2} = \frac{\partial N}{\partial x} .$

Integrating $\partial F / \partial x = M (x, y)$ with respect to x, we get

$F (x, y) = \int (6 x y - y^{3}) d x = 3 x^{2} y - x y^{3} + g (y) .$

Then we differentiate with respect to y and set $\partial F / \partial y = N (x, y)$ . This yields

$\frac{\partial F}{\partial y} = 3 x^{2} - 3 x y^{2} + g ′ (y) = 4 y + 3 x^{2} - 3 x y^{2},$

and it follows that $g ′ (y) = 4 y$ . Hence $g (y) = 2 y^{2} + C_{1}$ , and thus

$F (x, y) = 3 x^{2} y - x y^{3} + 2 y^{2} + C_{1} .$

Therefore, a general solution of the differential equation is defined implicitly by the equation

$3 x^{2} y - x y^{3} + 2 y^{2} = C$ (31)

(we have absorbed the constant $C_{1}$ into the constant C).

Remark

Figure 1.6.7 shows a rather complicated structure of solution curves for the differential equation of Example 9. The solution satisfying a given initial condition $y (x_{0}) = y_{0}$ is defined implicitly by Eq. (31), with C determined by substituting $x = x_{0}$ and $y = y_{0}$ in the equation. For instance, the particular solution satisfying $y (0) = 1$ is defined implicitly by the equation $3 x^{2} y - x y^{3} + 2 y^{2} = 2$ . The other two special points in the figure—at (0, 0) and near $(0.75, 2.12)$ —are ones where both coefficient functions in Eq. (30) vanish, so the theorem of Section 1.3 does not guarantee a unique solution.

FIGURE 1.6.7.

Slope field and solution curves for the exact equation in Example 9.

Reducible Second-Order Equations

A second-order differential equation involves the second derivative of the unknown function y(x), and thus has the general form

$F (x, y, y^{′}, y^{″}) = 0 .$ (32)

If either the dependent variable y or the independent variable x is missing from a second-order equation, then it is easily reduced by a simple substitution to a first-order equation that may be solvable by the methods of this chapter.

Dependent variable y missing. If y is missing, then Eq. (32) takes the form

$F (x, y^{′}, y^{″}) = 0 .$ (33)

Then the substitution

$p = y^{′} = \frac{d y}{d x}, y^{″} = \frac{d p}{d x}$ (34)

results in the first-order differential equation

$F (x, p, p ′) = 0 .$

If we can solve this equation for a general solution $p (x, C_{1})$ involving an arbitrary constant $C_{1}$ , then we need only write

$x (x) = \int y ′ (x) d x = \int p (x, C_{1}) d x + C_{2}$

to get a solution of Eq. (33) that involves two arbitrary constants $C_{1}$ and $C_{2}$ (as is to be expected in the case of a second-order differential equation).

Example 10

Solve the equation $x y^{″} + 2 y^{′} = 6 x$ in which the dependent variable y is missing.

Solution

The substitution defined in (34) gives the first-order equation

$\begin{array}{l} x \frac{d p}{d x} + 2 p = 6 x; & that is, & \frac{d p}{d x} + \frac{2}{x} p = 6 . \end{array}$

Observing that the equation on the right here is linear, we multiply by its integrating factor $ρ = \exp (\int (2 / x) d x) = e^{2 \ln x} = x^{2}$ and get

$\begin{array}{rcl} D_{x} (x^{2} p) & = & 6 x^{2}, \\ x^{2} p & = & 2 x^{3} + C_{1}, \\ p & = & \frac{d y}{d x} = 2 x + \frac{C_{1}}{x^{2}} . \end{array}$

A final integration with respect to x yields the general solution

$y (x) = x^{2} - \frac{C_{1}}{x} + C_{2}$

of the second-order equation $x y ″ + 2 y ′ = 6 x$ . Solution curves with $C_{1} = 0$ but $C_{2} \neq 0$ are simply vertical translates of the parabola $y = x^{2}$ (for which $C_{1} = C_{2} = 0$ ). Figure 1.6.8 shows this parabola and some typical solution curves with $C_{2} = 0$ but $C_{1} \neq 0$ . Solution curves with $C_{1}$ and $C_{2}$ both nonzero are vertical translates of those (other than the parabola) shown in Fig. 1.6.8.

FIGURE 1.6.8.

Solution curves of the form $y (x) = x^{2} - \frac{C_{1}}{x}$ for $C_{1} = 0, \pm 3, \pm 10, \pm 20, \pm 35, \pm 60, \pm 100$ .

Independent variable x missing. If x is missing, then Eq. (32) takes the form

$F (y, y^{′}, y^{″}) = 0 .$ (35)

Then the substitution

$p = y^{′} = \frac{d y}{d x}, y^{″} = \frac{d p}{d x} = \frac{d p}{d y} \frac{d y}{d x} = p \frac{d p}{d y}$ (36)

results in the first-order differential equation

$F (y, p, p \frac{d p}{d y}) = 0$

for p as a function of y. If we can solve this equation for a general solution $p (y, C_{1})$ involving an arbitrary constant $C_{1}$ , then (assuming that $y^{′} \neq 0$ ) we need only write

$x (y) = \int \frac{d x}{d y} d y = \int \frac{1}{d y / d x} d y = \int \frac{1}{p} d y = \int \frac{d y}{p (y, C_{1})} + C_{2} .$

If the final integral $P = \int (1 / p) d y$ can be evaluated, the result is an implicit solution $x (y) = P (y, C_{1}) + C_{2}$ of our second-order differential equation.

Example 11

Solve the equation $y y^{″} = {(y^{′})}^{2}$ in which the independent variable x is missing.

Solution

We assume temporarily that y and $y^{′}$ are both nonnegative, and then point out at the end that this restriction is unnecessary. The substitution defined in (36) gives the first-order equation

$y p \frac{d p}{d y} = p^{2} .$

Then separation of variables gives

$\begin{array}{rcl} \int \frac{d p}{p} & = & \int \frac{d y}{y}, \\ \ln p & = & \ln y + C (because y > 0 and p = y^{′} > 0), \\ p & = & C_{1} y \end{array}$

where $C_{1} = e^{C}$ . Hence

$\begin{array}{rcl} \frac{d x}{d y} & = & \frac{1}{p} = \frac{1}{C_{1} y}, \\ C_{1} x & = & \int \frac{d y}{y} = \ln y + C_{2} . \end{array}$

The resulting general solution of the second-order equation $y y^{″} = {(y^{′})}^{2}$ is

$y (x) = \exp (C_{1} x - C_{2}) = A e^{B x},$

where $A = e^{- C_{2}}$ and $B = C_{1}$ . Despite our temporary assumptions, which imply that the constants A and B are both positive, we readily verify that $y (x) = {A e}^{B x}$ satisfies $y y^{″} = {(y^{′})}^{2}$ for all real values of A and B. With $B = 0$ and different values of A, we get all horizontal lines in the plane as solution curves. The upper half of Fig. 1.6.9 shows the solution curves obtained with $A = 1$ (for instance) and different positive values of B. With $A = - 1$ these solution curves are reflected in the x-axis, and with negative values of B they are reflected in the y-axis. In particular, we see that we get solutions of $y y^{″} = {(y^{′})}^{2}$ , allowing both positive and negative possibilities for both y and $y ′$ .

FIGURE 1.6.9.

The solution curves $y = {A e}^{B x}$ with $B = 0$ and $A = 0, \pm 1$ are the horizontal lines $y = 0, \pm 1$ . The exponential curves with $B > 0$ and $A = \pm 1$ are in color, those with $B < 0$ and $A = \pm 1$ are black.

1.6 Problems

Find general solutions of the differential equations in Problems 1 through 30. Primes denote derivatives with respect to x throughout.

$(x + y) y^{′} = x - y$
$2 x y y^{′} = x^{2} + 2 y^{2}$
$x y^{′} = y + 2 \sqrt{x y}$
$(x - y) y^{′} = x + y$
$x (x + y) y^{′} = y (x - y)$
$(x + 2 y) y^{′} = y$
$x y^{2} y^{′} = x^{3} + y^{3}$
$x^{2} y ′ = x y + x^{2} e^{y / x}$
$x^{2} y ′ = x y + y^{2}$
$x y y^{′} = x^{2} + 3 y^{2}$
$(x^{2} - y^{2}) y^{′} = 2 x y$
$x y y^{′} = y^{2} + x \sqrt{4 x^{2} + y^{2}}$
$x y^{′} = y + \sqrt{x^{2} + y^{2}}$
$y y^{′} + x = \sqrt{x^{2} + y^{2}}$
$x (x + y) y^{′} + y (3 x + y) = 0$
$y^{′} = \sqrt{x + y + 1}$
$y^{′} = {(4 x + y)}^{2}$
$(x + y) y^{′} = 1$
$x^{2} y^{′} + 2 x y = 5 y^{3}$
$y^{2} y^{′} + 2 x y^{3} = 6 x$
$y^{′} = y + y^{3}$
$x^{2} y^{′} + 2 x y = 5 y^{4}$
$x y^{′} + 6 y = 3 x y^{4/3}$
$2 x y^{′} + y^{3} e^{- 2 x} = 2 x y$
$y^{2} (x y^{′} + y) {(1 + x^{4})}^{1/2} = x$
$3 y^{2} y^{′} + y^{3} = e^{- x}$
$3 {x y}^{2} y ′ = 3 x^{4} + y^{3}$
$x e^{y} y ′ = 2 (e^{y} + x^{3} e^{2 x})$
$(2 x \sin y \cos y) y^{′} = 4 x^{2} + \sin^{2} y$
$(x + e^{y}) y^{′} = x e^{- y} - 1$

In Problems 31 through 42, verify that the given differential equation is exact; then solve it.

$(2 x + 3 y) d x + (3 x + 2 y) d y = 0$
$(4 x - y) d x + (6 y - x) d y = 0$
$(3 x^{2} + 2 y^{2}) d x + (4 x y + 6 y^{2}) d y = 0$
$(2 {x y}^{2} + 3 x^{2}) d x + (2 x^{2} y + 4 y^{3}) d y = 0$
$(x^{3} + \frac{y}{x}) d x + (y^{2} + \ln x) d y = 0$
$(1 + y e^{x y}) d x + (2 y + x e^{x y}) d y = 0$
$(\cos x + \ln y) d x + (\frac{x}{y} + e^{y}) d y = 0$
$(x + \tan^{- 1} y) d x + \frac{x + y}{1 + y^{2}} d y = 0$
$(3 x^{2} y^{3} + y^{4}) d x + (3 x^{3} y^{2} + y^{4} + 4 {x y}^{3}) d y = 0$
$(e^{x} \sin y + \tan y) d x + (e^{x} \cos y + x \sec^{2} y) d y = 0$
$(\frac{2 x}{y} - \frac{3 y^{2}}{x^{4}}) d x + (\frac{2 y}{x^{3}} - \frac{x^{2}}{y^{2}} + \frac{1}{\sqrt{y}}) d y = 0$
$\frac{2 x^{5/2} - 3 y^{5/3}}{2 x^{5/2} y^{2/3}} d x + \frac{3 y^{5/3} - 2 x^{5/2}}{3 x^{3/2} y^{5/3}} d y = 0$

Find a general solution of each reducible second-order differential equation in Problems 43–54. Assume x, y and/or $y ′$ positive where helpful (as in Example 11).

$x y^{″} = y^{′}$
$y y^{″} + {(y^{′})}^{2} = 0$
$y^{″} + 4 y = 0$
$x y^{″} + y^{′} = 4 x$
$y^{″} = {(y^{′})}^{2}$
$x^{2} y^{″} + 3 x y^{′} = 2$
$y y^{″} + {(y^{′})}^{2} = y y^{′}$
$y^{″} = {(x + y^{′})}^{2}$
$y^{″} = 2 y {(y^{′})}^{3}$
$y^{3} y^{″} = 1$
$y^{″} = 2 y y^{′}$
$y y^{″} = 3 {(y^{′})}^{2}$
Show that the substitution $v = a x + b y + c$ transforms the differential equation $d y / d x = F (a x + b y + c)$ into a separable equation.
Suppose that $n \neq 0$ and $n \neq 1$ . Show that the substitution $v = y^{1 - n}$ transforms the Bernoulli equation $d y / d x + P (x) y = Q (x) y^{n}$ into the linear equation

$\frac{d v}{d x} + (1 - n) P (x) v (x) = (1 - n) Q (x) .$
Show that the substitution $v = \ln y$ transforms the differential equation $d y / d x + P (x) y = Q (x) (y \ln y)$ into the linear equation $d v / d x + P (x) = Q (x) v (x)$ .
Use the idea in Problem 57 to solve the equation

$x \frac{d y}{d x} - 4 x^{2} y + 2 y \ln y = 0 .$
Solve the differential equation

$\frac{d y}{d x} = \frac{x - y - 1}{x + y + 3}$

by finding h and k so that the substitutions $x = u + h, y = v + k$ transform it into the homogeneous equation

$\frac{d v}{d u} = \frac{u - v}{u + v} .$
Use the method in Problem 59 to solve the differential equation

$\frac{d y}{d x} = \frac{2 x - x + 7}{4 x - 3 y - 18} .$
Make an appropriate substitution to find a solution of the equation $d y / d x = \sin (x - y)$ . Does this general solution contain the linear solution $y (x) = x - π / 2$ that is readily verified by substitution in the differential equation?
Show that the solution curves of the differential equation

$\frac{d y}{d x} = - \frac{y (2 x^{3} - y^{3})}{x (2 y^{3} - x^{3})}$

are of the form $x^{3} + y^{3} = C x y$ .
The equation $d y / d x = A (x) y^{2} + B (x) y + C (x)$ is called a Riccati equation. Suppose that one particular solution $y_{1} (x)$ of this equation is known. Show that the substitution

$y = y_{1} + \frac{1}{v}$

transforms the Riccati equation into the linear equation

$\frac{d v}{d x} + (B + 2 A y_{1}) v = - A .$

Use the method of Problem 63 to solve the equations in Problems 64 and 65, given that $y_{1} (x) = x$ is a solution of each.

$\frac{d y}{d x} + y^{2} = 1 + x^{2}$
$\frac{d y}{d x} + 2 x y = 1 + x^{2} + y^{2}$
An equation of the form

$y = x y^{′} + g (y^{′})$ (37)

is called a Clairaut equation. Show that the one-parameter family of straight lines described by

$y (x) = C x + g (C)$ (38)

is a general solution of Eq. (37).
Consider the Clairaut equation

$y = x y^{′} - \frac{1}{4} {(y^{′})}^{2}$

for which $g (y^{′}) = - \frac{1}{4} {(y^{′})}^{2}$ in Eq. (37). Show that the line

$y = C x - \frac{1}{4} C^{2}$

is tangent to the parabola $y = x^{2}$ at the point $(\frac{1}{2} C, \frac{1}{4} C^{2}) .$

Explain why this implies that $y = x^{2}$ g is a singular solution of the given Clairaut equation. This singular solution and the one-parameter family of straight line solutions are illustrated in Fig. 1.6.10.

FIGURE 1.6.10.

Solutions of the Clairaut equation of Problem 67. The “typical” straight line with equation $y = C x - \frac{1}{4} C^{2}$ is tangent to the parabola at the point $(\frac{1}{2} C, \frac{1}{4} C^{2}) .$
Derive Eq. (18) in this section from Eqs. (16) and (17).
Flight trajectory In the situation of Example 7, suppose that $a = 100 mi, v_{0} = 400 mi/h,$ and $w = 40 mi/h .$ Now how far northward does the wind blow the airplane?
Flight trajectory As in the text discussion, suppose that an airplane maintains a heading toward an airport at the origin. If $v_{0} = 500 mi/h$ and $w = 50 mi/h$ (with the wind blowing due north), and the plane begins at the point (200, 150), show that its trajectory is described by

$y + \sqrt{x^{2} + y^{2}} = 2 {(200 x^{9})}^{1/10} .$
River crossing A river 100 ft wide is flowing north at w feet per second. A dog starts at (100, 0) and swims at $v_{0} = 4 ft/s$ , always heading toward a tree at (0, 0) on the west bank directly across from the dog’s starting point. (a) If $w = 2 ft/s$ , show that the dog reaches the tree. (b) If $w = 4 ft/s$ , show that the dog reaches instead the point on the west bank 50 ft north of the tree. (c) If $w = 6 ft/s$ , show that the dog never reaches the west bank.
In the calculus of plane curves, one learns that the curvature $κ$ of the curve $y = y (x)$ at the point (x, y) is given by

$κ = \frac{| y^{″} (x) |}{{[1 + y^{′} {(x)}^{2}]}^{3/2}},$

and that the curvature of a circle of radius r is $κ = 1 / r$ . [See Example 3 in Section 11.6 of Edwards and Penney, Calculus: Early Transcendentals, 7th edition, Hoboken, NJ: Pearson, 2008.] Conversely, substitute $ρ = y ′$ to derive a general solution of the second-order differential equation

$r y^{″} = {[1 + {(y^{′})}^{2}]}^{3/2}$

(with r constant) in the form

${(x - a)}^{2} + {(y - b)}^{2} = r^{2} .$

Thus a circle of radius r (or a part thereof) is the only plane curve with constant curvature $1 / r$ .

1.6 Application Computer Algebra Solutions

Computer algebra systems typically include commands for the “automatic” solution of differential equations. But two different such systems often give different results whose equivalence is not clear, and a single system may give the solution in an overly complicated form. Consequently, computer algebra solutions of differential equations often require considerable “processing” or simplification by a human user in order to yield concrete and applicable information. Here we illustrate these issues using the interesting differential equation

$\frac{d y}{d x} = \sin (x - y)$ (1)

that appeared in the Section 1.3 Application. The Maple command

dsolve( D(y)(x) = sin(x - y(x)), y(x));

yields the simple and attractive result

$y (x) = x - 2 \tan^{- 1} (\frac{x - 2 - C 1}{x - C 1})$ (2)

that was cited there. But the supposedly equivalent Mathematica command

DSolve[ y′[x] == Sin[x y[x]], y[x], x]

and the $Wolfram|Alpha query$

Y′ = sin(x - y)

both yield considerably more complicated results from which—with a fair amount of effort in simplification—one can extract the quite different looking solution

$y (x) = 2 \cos^{- 1} (\frac{2 \cos \frac{x}{2} + (x - c) (\cos \frac{x}{2} + \sin \frac{x}{2})}{\sqrt{2 + 2 {(x - c + 1)}^{2}}}) .$ (3)

This apparent disparity is not unusual; different symbolic algebra systems, or even different versions of the same system, often yield different forms of a solution of the same differential equation. As an alternative to attempted reconciliation of such seemingly disparate results as in Eqs. (2) and (3), a common tactic is simplification of the differential equation before submitting it to a computer algebra system.

Exercise 1: Show that the plausible substitution $v = x - y$ in Eq. (1) yields the separable equation

$\frac{d v}{d x} = 1 - \sin v .$ (4)

Now the Maple command int(1/(1 - sin(v)), v) yields

$\int \frac{d v}{1 - \sin v} = \frac{2}{1 - \tan \frac{v}{2}}$ (5)

(omitting the constant of integration, as symbolic computer algebra systems often do).

Exercise 2: Use simple algebra to deduce from Eq. (5) the integral formula

$\int \frac{d v}{1 - \sin v} = \frac{1 + \tan \frac{v}{2}}{1 - \tan \frac{v}{2}} + C .$ (6)

Exercise 3: Deduce from (6) that Eq. (4) has the general solution

$v (x) = 2 \tan^{- 1} (\frac{x - 1 + C}{x + 1 + C}),$

and hence that Eq. (1) has the general solution

$y (x) = x - 2 \tan^{- 1} (\frac{x - 1 + C}{x + 1 + C}) .$ (7)

Exercise 4: Finally, reconcile the forms in Eq. (2) and Eq. (7). What is the relation between the constants C and $C 1$ ?

Exercise 5: Show that the integral in Eq. (5) yields immediately the graphing calculator implicit solution shown in Fig. 1.6.11.

Investigation: For your own personal differential equation, let p and q be two distinct nonzero digits in your student ID number, and consider the differential equation

FIGURE 1.6.11.

Implicit solution of $y ′ = \sin (x - y)$ generated by a TI-Nspire CX CAS.

$\frac{d y}{d x} = \frac{1}{p} \cos (x - q y) .$ (8)

Find a symbolic general solution using a computer algebra system and/or some combination of the techniques listed in this project.
Determine the symbolic particular solution corresponding to several typical initial conditions of the form $y (x_{0}) = y_{0}$ .
Determine the possible values of a and b such that the straight line $y = a x + b$ is a solution curve of Eq. (8).
Plot a direction field and some typical solution curves. Can you make a connection between the symbolic solution and your (linear and nonlinear) solution curves?

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 1.6 Substitution Methods and Exact Equations

Create new playlist

Sign In

Sign Up

Table of Contents for
1.6 Substitution Methods and Exact Equations