Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

1.2 Integrals as General and Particular Solutions

The first-order equation $d y / d x = f (x, y)$ $d y / d x = f (x, y)$ takes an especially simple form if the right-hand-side function f does not actually involve the dependent variable y, so

\frac{d y}{d x} = f (x) .

$\frac{d y}{d x} = f (x) .$ (1)

In this special case we need only integrate both sides of Eq. (1) to obtain

y (x) = \int f (x) d x + C .

$y (x) = \int f (x) d x + C .$ (2)

This is a general solution of Eq. (1), meaning that it involves an arbitrary constant C, and for every choice of C it is a solution of the differential equation in (1). If G(x) is a particular antiderivative of f—that is, if $G ′ (x) \equiv f (x)$ $G ′ (x) \equiv f (x)$ —then

y (x) = G (x) + C .

$y (x) = G (x) + C .$ (3)

FIGURE 1.2.1.

Graphs of $y = \frac{1}{4} x^{2} + C$ $y = \frac{1}{4} x^{2} + C$ for various values of `C`.

FIGURE 1.2.2.

Graphs of $y = \sin x + C$ $y = \sin x + C$ for various values of `C`.

The graphs of any two such solutions $y_{1} (x) = G (x) + C_{1}$ $y_{1} (x) = G (x) + C_{1}$ and $y_{2} (x) = G (x) + C_{2}$ $y_{2} (x) = G (x) + C_{2}$ on the same interval I are “parallel” in the sense illustrated by Figs. 1.2.1 and 1.2.2. There we see that the constant C is geometrically the vertical distance between the two curves $y (x) = G (x)$ $y (x) = G (x)$ and $y (x) = G (x) + C$ $y (x) = G (x) + C$ .

To satisfy an initial condition $y (x_{0}) = y_{0}$ $y (x_{0}) = y_{0}$ , we need only substitute $x = x_{0}$ $x = x_{0}$ and $y = y_{0}$ $y = y_{0}$ into Eq. (3) to obtain $y_{0} = G (x_{0}) + C$ $y_{0} = G (x_{0}) + C$ , so that $C = y_{0} - G (x_{0})$ $C = y_{0} - G (x_{0})$ . With this choice of C, we obtain the particular solution of Eq. (1) satisfying the initial value problem

\begin{array}{l} \frac{d y}{d x} = f (x), & y (x_{0}) = y_{0} . \end{array}

$\begin{array}{l} \frac{d y}{d x} = f (x), & y (x_{0}) = y_{0} . \end{array}$

We will see that this is the typical pattern for solutions of first-order differential equations. Ordinarily, we will first find a general solution involving an arbitrary constant C. We can then attempt to obtain, by appropriate choice of C, a particular solution satisfying a given initial condition $y (x_{0}) = y_{0}$ $y (x_{0}) = y_{0}$ .

Remark

As the term is used in the previous paragraph, a general solution of a first-order differential equation is simply a one-parameter family of solutions. A natural question is whether a given general solution contains every particular solution of the differential equation. When this is known to be true, we call it the general solution of the differential equation. For example, because any two antiderivatives of the same function f(x) can differ only by a constant, it follows that every solution of Eq. (1) is of the form in (2). Thus Eq. (2) serves to define the general solution of (1).

Example 1

Solve the initial value problem

\begin{array}{l} \frac{d y}{d x} = 2 x + 3, & y (1) = 2 . \end{array}

$\begin{array}{l} \frac{d y}{d x} = 2 x + 3, & y (1) = 2 . \end{array}$

Solution

Integration of both sides of the differential equation as in Eq. (2) immediately yields the general solution

y (x) = \int (2 x + 3) d x = x^{2} + 3 x + C .

$y (x) = \int (2 x + 3) d x = x^{2} + 3 x + C .$

Figure 1.2.3 shows the graph $y = x^{2} + 3 x + C$ $y = x^{2} + 3 x + C$ for various values of C. The particular solution we seek corresponds to the curve that passes through the point (1, 2), thereby satisfying the initial condition

y (1) = {(1)}^{2} + 3 \cdot (1) + C = 2 .

$y (1) = {(1)}^{2} + 3 \cdot (1) + C = 2 .$

It follows that $C = - 2$ $C = - 2$ , so the desired particular solution is

y (x) = x^{2} + 3 x - 2 .

$y (x) = x^{2} + 3 x - 2 .$

Second-order equations. The observation that the special first-order equation $d y / d x = f (x)$ $d y / d x = f (x)$ is readily solvable (provided that an antiderivative of f can be found) extends to second-order differential equations of the special form

\frac{d^{2} y}{d x^{2}} = g (x),

$\frac{d^{2} y}{d x^{2}} = g (x),$ (4)

FIGURE 1.2.3.

Solution curves for the differential equation in Example 1.

in which the function g on the right-hand side involves neither the dependent variable y nor its derivative $d y / d x$ $d y / d x$ . We simply integrate once to obtain

\frac{d y}{d x} = \int y^{″} (x) d x = \int g (x) d x = G (x) + C_{1},

$\frac{d y}{d x} = \int y^{″} (x) d x = \int g (x) d x = G (x) + C_{1},$

where G is an antiderivative of g and $C_{1}$ $C_{1}$ is an arbitrary constant. Then another integration yields

y (x) = \int y^{′} (x) d x = \int [G (x) + C_{1}] d x = \int G (x) d x + C_{1} x + C_{2},

$y (x) = \int y^{′} (x) d x = \int [G (x) + C_{1}] d x = \int G (x) d x + C_{1} x + C_{2},$

where $C_{2}$ $C_{2}$ is a second arbitrary constant. In effect, the second-order differential equation in (4) is one that can be solved by solving successively the first-order equations

\begin{array}{l} \frac{d v}{d x} = g (x) & and & \frac{d y}{d x} = υ (x) . \end{array}

$\begin{array}{l} \frac{d v}{d x} = g (x) & and & \frac{d y}{d x} = υ (x) . \end{array}$

Velocity and Acceleration

Direct integration is sufficient to allow us to solve a number of important problems concerning the motion of a particle (or mass point) in terms of the forces acting on it. The motion of a particle along a straight line (the x-axis) is described by its position function

x = f (t)

$x = f (t)$ (5)

giving its x-coordinate at time t. The velocity of the particle is defined to be

\begin{array}{l} υ (t) = f^{′} (t); & that is, & υ = \frac{d x}{d t} . \end{array}

$\begin{array}{l} υ (t) = f^{′} (t); & that is, & υ = \frac{d x}{d t} . \end{array}$ (6)

Its acceleration a(t) is $a (t) = v ′ (t) = x ″ (t)$ $a (t) = v ′ (t) = x ″ (t)$ ; in Leibniz notation,

a = \frac{d υ}{d t} = \frac{d^{2} x}{d t^{2}} .

$a = \frac{d υ}{d t} = \frac{d^{2} x}{d t^{2}} .$ (7)

Equation (6) is sometimes applied either in the indefinite integral form $x (t) = \int v (t) d t$ $x (t) = \int v (t) d t$ or in the definite integral form

x (t) = x (t_{0}) + \int_{t_{0}}^{t} υ (s) d s,

$x (t) = x (t_{0}) + \int_{t_{0}}^{t} υ (s) d s,$

which you should recognize as a statement of the fundamental theorem of calculus (precisely because $d x / d t = v$ $d x / d t = v$ ).

Newton’s second law of motion says that if a force F(t) acts on the particle and is directed along its line of motion, then

\begin{array}{l} m a (t) = F (t); & that is, & F = m a, \end{array}

$\begin{array}{l} m a (t) = F (t); & that is, & F = m a, \end{array}$ (8)

where m is the mass of the particle. If the force F is known, then the equation $x ″ (t) = F (t) / m$ $x ″ (t) = F (t) / m$ can be integrated twice to find the position function x(t) in terms of two constants of integration. These two arbitrary constants are frequently determined by the initial position $x_{0} = x (0)$ $x_{0} = x (0)$ and the initial velocity $v_{0} = v (0)$ $v_{0} = v (0)$ of the particle.

Constant acceleration. For instance, suppose that the force F, and therefore the acceleration $a = F / m$ $a = F / m$ , are constant. Then we begin with the equation

\begin{array}{l} \frac{d υ}{d t} = a & (a is a constant) \end{array}

$\begin{array}{l} \frac{d υ}{d t} = a & (a is a constant) \end{array}$ (9)

and integrate both sides to obtain

υ (t) = \int a d t = a t + C_{1} .

$υ (t) = \int a d t = a t + C_{1} .$

We know that $v = v_{0}$ $v = v_{0}$ when $t = 0$ $t = 0$ , and substitution of this information into the preceding equation yields the fact that $C_{1} = v_{0}$ $C_{1} = v_{0}$ . So

v (t) = \frac{d x}{d t} = a t + υ_{0} .

$v (t) = \frac{d x}{d t} = a t + υ_{0} .$ (10)

A second integration gives

x (t) = \int υ (t) d t = \int (a t + υ_{0}) d t = \frac{1}{2} a t^{2} + υ_{0} t + C_{2},

$x (t) = \int υ (t) d t = \int (a t + υ_{0}) d t = \frac{1}{2} a t^{2} + υ_{0} t + C_{2},$

and the substitution $t = 0, x = x_{0}$ $t = 0, x = x_{0}$ gives $C_{2} = x_{0.}$ $C_{2} = x_{0.}$ Therefore,

x (t) = \frac{1}{2} a t^{2} + υ_{0} t + x_{0} .

$x (t) = \frac{1}{2} a t^{2} + υ_{0} t + x_{0} .$ (11)

Thus, with Eq. (10) we can find the velocity, and with Eq. (11) the position, of the particle at any time t in terms of its constant acceleration a, its initial velocity $v_{0}$ $v_{0}$ , and its initial position $x_{0}$ $x_{0}$ .

Example 2

Lunar lander A lunar lander is falling freely toward the surface of the moon at a speed of 450 meters per second (m/s). Its retrorockets, when fired, provide a constant deceleration of 2.5 meters per second per second $({m/s}^{2})$ $({m/s}^{2})$ (the gravitational acceleration produced by the moon is assumed to be included in the given deceleration). At what height above the lunar surface should the retrorockets be activated to ensure a “soft touchdown” $(v = 0$ $(v = 0$ at impact)?

Solution

We denote by x(t) the height of the lunar lander above the surface, as indicated in Fig. 1.2.4. We let $t = 0$ $t = 0$ denote the time at which the retrorockets should be fired. Then $v_{0} = - 450$ $v_{0} = - 450$ (m/s, negative because the height x(t) is decreasing), and $a = + 2.5$ $a = + 2.5$ , because an upward thrust increases the velocity v (although it decreases the speed $| v |$ $| v |$ ). Then Eqs. (10) and (11) become

FIGURE 1.2.4.

The lunar lander of Example 2.

υ (t) = 2.5 t - 450

$υ (t) = 2.5 t - 450$ (12)

and

x (t) = 1.25 t^{2} - 450 t + x_{0},

$x (t) = 1.25 t^{2} - 450 t + x_{0},$ (13)

where $x_{0}$ $x_{0}$ is the height of the lander above the lunar surface at the time $t = 0$ $t = 0$ when the retrorockets should be activated.

From Eq. (12) we see that $v = 0$ $v = 0$ (soft touchdown) occurs when $t = 450/2.5 = 180$ $t = 450/2.5 = 180$ s(that is, 3 minutes); then substitution of $t = 180, x = 0$ $t = 180, x = 0$ into Eq. (13) yields

x_{0} = 0 - (1.25) {(180)}^{2} + 450 (180) = 40, 500

$x_{0} = 0 - (1.25) {(180)}^{2} + 450 (180) = 40, 500$

meters—that is, $x_{0} = 40.5 km \approx 25 \frac{1}{6} miles.$ $x_{0} = 40.5 km \approx 25 \frac{1}{6} miles.$ Thus the retrorockets should be activated when the lunar lander is 40.5 kilometers above the surface of the moon, and it will touch down softly on the lunar surface after 3 minutes of decelerating descent.

Physical Units

Numerical work requires units for the measurement of physical quantities such as distance and time. We sometimes use ad hoc units—such as distance in miles or kilometers and time in hours—in special situations (such as in a problem involving an auto trip). However, the foot-pound-second (fps) and meter-kilogram-second (mks) unit systems are used more generally in scientific and engineering problems. In fact, fps units are commonly used only in the United States (and a few other countries), while mks units constitute the standard international system of scientific units.

	fps units	mks units
Force	pound (lb)	newton (N)
Mass	slug	kilogram (kg)
Distance	foot (ft)	meter (m)
Time	second (s)	second (s)
`g`	${32 ft/s}^{2}$ ${32 ft/s}^{2}$	${9.8 m/s}^{2}$ ${9.8 m/s}^{2}$

The last line of this table gives values for the gravitational acceleration g at the surface of the earth. Although these approximate values will suffice for most examples and problems, more precise values are $9.7805 {m/s}^{2}$ $9.7805 {m/s}^{2}$ and $32.088 {ft/s}^{2}$ $32.088 {ft/s}^{2}$ (at sea level at the equator).

Both systems are compatible with Newton’s second law $F = m a$ $F = m a$ . Thus 1 N is (by definition) the force required to impart an acceleration of $1 {m/s}^{2}$ $1 {m/s}^{2}$ to a mass of 1 kg. Similarly, 1 slug is (by definition) the mass that experiences an acceleration of $1 {ft/s}^{2}$ $1 {ft/s}^{2}$ under a force of 1 lb. (We will use mks units in all problems requiring mass units and thus will rarely need slugs to measure mass.)

Inches and centimeters (as well as miles and kilometers) also are commonly used in describing distances. For conversions between fps and mks units it helps to remember that

\begin{array}{l} 1 in . = 2.54 cm (exactly) & and & 1 lb \approx 4.448 N . \end{array}

$\begin{array}{l} 1 in . = 2.54 cm (exactly) & and & 1 lb \approx 4.448 N . \end{array}$

For instance,

1 ft = 12 in . \times 2.54 \frac{cm}{in .} = 30.48 cm,

$1 ft = 12 in . \times 2.54 \frac{cm}{in .} = 30.48 cm,$

and it follows that

1 mi = 5280 ft \times 30.48 \frac{cm}{ft} = 160934.4 cm \approx 1.609 km .

$1 mi = 5280 ft \times 30.48 \frac{cm}{ft} = 160934.4 cm \approx 1.609 km .$

Thus a posted U.S. speed limit of 50 mi/h means that—in international terms—the legal speed limit is about $50 \times 1.609 \approx 80.45 km/h$ $50 \times 1.609 \approx 80.45 km/h$ .

Vertical Motion with Gravitational Acceleration

The weight W of a body is the force exerted on the body by gravity. Substitution of $a = g$ $a = g$ and $F = W$ $F = W$ in Newton’s second law $F = m a$ $F = m a$ gives

W = m g

$W = m g$ (14)

for the weight W of the mass m at the surface of the earth (where $g \approx 32 {ft/s}^{2} \approx 9.8 {m/s}^{2}$ $g \approx 32 {ft/s}^{2} \approx 9.8 {m/s}^{2}$ ). For instance, a mass of $m = 20 kg$ $m = 20 kg$ has a weight of $W = (20 kg) ({9.8 m/s}^{2}) = 196 N.$ $W = (20 kg) ({9.8 m/s}^{2}) = 196 N.$ Similarly, a mass m weighing 100 pounds has mks weight

W = (100 lb) (4.448 N / lb) = 444.8 N,

$W = (100 lb) (4.448 N / lb) = 444.8 N,$

so its mass is

m = \frac{W}{g} = \frac{444.8 N}{9.8 {m/s}^{2}} \approx 45.4 kg .

$m = \frac{W}{g} = \frac{444.8 N}{9.8 {m/s}^{2}} \approx 45.4 kg .$

To discuss vertical motion it is natural to choose the y-axis as the coordinate system for position, frequently with $y = 0$ $y = 0$ corresponding to “ground level.” If we choose the upward direction as the positive direction, then the effect of gravity on a vertically moving body is to decrease its height and also to decrease its velocity $v = d y / d t$ $v = d y / d t$ . Consequently, if we ignore air resistance, then the acceleration $a = d v / d t$ $a = d v / d t$ of the body is given by

\frac{d υ}{d t} = - g .

$\frac{d υ}{d t} = - g .$ (15)

This acceleration equation provides a starting point in many problems involving vertical motion. Successive integrations (as in Eqs. (10) and (11)) yield the velocity and height formulas

υ (t) = - g t + υ_{0}

$υ (t) = - g t + υ_{0}$ (16)

and

y (t) = - \frac{1}{2} g t^{2} + υ_{0} t + y_{0} .

$y (t) = - \frac{1}{2} g t^{2} + υ_{0} t + y_{0} .$ (17)

Here, $y_{0}$ $y_{0}$ denotes the initial $(t = 0)$ $(t = 0)$ height of the body and $v_{0}$ $v_{0}$ its initial velocity.

Example 3

Projectile motion

Suppose that a ball is thrown straight upward from the ground $(y_{0} = 0)$ $(y_{0} = 0)$ with initial velocity $v_{0} = 96$ $v_{0} = 96$ (ft/s, so we use $g = 32 {ft/s}^{2} in fps units) .$ $g = 32 {ft/s}^{2} in fps units) .$ Then it reaches its maximum height when its velocity (Eq. (16)) is zero,

$υ (t) = - 32 t + 96 = 0,$ $υ (t) = - 32 t + 96 = 0,$

and thus when $t = 3 s .$ $t = 3 s .$ Hence the maximum height that the ball attains is

$y (3) = - \frac{1}{2} \cdot 32 \cdot 3^{2} + 96 \cdot 3 + 0 = 144 (ft)$ $y (3) = - \frac{1}{2} \cdot 32 \cdot 3^{2} + 96 \cdot 3 + 0 = 144 (ft)$

(with the aid of Eq. (17)).
If an arrow is shot straight upward from the ground with initial velocity $v_{0} = 49$ $v_{0} = 49$ (m/s, so we use $g = 9.8 {m/s}^{2} in mks units),$ $g = 9.8 {m/s}^{2} in mks units),$ then it returns to the ground when

$y (t) = - \frac{1}{2} \cdot (9.8) t^{2} + 49 t = (4.9) t (- t + 10) = 0,$ $y (t) = - \frac{1}{2} \cdot (9.8) t^{2} + 49 t = (4.9) t (- t + 10) = 0,$

and thus after 10 s in the air.

A Swimmer’s Problem

Figure 1.2.5 shows a northward-flowing river of width $w = 2 a$ $w = 2 a$ . The lines $x = \pm a$ $x = \pm a$ represent the banks of the river and the y-axis its center. Suppose that the velocity $v_{R}$ $v_{R}$ at which the water flows increases as one approaches the center of the river, and indeed is given in terms of distance x from the center by

υ_{R} = υ_{0} (1 - \frac{x^{2}}{a^{2}}) .

$υ_{R} = υ_{0} (1 - \frac{x^{2}}{a^{2}}) .$ (18)

You can use Eq. (18) to verify that the water does flow the fastest at the center, where $v_{R} = v_{0}$ $v_{R} = v_{0}$ , and that $v_{R} = 0$ $v_{R} = 0$ at each riverbank.

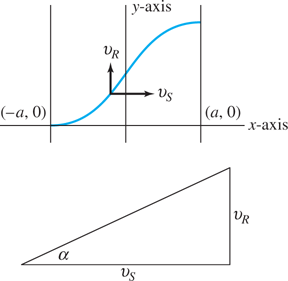
FIGURE 1.2.5.

A swimmer’s problem (Example 4).

Suppose that a swimmer starts at the point $(- a, 0)$ $(- a, 0)$ on the west bank and swims due east (relative to the water) with constant speed $v_{S}$ $v_{S}$ . As indicated in Fig. 1.2.5, his velocity vector (relative to the riverbed) has horizontal component $v_{S}$ $v_{S}$ and vertical component $v_{R}$ $v_{R}$ . Hence the swimmer’s direction angle $α$ $α$ is given by

\tan α = \frac{v_{R}}{v_{S}} .

$\tan α = \frac{v_{R}}{v_{S}} .$

Because $\tan α = d y / d x$ $\tan α = d y / d x$ , substitution using (18) gives the differential equation

\frac{d y}{d x} = \frac{υ_{0}}{υ_{S}} (1 - \frac{x^{2}}{a^{2}})

$\frac{d y}{d x} = \frac{υ_{0}}{υ_{S}} (1 - \frac{x^{2}}{a^{2}})$ (19)

for the swimmer’s trajectory $y = y (x)$ $y = y (x)$ as he crosses the river.

Example 4

River crossing Suppose that the river is 1 mile wide and that its midstream velocity is $v_{0} = 9 mi/h.$ $v_{0} = 9 mi/h.$ If the swimmer’s velocity is $v_{S} = 3 mi/h,$ $v_{S} = 3 mi/h,$ then Eq. (19) takes the form

\frac{d y}{d x} = 3 (1 - 4 x^{2}) .

$\frac{d y}{d x} = 3 (1 - 4 x^{2}) .$

Integration yields

y (x) = \int (3 - 12 x^{2}) d x = 3 x - 4 x^{3} + C

$y (x) = \int (3 - 12 x^{2}) d x = 3 x - 4 x^{3} + C$

for the swimmer’s trajectory. The initial condition $y (- \frac{1}{2}) = 0$ $y (- \frac{1}{2}) = 0$ yields $C = 1$ $C = 1$ , so

y (x) = 3 x - 4 x^{3} + 1 .

$y (x) = 3 x - 4 x^{3} + 1 .$

Then

y (\frac{1}{2}) = 3 (\frac{1}{2}) - 4 {(\frac{1}{2})}^{3} + 1 = 2 .

$y (\frac{1}{2}) = 3 (\frac{1}{2}) - 4 {(\frac{1}{2})}^{3} + 1 = 2 .$

so the swimmer drifts 2 miles downstream while he swims 1 mile across the river.

1.2 Problems

In Problems 1 through 10, find a function $y = f (x)$ $y = f (x)$ satisfying the given differential equation and the prescribed initial condition.

$\frac{d y}{d x} = 2 x + 1$ $\frac{d y}{d x} = 2 x + 1$ ; $y (0) = 3$ $y (0) = 3$
$\frac{d y}{d x} = {(x - 2)}^{2}$ $\frac{d y}{d x} = {(x - 2)}^{2}$ ; $y (2) = 1$ $y (2) = 1$
$\frac{d y}{d x} = \sqrt{x}$ $\frac{d y}{d x} = \sqrt{x}$ ; $y (4) = 0$ $y (4) = 0$
$\frac{d y}{d x} = \frac{1}{x^{2}}$ $\frac{d y}{d x} = \frac{1}{x^{2}}$ ; $y (1) = 5$ $y (1) = 5$
$\frac{d y}{d x} = \frac{1}{\sqrt{x + 2}}$ $\frac{d y}{d x} = \frac{1}{\sqrt{x + 2}}$ ; $y (2) = - 1$ $y (2) = - 1$
$\frac{d y}{d x} = x \sqrt{x^{2} + 9}$ $\frac{d y}{d x} = x \sqrt{x^{2} + 9}$ ; $y (- 4) = 0$ $y (- 4) = 0$
$\frac{d y}{d x} = \frac{10}{x^{2} + 1}$ $\frac{d y}{d x} = \frac{10}{x^{2} + 1}$ ; $y (0) = 0$ $y (0) = 0$
$\frac{d y}{d x} = \cos 2 x$ $\frac{d y}{d x} = \cos 2 x$ ; $y (0) = 1$ $y (0) = 1$
$\frac{d y}{d x} = \frac{1}{\sqrt{1 - x^{2}}}$ $\frac{d y}{d x} = \frac{1}{\sqrt{1 - x^{2}}}$ ; $y (0) = 0$ $y (0) = 0$
$\frac{d y}{d x} = x e^{- x}$ $\frac{d y}{d x} = x e^{- x}$ ; $y (0) = 1$ $y (0) = 1$

In Problems 11 through 18, find the position function x(t) of a moving particle with the given acceleration a(t), initial position $x_{0} = x (0)$ $x_{0} = x (0)$ , and initial velocity $v_{0} = v (0)$ $v_{0} = v (0)$ .

$a (t) = 50$ $a (t) = 50$ , $v_{0} = 10$ $v_{0} = 10$ , $x_{0} = 20$ $x_{0} = 20$
$a (t) = - 20$ $a (t) = - 20$ , $v_{0} = - 15$ $v_{0} = - 15$ , $x_{0} = 5$ $x_{0} = 5$
$a (t) = 3 t$ $a (t) = 3 t$ , $v_{0} = 5$ $v_{0} = 5$ , $x_{0} = 0$ $x_{0} = 0$
$a (t) = 2 t + 1$ $a (t) = 2 t + 1$ , $v_{0} = - 7$ $v_{0} = - 7$ , $x_{0} = 4$ $x_{0} = 4$
$a (t) = 4 {(t + 3)}^{2}$ $a (t) = 4 {(t + 3)}^{2}$ , $v_{0} = - 1, x_{0} = 1$ $v_{0} = - 1, x_{0} = 1$
$a (t) = \frac{1}{\sqrt{t + 4}}$ $a (t) = \frac{1}{\sqrt{t + 4}}$ , $v_{0} = - 1$ $v_{0} = - 1$ , $x_{0} = 1$ $x_{0} = 1$
$a (t) = \frac{1}{{(t + 1)}^{3}}$ $a (t) = \frac{1}{{(t + 1)}^{3}}$ , $v_{0} = 0$ $v_{0} = 0$ , $x_{0} = 0$ $x_{0} = 0$
$a (t) = 50 \sin 5 t$ $a (t) = 50 \sin 5 t$ , $v_{0} = - 10, x_{0} = 8$ $v_{0} = - 10, x_{0} = 8$

Velocity Given Graphically

In Problems 19 through 22, a particle starts at the origin and travels along the x-axis with the velocity function v(t) whose graph is shown in Figs. 1.2.6 through 1.2.9. Sketch the graph of the resulting position function x(t) for $0 ≦ t ≦ 10$ $0 ≦ t ≦ 10$ .

FIGURE 1.2.6.

Graph of the velocity function $υ (t)$ $υ (t)$ of Problem 19.
FIGURE 1.2.7.

Graph of the velocity function $υ (t)$ $υ (t)$ of Problem 20.
FIGURE 1.2.8.

Graph of the velocity function $υ (t)$ $υ (t)$ of Problem 21.
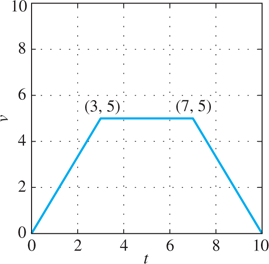
FIGURE 1.2.9.

Graph of the velocity function $υ (t)$ $υ (t)$ of Problem 22.

Problems 23 through 28 explore the motion of projectiles under constant acceleration or deceleration.

What is the maximum height attained by the arrow of part (b) of Example 3?
A ball is dropped from the top of a building 400 ft high. How long does it take to reach the ground? With what speed does the ball strike the ground?
The brakes of a car are applied when it is moving at 100 km/h and provide a constant deceleration of 10 meters per second per second ( ${m/s}^{2}$ ${m/s}^{2}$ ). How far does the car travel before coming to a stop?
A projectile is fired straight upward with an initial velocity of $100 m/s$ $100 m/s$ from the top of a building 20 m high and falls to the ground at the base of the building. Find
1. its maximum height above the ground;
2. when it passes the top of the building;
3. its total time in the air.
A ball is thrown straight downward from the top of a tall building. The initial speed of the ball is 10 m/s. It strikes the ground with a speed of 60 m/s. How tall is the building?
A baseball is thrown straight downward with an initial speed of 40 ft/s from the top of the Washington Monument (555 ft high). How long does it take to reach the ground, and with what speed does the baseball strike the ground?
Variable acceleration A diesel car gradually speeds up so that for the first 10 s its acceleration is given by

$\begin{array}{l} \frac{d υ}{d t} = (0.12) t^{2} + (0.6) t & ({ft/s}^{2}) \end{array} .$ $\begin{array}{l} \frac{d υ}{d t} = (0.12) t^{2} + (0.6) t & ({ft/s}^{2}) \end{array} .$

If the car starts from rest ( $x_{0} = 0, v_{0} = 0$ $x_{0} = 0, v_{0} = 0$ ), find the distance it has traveled at the end of the first 10 s and its velocity at that time.

Problems 30 through 32 explore the relation between the speed of an auto and the distance it skids when the brakes are applied.

A car traveling at 60 mi/h (88 ft/s) skids 176 ft after its brakes are suddenly applied. Under the assumption that the braking system provides constant deceleration, what is that deceleration? For how long does the skid continue?
The skid marks made by an automobile indicated that its brakes were fully applied for a distance of 75 m before it came to a stop. The car in question is known to have a constant deceleration of 20 ${m/s}^{2}$ ${m/s}^{2}$ under these conditions. How fast—in km/h—was the car traveling when the brakes were first applied?
Suppose that a car skids 15 m if it is moving at 50 km/h when the brakes are applied. Assuming that the car has the same constant deceleration, how far will it skid if it is moving at 100 km/h when the brakes are applied?

Problems 33 and 34 explore vertical motion on a planet with gravitational acceleration different than the Earth’s.

On the planet Gzyx, a ball dropped from a height of 20 ft hits the ground in 2 s. If a ball is dropped from the top of a 200-ft-tall building on Gzyx, how long will it take to hit the ground? With what speed will it hit?
A person can throw a ball straight upward from the surface of the earth to a maximum height of 144 ft. How high could this person throw the ball on the planet Gzyx of Problem 33?
Velocity in terms of height A stone is dropped from rest at an initial height h above the surface of the earth. Show that the speed with which it strikes the ground is $v = \sqrt{2 g h}$ $v = \sqrt{2 g h}$ .
Varying gravitational acceleration Suppose a woman has enough “spring” in her legs to jump (on earth) from the ground to a height of 2.25 feet. If she jumps straight upward with the same initial velocity on the moon—where the surface gravitational acceleration is (approximately) $5.3 {ft/s}^{2}$ $5.3 {ft/s}^{2}$ —how high above the surface will she rise?
At noon a car starts from rest at point A and proceeds at constant acceleration along a straight road toward point B. If the car reaches B at 12:50 p.m. with a velocity of 60 mi/h, what is the distance from A to B?
At noon a car starts from rest at point A and proceeds with constant acceleration along a straight road toward point C, 35 miles away. If the constantly accelerated car arrives at C with a velocity of 60 mi/h, at what time does it arrive at C?
River crossing If $a = 0.5 mi$ $a = 0.5 mi$ and $v_{0} = 9 mi/h$ $v_{0} = 9 mi/h$ as in Example 4, what must the swimmer’s speed $v_{S}$ $v_{S}$ be in order that he drifts only 1 mile downstream as he crosses the river?
River crossing Suppose that $a = 0.5$ $a = 0.5$ mi, $v_{0} = 9$ $v_{0} = 9$ mi/h, and $v_{S} = 3$ $v_{S} = 3$ mi/h as in Example 4, but that the velocity of the river is given by the fourth-degree function

$υ_{R} = υ_{0} (1 - \frac{x^{4}}{a^{4}})$ $υ_{R} = υ_{0} (1 - \frac{x^{4}}{a^{4}})$

rather than the quadratic function in Eq. (18). Now find how far downstream the swimmer drifts as he crosses the river.
Interception of bomb A bomb is dropped from a helicopter hovering at an altitude of 800 feet above the ground. From the ground directly beneath the helicopter, a projectile is fired straight upward toward the bomb, exactly 2 seconds after the bomb is released. With what initial velocity should the projectile be fired in order to hit the bomb at an altitude of exactly 400 feet?
Lunar lander A spacecraft is in free fall toward the surface of the moon at a speed of 1000 mph (mi/h). Its retrorockets, when fired, provide a constant deceleration of $20,000 {mi/h}^{2}$ $20,000 {mi/h}^{2}$ . At what height above the lunar surface should the astronauts fire the retrorockets to insure a soft touchdown? (As in Example 2, ignore the moon’s gravitational field.)
Solar wind Arthur Clarke’s The Wind from the Sun (1963) describes Diana, a spacecraft propelled by the solar wind. Its aluminized sail provides it with a constant acceleration of $0.001 g = 0.0098 {m/s}^{2}$ $0.001 g = 0.0098 {m/s}^{2}$ . Suppose this spacecraft starts from rest at time $t = 0$ $t = 0$ and simultaneously fires a projectile (straight ahead in the same direction) that travels at one-tenth of the speed $c = 3 \times 10^{8} m/s$ $c = 3 \times 10^{8} m/s$ of light. How long will it take the spacecraft to catch up with the projectile, and how far will it have traveled by then?
Length of skid A driver involved in an accident claims he was going only 25 mph. When police tested his car, they found that when its brakes were applied at 25 mph, the car skidded only 45 feet before coming to a stop. But the driver’s skid marks at the accident scene measured 210 feet. Assuming the same (constant) deceleration, determine the speed he was actually traveling just prior to the accident.
Kinematic formula Use Eqs. (10) and (11) to show that $v {(t)}^{2} - v_{0}^{2} = 2 a [x (t) - x_{0}]$ $v {(t)}^{2} - v_{0}^{2} = 2 a [x (t) - x_{0}]$ for all t when the acceleration $a = d v / d t$ $a = d v / d t$ is constant. Then use this “kinematic formula”—commonly presented in introductory physics courses—to confirm the result of Example 2.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 1.2 Integrals as General and Particular Solutions

Create new playlist

Sign In

Sign Up

Table of Contents for
1.2 Integrals as General and Particular Solutions