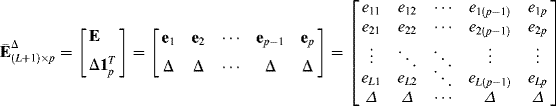7.3 Second-Order Statistics-Based Endmember Extraction
Based on the nature of pure signatures using the concept of convexity geometry as a criterion to find endmembers seems natural and logical, but may not be the only way to accomplish the task of endmember extraction. Instead of appealing for geometric features such as convex hull, convex cone, and simplex described above, a rather different approach that uses the statistical spectral profile of a signature as a base to determine an endmember is of interest. More specifically, a set of spectrally distinct endmembers should constitute the least statistical spectral correlation among all possible data sets with the same number of data samples. In other words, if there is a data sample that is a mixture of other data samples in the same set, the statistical spectral correlation among members in this set should be greater than that of a set with the same number of data samples that are all endmembers. In this section, we explore such statistics-based approaches to endmember extraction. In particular, we are interested in second-order statistics with two criteria, statistical sample spectral correlation and LSE that can be used to design EEAs.
The second-order statistical sample correlation was previously explored by Singh and Harison (1985) who expressed the second-order statistics information in terms of correlation coefficients. Their idea was used by Eklundh and Singh (1993) to develop the so-called standardized principal components analysis (SPCA). Here, we further take advantage of SPCA developed by Eklundh and Singh to derive an approach to endmember extraction, called standardized PCA-based EEA (SPCA-EEA). The key idea behind the proposed SPCA-EEA is to assume that the information represented by correlation coefficients among endmembers is minimal. More specifically, for a given set of p signatures the least amount of second-order statistical information among all possible p signatures is one that is formed by p distinct endmembers. If one of p signatures is a mixed signature by the other (p−1) endmembers, the shared second-order statistical information must be at least equal to or greater than that represented by the p endmembers.
More specifically, let 
be a set of p endmembers and μj and σj be the mean and standard deviation of the jth endmember ej. 
be a normalized endmember matrix. Then we can define an inner product of E as 
. Assume that 
are eigenavlues of K. Then the determinant of K is given by 
and can be used as a criterion to design an SPCA-based EEA as follows.
SPCA-EEA Algorithm
is a set of initial endmembers.
, for 
we normalize 
to zero mean and unit variance by 
, where 
and 
are the mean and standard deviation of 
. Now we form a 
normalized endmember matrix 
. Define the determinant of 
by
, we calculate 
via 
, then let 
and 
. Increase j by one by setting 
and go to step 4. Otherwise, let 
and 
and continue.
, then go to step 4. Otherwise, continue.
with 
. Define 
and 
for 
. If the newly obtained (k + 1)st endmember set 
is identical to the kth endmember set 
, that is, 
, the algorithm is terminated. Otherwise, let 
. Go to step 2.
To demonstrate the utility of SPCA-EEA in endmember extraction Figure 7.11 shows nine endmembers extracted by SPCA-EEA using three different sets of random initial endmembers where only two panel pixels in rows 3 and 5 were extracted to correspond to two endmembers.
Figure 7.11 Nine endmembers extracted by SPCA-EEA using random initial conditions in three different runs.
In order to take into account the mixing coefficients of endmembers constrained by convexity, an FCLS method developed by Heinz and Chang (2001) is included in the proposed SPCA-EEA to ensure that all the SPCA-EEA found endmembers encompass all possible data samples as their mixing signatures.
In order to take care of the sum-to-one constraint into the algorithm, a p-dimensional column vector 
should be included. This is similar to FCLS and N-FINDR. That is, let 
be an 
endmember matrix and 
be a p-dimensional unity vector. We introduce an 
matrix 
by augmenting the matrix E by including a p-dimensional unity vector 1p as follows:
where the parameter Δ is included to control the effect of ASC. It should be noted that (7.21) is the same matrix used in FCLS algorithm in Heinz and Chang (2001), the same endmember matrix E used in N-FINDR and 
used in step 2 of AN-FINDR. In this case, the p-dimensional 
column vector used in step 2 of the PCA-EEA is extended to a (p+1) -dimensional column vector defined by 
.
A note is worthwhile. One may wonder “why cannot we use the commonly used PCA instead of SPCA to design an EEA?”. The answer to this question can be very enlightening. PCA only considers data variances while discarding co-variances that are crucial in endmember extraction. On the other hand, SPCA explores statistical correlation by correlation coefficients that are indeed obtained from both variances and co-variances. However, since an endmember is relatively rare, its presence may be more appropriately characterized by high-order statistics (HOS) rather than second-order statistics such as variance. This fact gives rise to the possibility of using HOS as criteria to develop EEAs, which will be discussed in Chapter 8. One disadvantage of using HOS is that there is no analytical form that can be derived for an HOS-based SM-EEA in a similar way that PCA solves the characteristic polynomial equation to find all eigenvalues simultaneously. Instead, an HOS-based EEA must rely on a numerical algorithm to generate one projection vector to find one endmember at a time. Therefore, an HOS-based EEA is an SQ-EEA and cannot be an SM-EEA.