12.2 Three Perspectives to Derive OSP

Suppose that L is the number of spectral bands and r is an L-dimensional image pixel vector. Assume that there are p targets, and denote their corresponding signatures, which are generally referred to as digital numbers (DN). A linear mixture of r models the spectral signature of r as a linear combination of with appropriate abundance fractions specified by . More precisely, r is an column vector and M is an target spectral signature matrix, denoted by , where m_j is an column vector represented by the spectral signature of the jth target t_j resident in the pixel vector r. Let be a abundance column vector associated with r, where α_j denotes the abundance fraction of the jth target signature m_j present in the pixel vector r.

A classical approach to solving a mixed pixel classification problem is linear unmixing, which assumes that the spectral signature of the pixel vector r is linearly mixed by , the spectral signatures of the p targets, as follows:

(12.1)

where n is noise or can be interpreted as a measurement or model error.

Equation (12.1) represents a standard model for signal detection in noise as s + n, where Mα is considered as a desired signal vector s = Mα needed to be detected and n is a corrupted noise. Since we are interested in detecting one target at a time, we can divide the set of the p targets, into a desired target, say t_p and a class of undesired targets, . In this case, a logical approach is to eliminate the effects caused by the undesired targets that are considered as interferers to t_p before the detection of t_p takes place. With annihilation of the undesired target signatures, the detectability of t_p can therefore be enhanced. In doing so, we refine the signal detection in noise, s + n = Mα + n by first separating m_p from in M and rewrite (12.1) as

(12.2)

where is the desired spectral signature of t_p and is the undesired target spectral signature matrix made up of that are the spectral signatures of the remaining p − 1 undesired targets. Here, without loss of generality we assume that the desired target is a single target t_p and refer (12.2) to the (d,U)-model.

12.2.1 Signal Detection Perspective Derived from (d,U)-Model and OSP-Model

Using the (d,U)-model specified by (12.2) we can design an orthogonal subspace projector to annihilate U from the pixel vector r prior to detection of t_p. One such a desired orthogonal subspace projector is derived in Harsanyi and Chang (1994) and given by

(12.3)

where is the pseudo-inverse of U. The notation indicates that the projector maps the observed pixel vector r into the orthogonal complement of , denoted by .

Applying to (d,U)-model results in a new signal detection in noise model

(12.4)

where the undesired signatures in U have been annihilated and the original noise n has been also suppressed to . The model specified by (12.4) will be referred to as the OSP-model thereafter in this chapter.

At this point, it is noteworthy to comment on distinction among the three models specified by (12.1), (12.2), and (12.4). The model in (12.1) is a general signal detection in noise model that only separates a signal source Mα from noise n. The (d,U)-model is a signal model derived from the general signal detection in noise model by breaking up the considered signal sources into two types of signal sources d and U provided by prior knowledge. It is a two signal-source (d,U)-model that allows us to deal with these two types of signal sources, d,U separately. The OSP-model is a single desired-signal source (d) detection in noise model derived from the (d,U)-model with the U in the (d,U)-model annihilated by . Therefore, OSP-model can be considered as a custom-designed signal detection in noise model from (12.1) where the signal and noise sources in (12.1) have been preprocessed by for signal enhancement as well as noise suppression.

If we operate a linear filter specified by a weighting vector w on the OSP-model, the filter output is given by . One commonly used optimal criterion is maximization of the filter output SNR over the weighting vector w defined by

(12.5)

If we further assume that n is an additive and zero-mean white noise with variance σ², (12.5) can be further reduced to where is an idempotent projector, that is, (Scharf, 1991). The maximum of SNR(w) in (12.5) over w can be obtained by Schwarz's inequality:

(12.6)

where ||x|| is defined by and the equality holds if and only if for some constant κ. That is, a linear optimal filter specified by the weighting vector produces the maximum filter output SNR given by . Such a filter can be realized by a matched filter, defined by

(12.7)

with the matched signal specified by . Applying the matched filter to the OSP-model results in

(12.8)

that yields the maximum SNR, .

Using (12.8) we can design a linear optimal signal detector for (d,U)-model, denoted by δ^OSPD(r) by first implementing an undesired target signature rejecter followed by a matched filter with the matched signal as follows:

(12.9)

that is exactly the one derived in Harsanyi and Chang (1994) with κ = 1.

If δ^OSPD(r) operates the (d,U)-model in (12.2), then the result is identical to (12.8). This suggests that if the (d,U)-model is used, the optimal linear filter in (12.9) requires two filters, and M_d to achieve maximum SNR compared to a single matched filter when OSP-model is used with used as a preprocessing of model (12.1).

12.2.2 Fisher's Linear Discriminant Analysis Perspective from OSP-Model

The OSP-model described by (12.4) can be also interpreted as a two-class classification problem, signal and noise , respectively. Let and be the mean vector and covariance matrix of , and and be the mean vector and covariance matrix of . Let a linear discriminant function y(x) be denoted by a linear form specified by . Fisher's ratio criterion as Rayleigh quotient defined in Duda and Hart (1973) is given by

(12.10)

where and are called between-class and within-class scatter matrices, respectively. So, finding the Fisher linear discriminant function with the weighting vector specified by w^Fisher is equivalent to maximizing (12.10) over the w, which is in turn to solve the following generalized eigenvalue problem (Stark and Woods, 2002, Theorem 5.5.1, pp. 259–260):

(12.11)

If we further assume that the signal is deterministic and the noise is zero-mean, , , , and . Equation (12.10) becomes (12.5) and (12.11) is also further reduced to

(12.12)

Since the rank of the matrix in (12.12) is one, the only nonzero eigenvalue is the maximum eigenvalue λ_max that turns out to be the solution to (12.12). Now, we substitute for w in (12.12), (12.5), and (12.10) and obtain

(12.1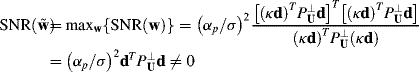3)

(12.14)

and

(12.15)

All of these three equations (i.e., (12.13–12.15)) produce the same result . This implies that is a desired eigenvector that yields the maximum eigenvalue λ_max and can be used to solve both (12.10) and (12.12), in which case becomes w^Fisher, that is, . As a result, Fisher's linear discriminant function for (12.10) or (12.12), denoted by δ^Fisher(r), can be derived as

(12.16)

The above approach to arriving at the Fisher's discriminant function in (12.16) was the same one actually used by Harsanyi and Chang (1994) to derive the OSP classifier, δ^OSP(r) given by

(12.17)

Interestingly, the solution obtained from the signal detection perspective is different from OSP solution and the solution obtained from Fisher's linear discriminant function in that the undesired target signature projector appearing in w^∗ is absent in w^OSP and w^Fisher. However, if we substitute for w in (12.12), (12.13)–(12.15), we still obtain the same result, . This implies that both and produce the same maximum eigenvalue, . Therefore, OSP-based signal detector, δ^OSPD(r) specified by (12.9) is actually δ^Fisher(r) and Harsanyi–Chang's OSP, δ^OSP(r) specified by (12.16) and (12.17) subject to a constant κ.

It should be also noted that if the between-class scatter matrix and within-class scatter matrix in Fisher's Rayleigh quotient or ratio given in (12.10) are replaced with the data covariance matrix Σ and noise covariance matrix as follows:

(12.18)

then using the same assumptions made for (12.12) (i.e., , , and ) maximizing (12.18) over w is identical to solving (12.12) for w. In this case, Fisher's Rayleigh quotient or ratio in (12.10) can be interpreted as SNR.

12.2.3 Parameter Estimation Perspective from OSP-Model

In signal detection the primary task is to detect the desired target t_p in noise using (12.1). As shown in the above derivations, using OSP-model specified by (12.4) can improve and increase signal detectability of using (12.1). In pattern classification, the desired target signal t_p is discriminated from noise using a between-class scatter matrix/within-class scatter matrix criterion specified by (12.10). Both of these approaches do not intend to estimate its desired signature abundance fraction α_p. In this subsection, we look into a least squares (LS) approach to estimating the abundance fraction α_p of the desired target signature d. Using OSP-model and least squares error (LSE) as a criterion for optimality, we can show that the LS estimate of α_p, minimizing

(12.19)

is also the LS solution to LSMA using (12.1) as a model to perform spectral unmixing.

Differentiating (12.19) with respect to α_p and setting it to zero results in

(12.20)

that yields the solution to (12.19), denoted by and given by

(12.21)

Comparing to δ^OSP(r), there is a scaling constant appearing in , but absent in δ^OSP(r). In other words, (12.17) and (12.21) are related by

(12.22)

where the scaling constant is the consequence of LSE resulting from the estimation problem using the OSP-model in (12.19). This constant is included to account for estimation accuracy, not treated as a normalization constant as commonly assumed.

It should be noted that the approach presented above to re-derive δ^OSP(r) is different from that developed in (Tu et al., 1997; Chang, 1998, 2003a; Chang et al., 1998), all of which use the oblique subspace projection (Scharf, 1991).

12.2.4 Relationship Between and Least-Squares Linear Spectral Mixture Analysis

In order to see how is related to the commonly used LS-LSMA, we minimize the LSE resulting from (12.1) as follows:

(12.23)

The LS solution to (12.23), denoted by is given by Scharf (1991)

(12.24)

The major difference between and is that the former is a scalar parameter estimate of α_p, whereas the latter is a vector parameter estimate of the abundance vector α. It has been shown in Settle (1996) that can be decomposed as with

(12.25)

where is the LS estimated abundance vector of and . Combining (12.22) and (12.25) results in

(12.26)

where is the pth component of in (12.25) and also the LS estimate of α_p in (12.22). The same argument can be carried out for all other abundance fractions, . If we let and , then

(12.27)

where for .

Now, we further introduce the jth component projection function 1_j defined by

(12.28)

then we can rewrite (12.27) as

(12.29)

where (12.26) is its particular case.

In light of (12.29), (12.25)–(12.28), if operates on every individual signature with m being the jth signature in M, it becomes the commonly used linear spectral unmixing solution, . Compared to that solves for all p abundance fractions as a vector, the advantage of using over is conceptually easy to understand and mathematically simple to implement. In other words, if we are interested in detection or estimation of a target signature of particular interest, all we have to do is (1) to designate this target signature as d, (2) to annihilate all signatures other than d in U by , and (3) to extract d using a matched filter with the matched signature specified by d. This is equivalent to using OSP-model to estimate the abundance fraction of d after the undesired target signatures have been annihilated by rather than using to directly estimate the entire abundance fractions via (12.24). More specifically, if the LS estimation is performed for (12.24) using OSP-model, then (12.24) is reduced to

(12.30)

where is the LS estimate of α_j based on the (d,U)-model in (12.2) with d replaced by m_j and U set by . As a consequence, (12.30) is exactly identical to (12.29). Both (12.29) and (12.30) suggest two different ways to estimate the abundance fraction α_j for . In other words, (12.30) first projects the data to the space that is orthogonal to the space linearly spanned by the undesired target signatures in U using , then LS estimates the abundance fraction of the desired target signature, d. This is actually the approach taken by OSP in (12.17). In contrast, (12.29) is the commonly used LS-LSMA that performs a vector parameter estimation, then uses a projection function defined by (12.28) to yield the abundance fraction of the desired target signature, d. The relationship between these two equations is delivered by (12.28) and (12.30), which were overlooked in the past. This is very important because many subspace-based vector parameter estimation methods can be interpreted by OSP via (12.25)–(12.30). A diagram to illustrate relationships among OSP, the least squares OSP and the LS-LSMA is depicted in Figure 12.1 where the abundance fraction α_j is estimated.

Figure 12.1 Diagram of relationships among OSP, least-squares OSP and least-squares LSMA.

As a concluding remark, it is worth noting that the idea of using OSP-model to re-derive OSP provides new insights into OSP, particularly, the approaches to linear discriminant analysis and parameter estimation, and the relationship between OSP and the LS-LSMA via OSP-model.