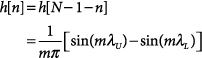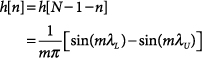Note 35. Designing FIR Filters: Basic Window Method
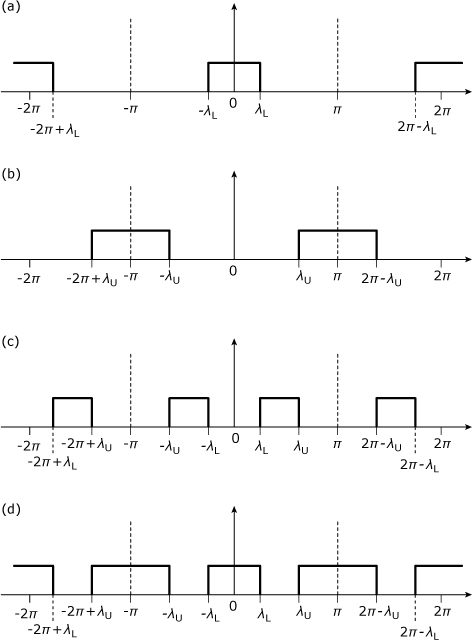
The window method of FIR design is based on the fact that the frequency response of a digital filter is periodic, and therefore can be represented as a Fourier series. A template for the desired frequency response is selected and expanded as a Fourier series. This expansion is then truncated to finite-number terms by multiplying the sequence of Fourier series coefficients with a sequence of samples obtained from a time-limited window function. The resulting finite sequence of terms is then used as the coefficients for an FIR filter. This filter has a frequency response that approximates the original desired response. When a rectangular window is used to truncate the coefficient sequence, the window method is called the Fourier series method.
Recipe 35.1. Fourier Series Method for FIR Filter Design
The following steps detail the basic strategy for using the Fourier series method. This strategy is specialized to specific band configurations in Recipes 35.2 through 35.5.
- Specify a desired response, Hd (λ), as a function of normalized continuous radian frequency λ for –π ≤ λ ≤ π.
- Specify the desired number of filter taps, N.
- Compute the filter coefficients h[n] for n = 0, 1, 2, . . ., N –1 using
where m = n – (N–1)/2. When Hd (λ) is even symmetric, computation of the coefficients simplifies to
- Using the DTFT, compute the frequency response of the filter defined by h[n]. If the performance is not adequate, modify N and/or Hd (λ), and repeat step 3.
Recipe 35.2. Approximating the Ideal Lowpass Filter
Perform the following steps to approximate the ideal lowpass filter response depicted in Figure 35.1(a).
- Specify the desired cutoff frequency, λU.
- Determine the desired number of filter taps, N.
- For n = 0, 1, 2, . . .,
, compute h[n] and h[N – 1– n] as
where m = n – (N–1)/2. The notation
x
indicates the ceiling function, which has a value equal to the largest integer, less than or equal to x. - If N is odd, compute h[(N – 1)/2] as
Figure 35.1. Frequency response for ideal digital filters: (a) lowpass, (b) highpass, (c) bandpass, and (d) bandstop
Recipe 35.3. Approximating the Ideal Highpass Filter
Perform the following steps to approximate the ideal lowpass filter response depicted in Figure 35.1(b).
- Specify the desired cutoff frequency, λL.
- Determine the desired number of filter taps, N.
- For n = 0, 1, 2, . . .,
, compute h[n] and h[N – 1– n] as
where m = n – (N–1)/2.
- If N is odd, compute h[(N – 1)/2] as
Recipe 35.4. Approximating the Ideal Bandpass Filter
Perform the following steps to approximate the ideal bandpass filter response depicted in Figure 35.1(c).
- Specify the desired lower cutoff frequency, λL, and the upper cutoff frequency, λU.
- Determine the desired number of filter taps, N.
- For n = 0, 1, 2, . . .,
, compute h[n] and h[N – 1– n] as
where m = n – (N–1)/2.
- If N is odd, compute h[(N – 1)/2] as
Recipe 35.5. Approximating the Ideal Bandstop Filter
Perform the following steps to approximate the ideal bandpass filter response depicted in Figure 35.1(d).
- Specify the desired lower cutoff frequency, λL, and the upper cutoff frequency, λU.
- Determine the desired number of filter taps, N.
- For n = 0, 1, 2, . . .,
, compute h[n] and h[N – 1– n] as
where m = n – (N–1)/2.
- If N is odd, compute h[(N – 1)/2] as
References
1. D. Slepian and H. Pollak, “Prolate-Spheroidal Wave Functions, Fourier Analysis and Uncertainty-I,” Bell Syst. Tech. J., vol. 40, January 1961, pp. 43–64.
2. J. F. Kaiser, “Digital Filters,” Chapter 7 in System Analysis by Digital Computer, F. F. Kuo and J. F. Kaiser eds., John Wiley & Sons, 1966.
3. J. F. Kaiser, “Nonrecursive Digital Filter Design Using the I0sinh Window Function,” Proc. 1974 IEEE Int. Symp. on Circuits and Syst., April 22–25, 1974, pp. 20–23.
4. A. Antoniou, Digital Filters: Analysis and Design, McGraw-Hill, 1979.
5. f. j. harris, “On the Use of Windows for Harmonic Analysis with the Discrete Fourier Transform,” Proc. IEEE, vol. 66, no. 1, January 1978, pp. 51–83.