8.3. Assessing Dose Linearity

As discussed in the introduction, when an oral tablet is taken it will be absorbed, distributed, metabolized and eliminated. Imagine that the body is made up of many different compartments. The drug amount that enters circulation is then both simultaneously distributed into and eliminated from these compartments. Typically, a drug is eliminated from the body through urine or feces. In order to facilitate this process, the liver often metabolizes the compound to a chemical form that is more readily eliminated. If all of the eliminations from one compartment to another are proportional to the concentration of the compound in the compartment, the drug has dose linearity. Dose linearity implies that the elimination rate from the body is proportional as well.

The following two conditions are therefore implied. First, the elimination rate is proportional to drug concentration with k denoting the proportion. This constant is often replaced with clearance. As can be seen, dose linearity implies that clearance is a constant. Second, with repeated dosing there exists a point in time in which there is an equilibrium between the amount of drug that enters the body and the amount that leaves. Once this equilibrium has been reached, the drug is said to have achieved steady state.

As can be seen, it would be impossible to really tell if a drug were truly dose linear; however, a drug that has dose linearity (or that at least approximates dose linearity) should have certain properties. One of these is a proportional increase in concentration in the blood or plasma as measured with AUC and C_max, with increasing dose. This situation is often referred to as dose proportionality. A second property is that the clearance ought to be stationary with time. Both of these properties can be studied in human pharmacokinetic studies.

8.3.1. Assessing Dose Proportionality

Dose proportionality is a proportional increase in concentration as measured with AUC and C_max, with increasing dose. Using AUC, this implies that

AUC = αd,

where d represents the dose. There are many different models to examine dose proportionality. A discussion to the relative merits and demerits of these models can be found is Smith (2004). This section will focus on the following model

ln AUC = α + β ln d.

This model is referred to as the power model on an ln-transformed AUC. The same model is used for C_max as discussed in the previous section. Notice that when we exponentiate both sides of this equation we have

AUC = exp(α)d^β.

Thus, when β = 1, the drug is dose proportional.

In assessing dose proportionality, we may first consider a hypothesis test of the following

H₀ : β = 1.

We may consider declaring dose proportionality if we fail to reject this hypothesis. Smith et al. (2000) argue that it is much more natural to think of dose proportionality as an equivalence problem, implying that the structure for testing dose proportionality should be

Unlike bioequivalence, the equivalence region currently has no set regulatory standard. Smith et al. (2000) considers the following:

Smith et al. (2000) show that this structure is equivalent to the structure of H₀₁ and H₀₂ with t = ln θ/ln r. Notice that t → ∞ when r → 1 and t → 0 when r ∞. Thus, there exists a set of r's such that both H₀₁ and H₀₂ will be rejected.

The largest of these r's becomes the largest ratio of doses for which dose proportionality can be declared. Smith et al. (2000) show that if H₀₁ and H₀₂ are tested at the α level and that if L and H define the lower and upper limit of a (1 −2α)100% confidence interval, this largest ratio ρ₁ is

Furthermore, Smith et al. (2000) describe three possible conclusions that can be drawn about dose proportionality:

"Definitely not dose proportional" is concluded if either the null hypothesis H₀₁ or the null hypothesis H₀₂ cannot be rejected. Smith et al. (2000) show that sometimes there exists a smallest ratio, ρ₂, in which dose proportionality definitely does not exist and is given by

It should be pointed out that this equation cannot be solved unless L > 1 or U < 1.

Data for examination of dose proportionality most often comes from first human, dose escalation type trials in which randomization-to-period is not done. Occasionally, a stand-alone study is performed to ensure that period effects do not confound inference.

EXAMPLE: First human-dose study

Consider the simulated data from a hypothetical first human dose trial (FHDAUC data set can be found on the book's companion Web site). Here 16 subjects received ascending doses of drug, and AUC(0-∞) [ng/mL/h] was measured after each administration.

Program 8.3 shows how to perform the dose proportionality analysis of the AUC data using a random-intercept model in PROC MIXED.

Example 8-3. Analysis of AUC data from the first human-dose study

data fhdauc;
    set fhdauc;
    lndose=log(dose);
    lnauc=log(auc);
    study=1;
proc mixed data=fhdauc method=reml;
    class subject;
    model lnauc=lndose/s ddfm=kenwardroger cl alpha=0.1;
    random subject;
    ods output solutionf=one;
data one;
    set one;
    if effect='lndose' then delete;
    rho1=(4/3)**(1/max(1-lower,upper-1));
    if lower < 1 and upper > 1 then rho2=.;
    else rho2=(4/3)**(1/max(lower−1,1−upper));
proc print data=one noobs;
    var rho1 rho2;
    run;

Example. Output from Program 8.3

Covariance Parameter Estimates

 Cov Parm     Estimate

 subject       0.04175
 Residual      0.01861

         Solution for Fixed Effects

                       Standard
Effect      Estimate      Error     DF   t Value   Pr > |t|

Intercept    −0.2583    0.07518   36.9     −3.44     0.0015
lndose        1.0395    0.01235   30.7     84.20     <.0001

Effect      Alpha     Lower      Upper

Intercept    0.1     −0.3851    −0.1314
lndose       0.1      1.0186     1.0605

        Type 3 Tests of Fixed Effects

              Num     Den
Effect         DF      DF    F Value    Pr > F

lndose          1    30.7    7088.96    <.0001


     rho1        rho2

   116.630    5344869.90

Output 8.3 shows that β significantly differs from unity (p < 0.0001) with 90% confidence bounds of (1.0186, 1.0605). Between-subject variation in ln-AUC was 0.0418, and within-subject variation was observed to be 0.0186.

Output 8.3 also extracts information from PROC MIXED in order to calculate ρ₁ and ρ₂. Notice that θ = 4/3 in Program 8.3. The choice for θ is user-defined. In this case the resulting equivalence region is (0.75, 1.33), as compared to the equivalence region for bioequivalence of (0.80, 1. 25). Dose proportionality is concluded as the 90% confidence interval for β falls within these limits.

In this first human-dose study, one derives ρ₁ = 117 and ρ₂ = 5,340,000. One would interpret this to mean that dose proportionality has been demonstrated up to a 117-fold range of doses. Said another way, if we knew the concentration (c) for some dose a, then a good prediction of the concentration for a dose 117a would be 117c. The value of ρ₂ in this case is so large that it has little practical meaning. All and all, since it is unlikely in clinical practice to have available a 117-fold range of doses, this molecule demonstrates a significant degree of dose proportionality.

Note that, in this example, ρ₁ = 117 and the dose range studied is 200-fold. It is quite possible for ρ₁ to be greater than the dose range studied. This brings up the question of how we should interpret ρ₁ if this is the case. Assume that in this example ρ₁ turned out to be 500. There would obviously be danger in saying that a good prediction of the concentration for a dose 500a would be 500c, since we are obviously extrapolating beyond available data. With this said, however, it is still useful to think of ρ₁ as a measure of dose proportionality. That is, a value of 500 indicates a greater degree of dose proportionality than a value of 300 would have.

There are certainly other covariance structures that could be chosen in Program 8.3. For instance, a random intercept and slope model can be generated with the following RANDOM statement:

random subject subject*lndose;

8.3.2. Assessing Time Stationarity of Clearance

In the beginning of this section, clearance was defined as the rate of elimination divided by the concentration. When an oral dose is administered, only a fraction of the total dose is absorbed by the body. It can be shown that for a single dose of a drug that

where F is the fraction adsorbed, d is the dose and AUC(0 − ∞) is what has been called AUC so far in this chapter. On the other hand, when a drug is at steady state, it can be shown that

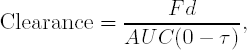
where τ is the dosing interval (24 hours if dosed once a day), d is the amount of drug delivered at each dosing interval, and AUC(0 − τ) is the area under the concentration when the drug is at steady state. The implication of these two formulas is that if AUC(0 − ∞) = AUC(0 − τ) for one dose, then clearance does not change with repeated dosing. If this is true for all doses, then clearance is said to be stationary. Dose linearity implies that clearance is a constant, which implies stationarity.

If the half-life of a drug is short enough, it may be possible to calculate AUC(0 − ∞) for each individual in the first day of dosing of a multiple dose study and find AUC(0-τ) at the last day. Subjects must be at steady state and measures should be taken to ensure this.

The shorter the half-life, the quicker steady state can be achieved. Thus, since we need a short half-life to be able to do this, the drug would most likely be at steady state. Having a short enough half-life to be able to use day 1 data, however, is pretty unlikely.

Another possibility is doing the first human dose study in the same subjects as the multiple dose study. Usually, when this is done, these studies are combined into one protocol. Again, however, the opportunity to do this does not present itself very often. The reason these options are appealing is it allows us to use a subject as its own control. The most common case, however, is that the first human dose study and multiple dose study are done in separate groups of subjects. We can, however, still combine this information to examine stationarity of clearance.

EXAMPLE: Multiple-dose study

Consider the MDAUC data set that can be found on the book's companion Web site. The data set contains simulated data from a hypothetical multiple-dose study. This study tested the compound examined in the first human-dose trial described above. It is assumed that the multiple-dose study was performed in a different set of subjects from the first study. Here, 16 subjects were dosed with 20 to 200 mg of drug repeatedly for several days, and AUC(0-τ) [ng/mL/h] was measured over the dosing interval on the final day.

Program 8.4 examines stationarity of clearance in the multiple-dose study using PROC MIXED. Stationarity of clearance would be concluded if the estimated geometric means from the 20 mg first human dose trial and estimated geometric means from the 20 mg multiple dose trial are equivalent and the estimated geometric means from the 200 mg first human dose trial and estimated geometric means from the 200 mg multiple dose trial are equivalent.

The PROC MIXED code in Program 8.4 fits a separate power model for both studies. The ESTIMATE statements are then used to derive estimates for the single dose mean AUC at 20 mg, the multiple dose mean AUC at 20 mg, their ratio, the single dose mean at 200 mg, the multiple dose mean at 200 mg, and their ratio, respectively. These estimates are saved in the OUT data set and then exponentially transformed to the original scale in order to compute 90% confidence intervals for each scenario. Program 8.4 suppresses the standard PROC MIXED output using ODS LISTING statements. Note that the log-doses of 20 and 200 mg are denoted as 2.995732 and 5.298317, respectively.

Example 8-4. Analysis of AUC data from the multiple-dose study

data mdauc;
    set mdauc;
    lnauc=log(auc);
    lndose=log(dose);
    study=2;
* Merge the data from the first human-dose and multiple-dose studies;
data cl;
    set fhdauc mdauc;
ods listing close;
proc mixed data=cl method=reml;
    class subject study;
    model lnauc=lndose study lndose*study/ddfm=kenwardroger cl alpha=0.1;
    random subject*study;
    estimate "Single dose AUC 20 mg' intercept 1 lndose 2.995732
        study 1 lndose*study 2.995732;
    estimate "Multiple dose AUC 20 mg' intercept 1 lndose 2.995732
        study 1 lndose*study 0 2.995732;
    estimate "Ratio single dose:multiple dose 20 mg' study 1 −1
        lndose*study 2.995732 −2.995732/cl alpha=0.1;

estimate 'Single dose AUC 200 mg' intercept 1 lndose 5.298317
        study 1 lndose*study 5.298317;
    estimate 'Multiple dose AUC 200 mg' intercept 1 lndose 5.298317
        study 0 1 lndose*study 0 5.298317;
    estimate 'Ratio single dose:multiple dose 200 mg' study 1 −1
        lndose*study 5.298317 −5.298317/cl alpha=0.1;
    ods output estimates=out;
data out;
    set out;
    gmean=exp(estimate);
    lbound=exp(lower);
    ubound=exp(upper);
    drop estimate stderr df tvalue alpha lower upper;
proc print data=out noobs;
    ods listing;
    run;

Example. Output from Program 8.4

Label                                  Probt  gmean   lbound  ubound

 Single dose AUC 20 mg                   <.0001 17.385  15.617  19.354
 Multiple dose AUC 20 mg                 <.0001 16.738  13.697  20.455
 Ratio single dose:multiple dose 20 mg   0.7371 1.039   0.860   1.255
 Single dose AUC 200 mg                  <.0001 190.365 170.987 211.939
 Multiple dose AUC 200 mg                <.0001 214.759 177.887 259.273
 Ratio single dose:multiple dose 200 mg  0.2667 0.886   0.740   1.062

Output 8.4 lists the estimated geometric means and associated 90% confidence limits. The 90% confidence interval of the ratio of geometric means for 20 mg is (0.860, 1.255) and the 90% confidence interval of the ratio of geometric mean for 200 mg is (0.740, 1.062). Although neither confidence interval meets the strict bioequivalence (0.8, 1.25) criteria, at this point of drug development, given the limited amount of data, stationarity of clearance would be assumed, until and unless compelling future data indicated otherwise.

Since dose proportionality can be concluded and dose stationarity seems highly tenable, this molecule seems to exhibit dose linearity.