10.6 Evaluation of Clustering
By now you have learned what clustering is and know several popular clustering methods. You may ask, “When I try out a clustering method on a data set, how can I evaluate whether the clustering results are good?” In general, cluster evaluation assesses the feasibility of clustering analysis on a data set and the quality of the results generated by a clustering method. The major tasks of clustering evaluation include the following:
■ Assessing clustering tendency. In this task, for a given data set, we assess whether a nonrandom structure exists in the data. Blindly applying a clustering method on a data set will return clusters; however, the clusters mined may be misleading. Clustering analysis on a data set is meaningful only when there is a nonrandom structure in the data.
■ Determining the number of clusters in a data set. A few algorithms, such as k-means, require the number of clusters in a data set as the parameter. Moreover, the number of clusters can be regarded as an interesting and important summary statistic of a data set. Therefore, it is desirable to estimate this number even before a clustering algorithm is used to derive detailed clusters.
■ Measuring clustering quality. After applying a clustering method on a data set, we want to assess how good the resulting clusters are. A number of measures can be used. Some methods measure how well the clusters fit the data set, while others measure how well the clusters match the ground truth, if such truth is available. There are also measures that score clusterings and thus can compare two sets of clustering results on the same data set.
In the rest of this section, we discuss each of these three topics.
10.6.1 Assessing Clustering Tendency
Clustering tendency assessment determines whether a given data set has a non-random structure, which may lead to meaningful clusters. Consider a data set that does not have any non-random structure, such as a set of uniformly distributed points in a data space. Even though a clustering algorithm may return clusters for the data, those clusters are random and are not meaningful.
“How can we assess the clustering tendency of a data set?” Intuitively, we can try to measure the probability that the data set is generated by a uniform data distribution. This can be achieved using statistical tests for spatial randomness. To illustrate this idea, let’s look at a simple yet effective statistic called the Hopkins Statistic.
The Hopkins Statistic is a spatial statistic that tests the spatial randomness of a variable as distributed in a space. Given a data set, D, which is regarded as a sample of a random variable, o, we want to determine how far away o is from being uniformly distributed in the data space. We calculate the Hopkins Statistic as follows:
1. Sample n points, p1, …, pn, uniformly from D. That is, each point in D has the same probability of being included in this sample. For each point, pi, we find the nearest neighbor of pi (1 ≤ i ≤ n) in D, and let xi be the distance between pi and its nearest neighbor in D. That is,
(10.25)
2. Sample n points, q1, …, qn, uniformly from D. For each qi (1 ≤ i ≤ n), we find the nearest neighbor of qi in D − {qi}, and let yi be the distance between qi and its nearest neighbor in D − {qi}. That is,
(10.26)
3. Calculate the Hopkins Statistic, H, as
(10.27)
“What does the Hopkins Statistic tell us about how likely data set D follows a uniform distribution in the data space?” If D were uniformly distributed, then 
and 
would be close to each other, and thus H would be about 0.5. However, if D were highly skewed, then 
would be substantially smaller than 
in expectation, and thus H would be close to 0.
Our null hypothesis is the homogeneous hypothesis —that D is uniformly distributed and thus contains no meaningful clusters. The nonhomogeneous hypothesis (i.e., that D is not uniformly distributed and thus contains clusters) is the alternative hypothesis. We can conduct the Hopkins Statistic test iteratively, using 0.5 as the threshold to reject the alternative hypothesis. That is, if H > 0.5, then it is unlikely that D has statistically significant clusters.
10.6.2 Determining the Number of Clusters
Determining the “right” number of clusters in a data set is important, not only because some clustering algorithms like k-means require such a parameter, but also because the appropriate number of clusters controls the proper granularity of cluster analysis. It can be regarded as finding a good balance between compressibility and accuracy in cluster analysis. Consider two extreme cases. What if you were to treat the entire data set as a cluster? This would maximize the compression of the data, but such a cluster analysis has no value. On the other hand, treating each object in a data set as a cluster gives the finest clustering resolution (i.e., most accurate due to the zero distance between an object and the corresponding cluster center). In some methods like k-means, this even achieves the best cost. However, having one object per cluster does not enable any data summarization.
Determining the number of clusters is far from easy, often because the “right” number is ambiguous. Figuring out what the right number of clusters should be often depends on the distribution’s shape and scale in the data set, as well as the clustering resolution required by the user. There are many possible ways to estimate the number of clusters. Here, we briefly introduce a few simple yet popular and effective methods.
A simple method is to set the number of clusters to about 
for a data set of n points. In expectation, each cluster has 
points.
The elbow method is based on the observation that increasing the number of clusters can help to reduce the sum of within-cluster variance of each cluster. This is because having more clusters allows one to capture finer groups of data objects that are more similar to each other. However, the marginal effect of reducing the sum of within-cluster variances may drop if too many clusters are formed, because splitting a cohesive cluster into two gives only a small reduction. Consequently, a heuristic for selecting the right number of clusters is to use the turning point in the curve of the sum of within-cluster variances with respect to the number of clusters.
Technically, given a number, k > 0, we can form k clusters on the data set in question using a clustering algorithm like k-means, and calculate the sum of within-cluster variances, var(k). We can then plot the curve of var with respect to k. The first (or most significant) turning point of the curve suggests the “right” number.
More advanced methods can determine the number of clusters using information criteria or information theoretic approaches. Please refer to the bibliographic notes for further information (Section 10.9).
The “right” number of clusters in a data set can also be determined by cross-validation, a technique often used in classification (Chapter 8). First, divide the given data set, D, into m parts. Next, use m − 1 parts to build a clustering model, and use the remaining part to test the quality of the clustering. For example, for each point in the test set, we can find the closest centroid. Consequently, we can use the sum of the squared distances between all points in the test set and the closest centroids to measure how well the clustering model fits the test set. For any integer k > 0, we repeat this process m times to derive clusterings of k clusters by using each part in turn as the test set. The average of the quality measure is taken as the overall quality measure. We can then compare the overall quality measure with respect to different values of k, and find the number of clusters that best fits the data.
10.6.3 Measuring Clustering Quality
Suppose you have assessed the clustering tendency of a given data set. You may have also tried to predetermine the number of clusters in the set. You can now apply one or multiple clustering methods to obtain clusterings of the data set. “How good is the clustering generated by a method, and how can we compare the clusterings generated by different methods?”
We have a few methods to choose from for measuring the quality of a clustering. In general, these methods can be categorized into two groups according to whether ground truth is available. Here, ground truth is the ideal clustering that is often built using human experts.
If ground truth is available, it can be used by extrinsic methods, which compare the clustering against the group truth and measure. If the ground truth is unavailable, we can use intrinsic methods, which evaluate the goodness of a clustering by considering how well the clusters are separated. Ground truth can be considered as supervision in the form of “cluster labels.” Hence, extrinsic methods are also known as supervised methods, while intrinsic methods are unsupervised methods.
Let’s have a look at simple methods from each category.
Extrinsic Methods
When the ground truth is available, we can compare it with a clustering to assess the clustering. Thus, the core task in extrinsic methods is to assign a score, 
, to a clustering, 
, given the ground truth, 
. Whether an extrinsic method is effective largely depends on the measure, Q, it uses.
In general, a measure Q on clustering quality is effective if it satisfies the following four essential criteria:
■ Cluster homogeneity. This requires that the more pure the clusters in a clustering are, the better the clustering. Suppose that ground truth says that the objects in a data set, D, can belong to categories L1, …, Ln. Consider clustering, 
, wherein a cluster 
contains objects from two categories Li, Lj (1 ≤ i < j ≤ n). Also consider clustering 
, which is identical to 
except that C2 is split into two clusters containing the objects in Li and Lj, respectively. A clustering quality measure, Q, respecting cluster homogeneity should give a higher score to 
than 
, that is, 
.
■ Cluster completeness. This is the counterpart of cluster homogeneity. Cluster completeness requires that for a clustering, if any two objects belong to the same category according to ground truth, then they should be assigned to the same cluster. Cluster completeness requires that a clustering should assign objects belonging to the same category (according to ground truth) to the same cluster. Consider clustering 
, which contains clusters C1 and C2, of which the members belong to the same category according to ground truth. Let clustering 
be identical to 
except that C1 and C2 are merged into one cluster in 
. Then, a clustering quality measure, Q, respecting cluster completeness should give a higher score to 
, that is, 
.
■ Rag bag. In many practical scenarios, there is often a “rag bag” category containing objects that cannot be merged with other objects. Such a category is often called “miscellaneous,” “other,” and so on. The rag bag criterion states that putting a heterogeneous object into a pure cluster should be penalized more than putting it into a rag bag. Consider a clustering 
and a cluster 
such that all objects in C except for one, denoted by o, belong to the same category according to ground truth. Consider a clustering 
identical to 
except that o is assigned to a cluster C′ ≠ C in 
such that C′ contains objects from various categories according to ground truth, and thus is noisy. In other words, C′ in 
is a rag bag. Then, a clustering quality measure Q respecting the rag bag criterion should give a higher score to 
, that is, 
.
■ Small cluster preservation. If a small category is split into small pieces in a clustering, those small pieces may likely become noise and thus the small category cannot be discovered from the clustering. The small cluster preservation criterion states that splitting a small category into pieces is more harmful than splitting a large category into pieces. Consider an extreme case. Let D be a data set of n + 2 objects such that, according to ground truth, n objects, denoted by o1, …, on, belong to one category and the other two objects, denoted by on+1, on+2, belong to another category. Suppose clustering 
has three clusters, C1 = {o1, …, on}, C2 = {on+1}, and C3 = {on+2}. Let clustering 
have three clusters, too, namely C1 = {o1, …, on-1}, C2 = {on}, and C3 = {on+1, on+2}. In other words, C1 splits the small category and C2 splits the big category. A clustering quality measure Q preserving small clusters should give a higher score to 
, that is, 
.
Many clustering quality measures satisfy some of these four criteria. Here, we introduce the BCubed precision and recall metrics, which satisfy all four criteria.
BCubed evaluates the precision and recall for every object in a clustering on a given data set according to ground truth. The precision of an object indicates how many other objects in the same cluster belong to the same category as the object. The recall of an object reflects how many objects of the same category are assigned to the same cluster.
Formally, let D = {o1, …, on} be a set of objects, and 
be a clustering on D. Let L (oi) (1 ≤ i ≤ n) be the category of oi given by ground truth, and C(oi) be the cluster_ID of oi in 
. Then, for two objects, oi and oj, (1 ≤ i, j, ≤ n, i ≠ j), the correctness of the relation between oi and oj in clustering 
is given by
(10.28)
BCubed precision is defined as
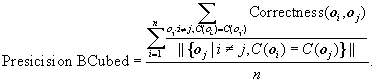(10.29)
BCubed recall is defined as
(10.30)
Intrinsic Methods
When the ground truth of a data set is not available, we have to use an intrinsic method to assess the clustering quality. In general, intrinsic methods evaluate a clustering by examining how well the clusters are separated and how compact the clusters are. Many intrinsic methods have the advantage of a similarity metric between objects in the data set.
The silhouette coefficient is such a measure. For a data set, D, of n objects, suppose D is partitioned into k clusters, C1, …, Ck. For each object o ∈ D, we calculate a (o) as the average distance between o and all other objects in the cluster to which o belongs. Similarly, b(o) is the minimum average distance from o to all clusters to which o does not belong. Formally, suppose o ∈Ci (1 ≤ i ≤ k); then
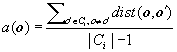(10.31)
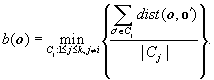(10.32)
The silhouette coefficient of o is then defined as
(10.33)
The value of the silhouette coefficient is between −1 and 1. The value of a(o) reflects the compactness of the cluster to which o belongs. The smaller the value, the more compact the cluster. The value of b(o) captures the degree to which o is separated from other clusters. The larger b(o) is, the more separated o is from other clusters. Therefore, when the silhouette coefficient value of o approaches 1, the cluster containing o is compact and o is far away from other clusters, which is the preferable case. However, when the silhouette coefficient value is negative (i.e., b(o) < a(o)), this means that, in expectation, o is closer to the objects in another cluster than to the objects in the same cluster as o. In many cases, this is a bad situation and should be avoided.
To measure a cluster’s fitness within a clustering, we can compute the average silhouette coefficient value of all objects in the cluster. To measure the quality of a clustering, we can use the average silhouette coefficient value of all objects in the data set. The silhouette coefficient and other intrinsic measures can also be used in the elbow method to heuristically derive the number of clusters in a data set by replacing the sum of within-cluster variances.