7.4 Mining High-Dimensional Data and Colossal Patterns
The frequent pattern mining methods presented so far handle large data sets having a small number of dimensions. However, some applications may need to mine high-dimensional data (i.e., data with hundreds or thousands of dimensions). Can we use the methods studied so far to mine high-dimensional data? The answer is unfortunately negative because the search spaces of such typical methods grow exponentially with the number of dimensions.
Researchers have overcome this difficulty in two directions. One direction extends a pattern growth approach by further exploring the vertical data format to handle data sets with a large number of dimensions (also called features or items, e.g., genes) but a small number of rows (also called transactions or tuples, e.g., samples). This is useful in applications like the analysis of gene expressions in bioinformatics, for example, where we often need to analyze microarray data that contain a large number of genes (e.g., 10,000 to 100,000) but only a small number of samples (e.g., 100 to 1000). The other direction develops a new mining methodology, called Pattern-Fusion, which mines colossal patterns, that is, patterns of very long length.
Let’s first briefly examine the first direction, in particular, a pattern growth–based row enumeration approach. Its general philosophy is to explore the vertical data format, as described in Section 6.2.5, which is also known as row enumeration. Row enumeration differs from traditional column (i.e., item) enumeration (also known as the horizontal data format). In traditional column enumeration, the data set, D, is viewed as a set of rows, where each row consists of an itemset. In row enumeration, the data set is instead viewed as an itemset, each consisting of a set of row_IDs indicating where the item appears in the traditional view of D. The original data set, D, can easily be transformed into a transposed data set, T. A data set with a small number of rows but a large number of dimensions is then transformed into a transposed data set with a large number of rows but a small number of dimensions. Efficient pattern growth methods can then be developed on such relatively low-dimensional data sets. The details of such an approach are left as an exercise for interested readers.
The remainder of this section focuses on the second direction. We introduce Pattern-Fusion, a new mining methodology that mines colossal patterns (i.e., patterns of very long length). This method takes leaps in the pattern search space, leading to a good approximation of the complete set of colossal frequent patterns.
7.4.1 Mining Colossal Patterns by Pattern-Fusion
Although we have studied methods for mining frequent patterns in various situations, many applications have hidden patterns that are tough to mine, due mainly to their immense length or size. Consider bioinformatics, for example, where a common activity is DNA or microarray data analysis. This involves mapping and analyzing very long DNA and protein sequences. Researchers are more interested in finding large patterns (e.g., long sequences) than finding small ones since larger patterns usually carry more significant meaning. We call these large patterns colossal patterns, as distinguished from patterns with large support sets. Finding colossal patterns is challenging because incremental mining tends to get “trapped” by an explosive number of midsize patterns before it can even reach candidate patterns of large size. This is illustrated in Example 7.10.
Example 7.10
The challenge of mining colossal patterns
Consider a 40 × 40 square table where each row contains the integers 1 through 40 in increasing order. Remove the integers on the diagonal, and this gives a 40 × 39 table. Add 20 identical rows to the bottom of the table, where each row contains the integers 41 through 79 in increasing order, resulting in a 60 × 39 table (Figure 7.6). We consider each row as a transaction and set the minimum support threshold at 20. The table has an exponential number (i.e., 
) of midsize closed/maximal frequent patterns of size 20, but only one that is colossal: 
of size 39. None of the frequent pattern mining algorithms that we have introduced so far can complete execution in a reasonable amount of time. The pattern search space is similar to that in Figure 7.7, where midsize patterns largely outnumber colossal patterns.
All of the pattern mining strategies we have studied so far, such as Apriori and FP-growth, use an incremental growth strategy by nature, that is, they increase the length of candidate patterns by one at a time. Breadth-first search methods like Apriori cannot bypass the generation of an explosive number of midsize patterns generated, making it impossible to reach colossal patterns. Even depth-first search methods like FP-growth can be easily trapped in a huge amount of subtrees before reaching colossal patterns. Clearly, a completely new mining methodology is needed to overcome such a hurdle.
A new mining strategy called Pattern-Fusion was developed, which fuses a small number of shorter frequent patterns into colossal pattern candidates. It thereby takes leaps in the pattern search space and avoids the pitfalls of both breadth-first and depth-first searches. This method finds a good approximation to the complete set of colossal frequent patterns.
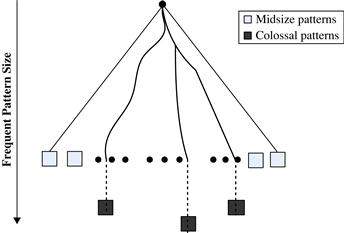
The Pattern-Fusion method has the following major characteristics. First, it traverses the tree in a bounded-breadth way. Only a fixed number of patterns in a bounded-size candidate pool are used as starting nodes to search downward in the pattern tree. As such, it avoids the problem of exponential search space.
Second, Pattern-Fusion has the capability to identify “shortcuts” whenever possible. Each pattern’s growth is not performed with one-item addition, but with an agglomeration of multiple patterns in the pool. These shortcuts direct Pattern-Fusion much more rapidly down the search tree toward the colossal patterns. Figure 7.8 conceptualizes this mining model.
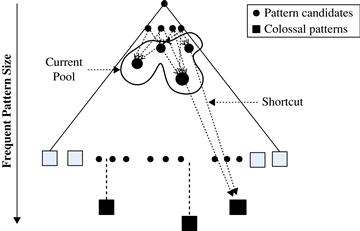
Figure 7.8 Pattern tree traversal: Candidates are taken froma pool of patterns, which results in shortcuts through pattern space to the colossal patterns.
As Pattern-Fusion is designed to give an approximation to the colossal patterns, a quality evaluation model is introduced to assess the patterns returned by the algorithm. An empirical study verifies that Pattern-Fusion is able to efficiently return high-quality results.
Let’s examine the Pattern-Fusion method in more detail. First, we introduce the concept of core pattern. For a pattern α, an itemset β ⊆ α is said to be a τ-core pattern of α if 
, 0 < τ ≤ 1, where |Dα| is the number of patterns containing α in database D. τ is called the core ratio. A pattern α is (d, τ)-robust if d is the maximum number of items that can be removed from α for the resulting pattern to remain a τ-core pattern of α, that is,
Example 7.11
Core patterns
Figure 7.9 shows a simple transaction database of four distinct transactions, each with 100 duplicates: 
. If we set τ = 0.5, then (ab) is a core pattern of α1 because (ab) is contained only by α1 and α4. Therefore, 
. α1 is (2, 0.5)-robust while α4 is (4, 0.5)-robust. The table also shows that larger patterns (e.g., (abcfe)) have far more core patterns than smaller ones (e.g., (bcf)).
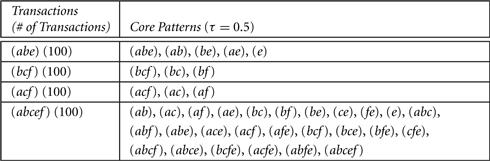
Figure 7.9 A transaction database, which contains duplicates, and core patterns for each distinct transaction.
From Example 7.11, we can deduce that large or colossal patterns have far more core patterns than smaller patterns do. Thus, a colossal pattern is more robust in the sense that if a small number of items are removed from the pattern, the resulting pattern would have a similar support set. The larger the pattern size, the more prominent this robustness. Such a robustness relationship between a colossal pattern and its corresponding core patterns can be extended to multiple levels. The lower-level core patterns of a colossal pattern are called core descendants.
Given a small c, a colossal pattern usually has far more core descendants of size c than a smaller pattern. This means that if we were to draw randomly from the complete set of patterns of size c, we would be more likely to pick a core descendant of a colossal pattern than that of a smaller pattern. In Figure 7.9, consider the complete set of patterns of size c = 2, which contains 
patterns in total. For illustrative purposes, let’s assume that the larger pattern, abcef, is colossal. The probability of being able to randomly draw a core descendant of abcef is 0.9. Contrast this to the probability of randomly drawing a core descendent of smaller (noncolossal) patterns, which is at most 0.3. Therefore, a colossal pattern can be generated by merging a proper set of its core patterns. For instance, abcef can be generated by merging just two of its core patterns, ab and cef, instead of having to merge all of its 26 core patterns.
Now, let’s see how these observations can help us leap through pattern space more directly toward colossal patterns. Consider the following scheme. First, generate a complete set of frequent patterns up to a user-specified small size, and then randomly pick a pattern, β. β will have a high probability of being a core-descendant of some colossal pattern, α. Identify all of α’s core-descendants in this complete set, and merge them. This generates a much larger core-descendant of α, giving us the ability to leap along a path toward α in the core-pattern tree, Tα. In the same fashion we select K patterns. The set of larger core-descendants generated is the candidate pool for the next iteration.
A question arises: Given β, a core-descendant of a colossal pattern α, how can we find the other core-descendants of α? Given two patterns, α and β, the pattern distance between them is defined as 
. Pattern distance satisfies the triangle inequality.
For a pattern, α, let Cα be the set of all its core patterns. It can be shown that Cα is bounded in metric space by a “ball” of diameter r(τ), where 
. This means that given a core pattern β ∈ Cα, we can identify all of α’s core patterns in the current pool by posing a range query. Note that in the mining algorithm, each randomly drawn pattern could be a core-descendant of more than one colossal pattern, and as such, when merging the patterns found by the “ball,” more than one larger core-descendant could be generated.
From this discussion, the Pattern-Fusion method is outlined in the following two phases:
1. Initial Pool: Pattern-Fusion assumes an initial pool of small frequent patterns is available. This is the complete set of frequent patterns up to a small size (e.g., 3). This initial pool can be mined with any existing efficient mining algorithm.
2. Iterative Pattern-Fusion: Pattern-Fusion takes as input a user-specified parameter, K, which is the maximum number of patterns to be mined. The mining process is iterative. At each iteration, K seed patterns are randomly picked from the current pool. For each of these K seeds, we find all the patterns within a ball of a size specified by τ. All the patterns in each “ball” are then fused together to generate a set of superpatterns. These superpatterns form a new pool. If the pool contains more than K patterns, the next iteration begins with this pool for the new round of random drawing. As the support set of every superpattern shrinks with each new iteration, the iteration process terminates.
Note that Pattern-Fusion merges small subpatterns of a large pattern instead of incrementally-expanding patterns with single items. This gives the method an advantage to circumvent midsize patterns and progress on a path leading to a potential colossal pattern. The idea is illustrated in Figure 7.10. Each point shown in the metric space represents a core pattern. In comparison to a smaller pattern, a larger pattern has far more core patterns that are close to one another, all of which are bounded by a ball, as shown by the dotted lines. When drawing randomly from the initial pattern pool, we have a much higher probability of getting a core pattern of a large pattern, because the ball of a larger pattern is much denser.
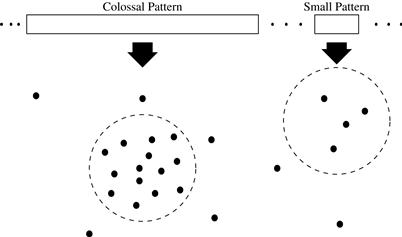
Figure 7.10 Pattern metric space: Each point represents a core pattern. The core patterns of a colossal pattern are denser than those of a small pattern, as shown within the dotted lines.
It has been theoretically shown that Pattern-Fusion leads to a good approximation of colossal patterns. The method was tested on synthetic and real data sets constructed from program tracing data and microarray data. Experiments show that the method can find most of the colossal patterns with high efficiency.