7.4 A Gallery of Solution Curves of Linear Systems
In the preceding section we saw that the eigenvalues and eigenvectors of the n×n
Indeed, according to Theorem 1 from Section 7.3, if λ
is a nontrivial solution of the system (1). Moreover, if A has n linearly independent eigenvectors v1, v2, …,
where c1,c2,…,cn
Our goal in this section is to gain a geometric understanding of the role that the eigenvalues and eigenvectors of the matrix A play in the solutions of the system (1). We will see, illustrating primarily with the case n=2,
Systems of Dimension n=2
Until stated otherwise, we henceforth assume that n=2,
if λ1
if λ1
as before. If A does not have two linearly independent eigenvectors, then—as we will see—we can find a vector v2
where v1
With this algebraic background in place, we begin our analysis of the solution curves of the system (1). First we assume that the eigenvalues λ1
Real Eigenvalues
We will divide the case where λ1
Distinct eigenvalues
Nonzero and of opposite sign (λ1<0<λ2
λ1<0<λ2 )Both negative (λ1<λ2<0
λ1<λ2<0 )Both positive (0<λ2<λ1
0<λ2<λ1 )One zero and one negative (λ1<λ2=0
λ1<λ2=0 )One zero and one positive (0=λ2<λ1
0=λ2<λ1 )
Repeated eigenvalue
Positive (λ1=λ2>0
λ1=λ2>0 )Negative (λ1=λ2<0
λ1=λ2<0 )Zero (λ1=λ2=0
λ1=λ2=0 )
Saddle Points
Nonzero Distinct Eigenvalues of Opposite Sign: The key observation when λ1<0<λ2
of the system x′=Ax
Geometrically, this means that all solution curves given by (4) with both c1

FIGURE 7.4.1.
Solution curves x(t)=c1v1eλ1t+c2v2eλ2t
If c1
Figure 7.4.1 illustrates typical solution curves corresponding to nonzero values of the coefficients c1
Example 1
The solution curves in Fig. 7.4.1 correspond to the choice
in the system x′=Ax
According to Eq. (4), the resulting general solution is
or, in scalar form,
Our gallery Fig. 7.4.16 at the end of this section shows a more complete set of solution curves, together with a direction field, for the system x′=Ax
Nodes: Sinks and Sources
Distinct Negative Eigenvalues: When λ1<λ2<0,
approaches the origin; likewise, as t→−∞,
This shows that the tangent vector x′(t)
If c2=0,

FIGURE 7.4.2.
Solution curves x(t)=c1v1eλ1t+c2v2eλ2t
To describe the appearance of phase portraits like Fig. 7.4.2, we introduce some new terminology, which will be useful both now and in Chapter 9, when we study nonlinear systems. In general, we call the origin a node of the system x′=Ax
Either every trajectory approaches the origin as t→+∞
t→+∞ or every trajectory recedes from the origin as t→+∞t→+∞ ;Every trajectory is tangent at the origin to some straight line through the origin.
Moreover, we say that the origin is a proper node provided that no two different pairs of “opposite” trajectories are tangent to the same straight line through the origin. This is the situation in Fig. 7.4.6, in which the trajectories are straight lines, not merely tangent to straight lines;indeed, a proper node might be called a “star point.” However, in Fig. 7.4.2, all trajectories—apart from those that flow along the line l1
Further, if every trajectory for the system x′=Ax
Example 2
The solution curves in Fig. 7.4.2 correspond to the choice
in the system x′=Ax.
Equation (4) then gives the general solution
or, in scalar form,
Our gallery Fig. 7.4.16 shows a more complete set of solution curves, together with a direction field, for the system x′=Ax
The case of distinct positive eigenvalues mirrors that of distinct negative eigenvalues. But instead of analyzing it independently, we can rely on the following principle, whose verification is a routine matter of checking signs (Problem 30).
We note furthermore that the two vector-valued functions x(t) and ~x(t)
Distinct Positive Eigenvalues: If the matrix A has positive eigenvalues with 0<λ2<λ1,

FIGURE 7.4.3.
Solution curves x(t)=c1v1eλ1t+c2v2eλ2t for the system x′=Ax when the eigenvalues λ1,λ2 of A are real with 0<λ2<λ1.
Example 3
The solution curves in Fig. 7.4.3 correspond to the choice
in the system x′=Ax; thus A is the negative of the matrix in Example 2. Therefore we can solve the system x′=Ax by applying the principle of time reversal to the solution in Eq. (13): Replacing t with −t in the righthand side of (13) leads to
Of course, we could also have “started from scratch” by finding the eigenvalues λ1, λ2 and eigenvectors v1, v2 of A. These can be found from the definition of eigenvalue, but it is easier to note (see Problem 31 again)that because A is the negative of the matrix in Eq. (12), λ1 and λ2 are likewise the negatives of their values in Example 2, whereas we can take v1 and v2 to be the same as in Example 2. By either means we find that λ1=14 and λ2=7 (so that 0<λ2<λ1), with associated eigenvectors
From Eq. (4), then, the general solution is
(in agreement with Eq. (16)), or, in scalar form,
Our gallery Fig. 7.4.16 shows a more complete set of solution curves, together with a direction field, for the system x′=Ax with A given by Eq. (15).
Zero Eigenvalues and Straight-Line Solutions
One Zero and One Negative Eigenvalue: When λ1<λ2=0, the general solution (4) becomes
For any fixed nonzero value of the coefficient c1, the term c1v1eλ1t in Eq. (17) is a scalar multiple of the eigenvector v1, and thus (as t varies) travels along the line l1 passing through the origin and parallel to v1; the direction of travel is toward the origin as t→+∞ because λ1<0. If c1>0, for example, then c1v1eλ1t extends in the direction of v1, approaching the origin as t increases, and receding from the origin as t decreases. If instead c1<0, then c1v1eλ1t extends in the direction opposite v1 while still approaching the origin as t increases. Loosely speaking, we can visualize the flow of the term c1v1eλ1t taken alone as a pair of arrows opposing each other head-to-head at the origin. The solution curve x(t) in Eq. (17) is simply this same trajectory c1v1eλ1t, then shifted (or offset) by the constant vector c2v2. Thus in this case the phase portrait of the system x′=Ax consists of all lines parallel to the eigenvector v1, where along each such line the solution flows (from both directions) toward the line l2 passing through the origin and parallel to v1. Figure 7.4.4 illustrates typical solution curves corresponding to nonzero values of the coefficients c1 and c2.

FIGURE 7.4.4.
Solution curves x(t)=c1v1eλ1t+c2v2eλ2t for the system x′=Ax when the eigenvalues λ1,λ2 of A are real with λ1<λ2=0.
It is noteworthy that each single point represented by a constant vector b lying on the line l2 represents a constant solution of the system x′=Ax. Indeed, if b lies on l2, then b is a scalar multiple k·v2 of the eigenvector v2 of A associated with the eigenvalue λ2=0. In this case, the constant-valued solution x(t)≡b is given by Eq. (17) with c1=0 and c2=k. This constant solution, with its “trajectory” being a single point lying on the line l2, is then the unique solution of the initial value problem
guaranteed by Theorem 1 of Section 7.1. Note that this situation is in marked contrast with the other eigenvalue cases we have considered so far, in which x(t)≡0 is the only constant solution of the system x′=Ax. (In Problem 32 we explore the general circumstances under which the system x′=Ax has constant solutions other than x(t)≡0.)
Example 4
The solution curves in Fig. 7.4.4 correspond to the choice
in the system x′=Ax. The eigenvalues of A are λ1=−35 and λ2=0, with associated eigenvectors
Based on Eq. (17), the general solution is
or, in scalar form,
Our gallery Fig. 7.4.16 shows a more complete set of solution curves, together with a direction field, for the system x′=Ax with A given by Eq. (18).
One Zero and One Positive Eigenvalue: When 0=λ2<λ1, the solution of the system x′=Ax is again given by
By the principle of time reversal, the trajectories of the system x′=Ax are identical to those of the system x′=−Ax, except that they flow in the opposite direction. Since the eigenvalues −λ1 and −λ2 of the matrix −A satisfy −λ1<−λ2=0, by the preceding case the trajectories of x′=−Ax are lines parallel to the eigenvector v1 and flowing toward the line l2 from both directions. Therefore the trajectories of the system x′=Ax are lines parallel to v1 and flowing away from the line l2. Figure 7.4.5 illustrates typical solution curves given by x(t)=c1v1eλ1t+c2v2 corresponding to nonzero values of the coefficients c1 and c2.

FIGURE 7.4.5.
Solution curves x(t)=c1v1eλ1t+c2v2eλ2t for the system x′=Ax when the eigenvalues λ1,λ2 of A are real with 0=λ2<λ1.
Example 5
The solution curves in Fig. 7.4.5 correspond to the choice
in the system x′=Ax; thus A is the negative of the matrix in Example 4. Once again we can solve the system using the principle of time reversal:Replacing t with −t in the right-hand side of the solution in Eq. (19) of Example 4 leads to
Alternatively, directly finding the eigenvalues and eigenvectors of A leads to λ1=35 and λ2=0, with associated eigenvectors
Equation (17) gives the general solution of the system x′=Ax as
(in agreement with Eq. (21)), or, in scalar form,
Our gallery Fig.7.4.16 shows a more complete set of solution curves, together with a direction field, for the system x′=Ax with A given by Eq. (20).
Repeated Eigenvalues; Proper and Improper Nodes
Repeated Positive Eigenvalue: As we noted earlier, if the matrix A has one repeated eigenvalue, then A may or may not have two associated linearly independent eigenvectors. Because these two possibilities lead to quite different phase portraits, we will consider them separately. We let λ denote the repeated eigenvalue of A with λ>0.
With two independent eigenvectors: First, if A does have two linearly independent eigenvectors, then it is easy to show (Problem 33) that in fact every nonzero vector is an eigenvector of A, from which it follows that A must be equal to the scalar λ times the identity matrix of order two, that is,
Therefore the system x′=Ax becomes (in scalar form)
The general solution of Eq. (23) is
or in vector format,
We could also have arrived at Eq. (25) by starting, as in previous cases, from our general solution (4): Because all nonzero vectors are eigenvectors of A, we are free to take v1=[10]T and v2=[01]T as a representative pair of linearly independent eigenvectors, each associated with the eigenvalue λ. Then Eq. (4) leads to the same result as Eq. (25):
Either way, our solution in Eq. (25) shows that x(t) is always a positive scalar multiple of the fixed vector [c1c2]T. Thus apart from the case c1=c2=0, the trajectories of the system (1) are half-lines, or rays, emanating from the origin and (because λ>0) flowing away from it. As noted above, the origin in this case represents a proper node, because no two pairs of “opposite” solution curves are tangent to the same straight line through the origin. Moreover the origin is also a source (rather than a sink), and so in this case we call the origin a proper nodal source. Figure 7.4.6 shows the “exploding star” pattern characteristic of such points.
Example 6
The solution curves in Fig.7.4.6 correspond to the case where the matrix A is given by Eq. (22) with λ=2:

FIGURE 7.4.6.
Solution curves x(t)=eλt[c1c2] for the system x′=Ax when A has one repeated positive eigenvalue and two linearly independent eigenvectors.
Equation (25) then gives the general solution of the system x′=Ax as
or, in scalar form,
Our gallery Fig. 7.4.16 shows a more complete set of solution curves, together with a direction field, for the system x′=Ax with A given by Eq. (26).
Without two independent eigenvectors: The remaining possibility is that the matrix A has a repeated positive eigenvalue yet fails to have two linearly independent eigenvectors. In this event the general solution of the system x′=Ax is given by Eq. (7) above:
Here v1 is an eigenvector of the matrix A associated with the repeated eigenvalue λ and v2 is a (nonzero) “generalized eigenvector” that will be described more fully in Section 7.6. To analyze this trajectory, we first distribute the factor eλt in Eq. (7), leading to
Our assumption that λ>0 implies that both eλt and teλt approach zero as t→−∞, and so by Eq. (28) the solution x(t) approaches the origin as t→−∞. Except for the trivial solution given by c1=c2=0, all trajectories given by Eq. (7) “emanate” from the origin as t increases.
The direction of flow of these curves can be understood from the tangent vector x′(t). Rewriting Eq. (28) as
and applying the product rule for vector-valued functions gives
For t≠0, we can factor out t in Eq. (29) and rearrange terms to get
Equation (30) shows that for t≠0, the tangent vector x′(t) is a nonzero scalar multiple of the vector λc2v1+1t(λc1v1+λc2v2+c2v1), which, if c2≠0, approaches the fixed nonzero multiple λc2v1 of the eigenvector v1 as t→+∞ or as t→−∞. In this case it follows that as t gets larger and larger numerically (in either direction), the tangent line to the solution curve at the point x(t)—since it is parallel to the tangent vector x′(t) which approaches λc2v1—becomes more and more nearly parallel to the eigenvector v1. In short, we might say that as t increases numerically, the point x(t) on the solution curve moves in a direction that is more and more nearly parallel to the vector v1, or still more briefly, that near x(t) the solution curve itself is virtually parallel to v1.
We conclude that if c2≠0, then as t→−∞ the point x(t) approaches the origin along the solution curve which is tangent there to the vector v1. But as t→+∞ and the point x(t) recedes farther and farther from the origin, the tangent line to the trajectory at this point tends to differ (in direction) less and less from the (moving) line through x(t) that is parallel to the (fixed) vector v1. Speaking loosely but suggestively, we might therefore say that at points sufficiently far from the origin, all trajectories are essentially parallel to the single vector v1.
If instead c2=0, then our solution (7) becomes
and thus runs along the line l1 passing through the origin and parallel to the eigenvector v1. Because λ>0, x(t) flows away from the origin as t increases; the flow is in the direction of v1 if c1>0, and opposite v1 if c1<0.
We can further see the influence of the coefficient c2 by writing Eq. (7) in yet a different way:
It follows from Eq. (32) that if c2≠0, then the solution curve x(t) does not cross the line l1. Indeed, if c2>0, then Eq. (32) shows that for all t, the solution curve x(t) lies on the same side of l1 as v2, whereas if c2<0, then x(t) lies on the opposite side of l1.
To see the overall picture, then, suppose for example that the coefficient c2>0. Starting from a large negative value of t, Eq. (30) shows that as t increases, the direction in which the solution curve x(t) initially proceeds from the origin is roughly that of the vector teλtλc2v1. Since the scalar teλtλc2 is negative (because t<0 and λc2>0), the direction of the trajectory is opposite that of v1. For large positive values of t, on the other hand, the scalar teλtλc2 is positive, and so x(t) flows in nearly the same direction as v1. Thus, as t increases from −∞ to +∞, the solution curve leaves the origin flowing in the direction opposite v1, makes a “U-turn” as it moves away from the origin, and ultimately flows in the direction of v1.
Because all nonzero trajectories are tangent at the origin to the line l1, the origin represents an improper nodal source. Figure 7.4.7 illustrates typical solution curves given by x(t)=c1v1eλt+c2(v1t+v2)eλt for the system x′=Ax when A has a repeated eigenvalue but does not have two linearly independent eigenvectors.

FIGURE 7.4.7.
Solution curves x(t)=c1v1eλt+c2(v1t+v2)eλt for the system x′=Ax when A has one repeated positive eigenvalue λ with associated eigenvector v1 and “generalized eigenvector” v2.
Example 7
The solution curves in Fig. 7.4.7 correspond to the choice
in the system x′=Ax. In Examples 2 and 3 of Section 7.6 we will see that A has the repeated eigenvalue λ=4 with associated eigenvector and generalized eigenvector given by
respectively. According to Eq. (7) the resulting general solution is
or, in scalar form,
Our gallery Fig. 7.4.16 shows a more complete set of solution curves, together with a direction field, for the system x′=Ax with A given by Eq. (33).
Repeated Negative Eigenvalue: Once again the principle of time reversal shows that the solutions x(t) of the system x′=Ax are identical to those of x′=−Ax with t replaced by −t; hence these two systems share the same trajectories while flowing in opposite directions. Further, if the matrix A has the repeated negative eigenvalue λ, then the matrix −A has the repeated positive eigenvalue −λ (Problem 31 again). Therefore, to construct phase portraits for the system x′=Ax when A has a repeated negative eigenvalue, we simply reverse the directions of the trajectories in the phase portraits corresponding to a repeated positive eigenvalue. These portraits are illustrated in Figs. 7.4.8 and 7.4.9. In Fig. 7.4.8 the origin represents a proper nodal sink, whereas in Fig. 7.4.9 it represents an improper nodal sink.

FIGURE 7.4.8.
Solution curves x(t)=eλt[c1c2] for the system x′=Ax when A has one repeated negative eigenvalue λ and two linearly independent eigenvectors.

FIGURE 7.4.9.
Solution curves x(t)=c1v1eλt+c2(v1t+v2)eλt for the system x′=Ax when A has one repeated negative eigenvalue λ with associated eigenvector v1 and “generalized eigenvector” v2.
Example 8
The solution curves in Fig. 7.4.8 correspond to the choice
in the system x′=Ax; thus A is the negative of the matrix in Example 6. We can solve this system by applying the principle of time reversal to the solution found in Eq. (27): Replacing t with −t in the right-hand side of Eq. (27) leads to
or, in scalar form,
Alternatively, because A is given by Eq. (22) with λ=−2, Eq. (25) leads directly to the solution in Eq. (37). Our gallery Fig. 7.4.16 shows a more complete set of solution curves, together with a direction field, for the system x′=Ax with A given by Eq. (36).
Example 9
The solution curves in Fig. 7.4.9 correspond to the choice
in the system x′=Ax. Thus A is the negative of the matrix in Example 7, and once again we can apply the principle of time reversal to the solution found in Eq. (35): Replacing t with −t in the right-hand side of Eq. (35) yields
We could also arrive at an equivalent form of the solution in Eq. (39) in the following way. You can verify that A has the repeated eigenvalue λ=−2 with eigenvector v1 given by Eq. (34), that is,
However, as the methods of Section 7.6 will show, a generalized eigenvector v2 associated with v1 is now given by
that is, v2 is the negative of the generalized eigenvector in Eq. (34). Equation (7) then gives the general solution of the system x′=Ax as
or, in scalar form,
Note that replacing c2 with −c2 in the solution (39) yields the solution (40), thus confirming that the two solutions are indeed equivalent. Our gallery Fig. 7.4.16 shows a more complete set of solution curves, together with a direction field, for the system x′=Ax with A given by Eq. (38).
The Special Case of a Repeated Zero Eigenvalue
Repeated Zero Eigenvalue: Once again the matrix A may or may not have two linearly independent eigenvectors associated with the repeated eigenvalue λ=0. If it does, then (using Problem 33 once more)we conclude that every nonzero vector is an eigenvector of A, that is, that Av=0·v=0 for all two-dimensional vectors v. It follows that A is the zero matrix of order two, that is,
Therefore the system x′=Ax reduces to x′1(t)=x′2(t)=0, which is to say that x1(t) and x2(t) are each constant functions. Thus the general solution of x′=Ax is simply
where c1 and c2 are arbitrary constants, and the “trajectories” given by Eq. (41) are simply the fixed points (c1,c2) in the phase plane.
If instead A does not have two linearly independent eigenvectors associated with λ=0, then the general solution of the system x′=Ax is given by Eq. (7) with λ=0:
Once again v1 denotes an eigenvector of the matrix A associated with the repeated eigenvalue λ=0 and v2 denotes a corresponding nonzero “generalized eigenvector.” If c2≠0, then the trajectories given by Eq. (42) are lines parallel to the eigenvector v1 and “starting” at the point c1v1+c2v2 (when t=0). When c2>0 the trajectory proceeds in the same direction as v1, whereas when c2<0 the solution curve flows in the direction opposite v1. Once again the lines l1 and l2 passing through the origin and parallel to the vectors v1 and v2, respectively, divide the plane into “quadrants” corresponding to the signs of the coefficients c1 and c2. The particular quadrant in which the “starting point” c1v1+c2v2 of the trajectory falls is determined by the signs of c1 and c2. Finally, if c2=0, then Eq. (42) gives x(t)≡c1v1 for all t, which means that each fixed point c1v1 along the line l1 corresponds to a solution curve. (Thus the line l1 could be thought of as a median strip dividing two opposing lanes of traffic.) Figure 7.4.10 illustrates typical solution curves corresponding to nonzero values of the coefficients c1 and c2.

FIGURE 7.4.10.
Solution curves x(t)=(c1v1+c2v2)+c2v1t for the system x′=Ax when A has a repeated zero eigenvalue with associated eigenvector v1 and “generalized eigenvector” v2. The emphasized point on each solution curve corresponds to t=0.
Example 10
The solution curves in Fig. 7.4.10 correspond to the choice
in the system x′=Ax. You can verify that v1=[2−1]T is an eigenvector of A associated with the repeated eigenvalue λ=0. Further, using the methods of Section 7.6 we can show that v2=[10]T is a corresponding “generalized eigenvector” of A. According to Eq. (42) the general solution of the system x′=Ax is therefore
or, in scalar form,
Our gallery Fig.7.4.16 shows a more complete set of solution curves, together with a direction field, for the system x′=Ax with A given by Eq. (43).
Complex Conjugate Eigenvalues and Eigenvectors
We turn now to the situation in which the eigenvalues λ1 and λ2 of the matrix A are complex conjugate. As we noted at the beginning of this section, the general solution of the system x′=Ax is given by Eq. (5):
Here the vectors a and b are the real and imaginary parts, respectively, of a (complex-valued) eigenvector of A associated with the eigenvalue λ1=p+iq. We will divide the case of complex conjugate eigenvalues according to whether the real part p of λ1 and λ2 is zero, positive, or negative:
Pure imaginary (λ1, λ2=±iq with q≠0)
Complex with negative real part (λ1, λ2=p±iq with p<0 and q≠0)
Complex with positive real part (λ1, λ2=p±iq with p>0 and q≠0)
Pure Imaginary Eigenvalues: Centers and Elliptical Orbits
Pure Imaginary Eigenvalues: Centers and Elliptical Orbits Here we assume that the eigenvalues of the matrix A are given by λ1 λ2=±iq with q≠0. Taking p=0 in Eq. (5) gives the general solution
for the system x′=Ax. Rather than directly analyze the trajectories given by Eq. (45), as we have done in the previous cases, we begin instead with an example that will shed light on the nature of these solution curves.
Example 11
Solve the initial value problem
Solution
The coefficient matrix
has characteristic equation
and hence has the complex conjugate eigenvalues λ1, λ2=±10i. If v=[ab]T is an eigenvector associated with λ=10i, then the eigenvector equation (A−λI)v=0 yields
Upon division of the second row by 2, this gives the two scalar equations
each of which is satisfied by a=3+5i and b=4. Thus the desired eigenvector is v=[3+5i4]T, with real and imaginary parts
respectively. Taking q=10 in Eq. (45) therefore gives the general solution of the system x′=Ax:
To solve the given initial value problem it remains only to determine values of the coefficients c1 and c2. The initial condition x(0)=[42]T readily yields c1=c2=12, and with these values Eq. (50) becomes (in scalar form)
Figure 7.4.11 shows the trajectory given by Eq. (51) together with the initial point (4, 2).
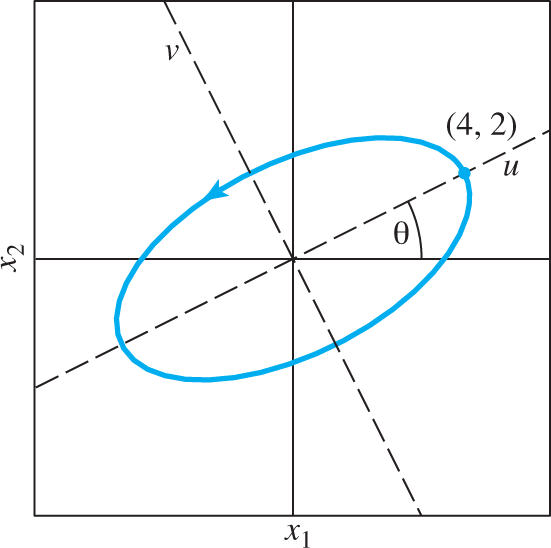
FIGURE 7.4.11.
Solution curve x1(t)=4cos10t−sin10t,x2(t)=2cos10t+2sin10t for the initial value problem in Eq. (46).
This solution curve appears to be an ellipse rotated counterclockwise by the angle θ=arctan24≈0.4636. We can verify this by finding the equations of the solution curve relative to the rotated u- and v-axes shown in Fig. 7.4.11. By a standard formula from analytic geometry, these new equations are given by
In Problem 34 we ask you to substitute the expressions for x1 and x2 from Eq. (51) into Eq. (52), leading (after simplification) to
Equation (53) not only confirms that the solution curve in Eq. (51) is indeed an ellipse rotated by the angle θ, but it also shows that the lengths of the semi-major and semi-minor axes of the ellipse are 2√5 and √5, respectively.
Furthermore, we can demonstrate that any choice of initial point (apart from the origin) leads to a solution curve that is an ellipse rotated by the same angle θ and “concentric” (in an obvious sense) with the trajectory in Fig.7.4.11 (see Problems 35–37). All these concentric rotated ellipses are centered at the origin (0, 0), which is therefore called a center for the system x′=Ax whose coefficient matrix A has pure imaginary eigenvalues. Our gallery Fig.7.4.16 shows a more complete set of solution curves, together with a direction field, for the system x′=Ax with A given by Eq. (47).
Further investigation: Geometric significance of the eigenvector. Our general solution in Eq. (50) was based upon the vectors a and b in Eq. (49), that is, the real and imaginary parts of the complex eigenvector v=[3+5i4]T of the matrix A. We might therefore expect a and b to have some clear geometric connection to the solution curve in Fig. 7.4.11. For example, we might guess that a and b would be parallel to the major and minor axes of the elliptical trajectory. However, it is clear from Fig. 7.4.12—which shows the vectors a and b together with the solution curve given by Eq. (51)—that this is not the case. Do the eigenvectors of A, then, play any geometric role in the phase portrait of the system x′=Ax?

FIGURE 7.4.12.
Solution curve for the initial value problem in Eq. (46) showing the vectors a, b, ˜a, and ˜b.
The (affirmative) answer lies in the fact that any nonzero real or complex multiple of a complex eigenvector of the matrix A is still an eigenvector of A associated with that eigenvalue. Perhaps, then, if we multiply the eigenvector v=[3+5i4]T by a suitable nonzero complex constant z, the resulting eigenvector ~v will have real and imaginary parts ~a and ~b that can be readily identified with geometric features of the ellipse. To this end, let us multiply v by the complex scalar z=12(1+i). (The reason for this particular choice will become clear shortly.)The resulting new complex eigenvector ~v of the matrix A is,
and has real and imaginary parts
It is clear that the vector ~b is parallel to the major axis of our elliptical trajectory. Further, you can easily check that ~a·~b=0, which means that ~a is perpendicular to ~b, and hence is parallel to the minor axis of the ellipse, as Fig. 7.4.12 illustrates. Moreover, the length of ~b is twice that of ~a, reflecting the fact that the lengths of the major and minor axes of the ellipse are in this same ratio. Thus for a matrix A with pure imaginary eigenvalues, the complex eigenvector of A used in the general solution (45)—if suitably chosen—is indeed of great significance to the geometry of the elliptical solution curves of the system x′=Ax.
How was the value 12(1+i) chosen for the scalar z? In order that the real and imaginary parts ~a and ~b of ~v=z·v be parallel to the axes of the ellipse, at a minimum ~a and ~b must be perpendicular to each other. In Problem 38 we ask you to show that this condition is satisfied if and only if z is of the form r(1±i), where r is a nonzero real number, and that if z is chosen in this way, then ~a and ~b are in fact parallel to the axes of the ellipse. The value r=12 then aligns the lengths of ~a and ~b with those of the semi-minor and -major axes of the elliptical trajectory. More generally, we can show that given any eigenvector v of a matrix A with pure imaginary eigenvalues, there exists a constant z such that the real and imaginary parts ~a and ~b of the eigenvector ~v=z·v are parallel to the axes of the (elliptical) trajectories of the system x′=Ax.
Further investigation: Direction of flow. Figs. 7.4.11 and 7.4.12 suggest that the solution curve in Eq. (51) flows in a counterclockwise direction with increasing t. However, you can check that the matrix
has the same eigenvalues and eigenvectors as the matrix A in Eq. (47) itself, and yet (by the principle of time reversal) the trajectories of the system x′=−Ax are identical to those of x′=Ax while flowing in the opposite direction, that is, clockwise. Clearly, mere knowledge of the eigenvalues and eigenvectors of the matrix A is not sufficient to predict the direction of flow of the elliptical trajectories of the system x′=Ax as t increases. How then can we determine this direction of flow?
One simple approach is to use the tangent vector x′ to monitor the direction in which the solution curves flow as they cross the positive x1-axis. If s is any positive number (so that the point (s, 0) lies on the positive x1-axis), and if the matrix A is given by
then any trajectory for the system x′=Ax passing through (s, 0) satisfies
at the point (s, 0). Therefore, at this point the direction of flow of the solution curve is a positive scalar multiple of the vector [ac]T. Since c cannot be zero (see Problem 39), this vector either points “upward” into the first quadrant of the phase plane (if c>0 ), or “downward” into the fourth quadrant (if c<0). If upward, then the flow of the solution curve is counterclockwise; if downward, then clockwise. For the matrix A in Eq. (47), the vector [ac]T=[68]T points into the first quadrant because c=8>0, thus indicating a counterclockwise direction of flow (as Figs. 7.4.11 and 7.4.12 suggest).
Complex Eigenvalues: Spiral Sinks and Sources
Complex Eigenvalues with Negative Real Part: Now we assume that the eigenvalues of the matrix A are given by λ1, λ2=p±iq with q≠0 and p<0. In this case the general solution of the system x′=Ax is given directly by Eq. (5):
where the vectors a and b have their usual meaning. Once again we begin with an example to gain an understanding of these solution curves.
Example 12
Solve the initial value problem
Solution
The coefficient matrix
has characteristic equation
and hence has the complex conjugate eigenvalues λ1, λ2=−1±10i. If v=[ab]T is an eigenvector associated with λ=−1+10i, then the eigenvector equation (A−λI)v=0 yields the same system (48) of equations found in Example 11:
As in Example 11, each of these equations is satisfied by a=3+5i and b=4. Thus the desired eigenvector, associated with λ1=−1+10i, is once again v=[3+5i4]T, with real and imaginary parts
respectively. Taking p=−1 and q=10 in Eq. (5) therefore gives the general solution of the system x′=Ax:
The initial condition x(0)=[42]T gives c1=c2=12 once again, and with these values Eq. (57) becomes (in scalar form)
Figure 7.4.13 shows the trajectory given by Eq. (58) together with the initial point (4, 2). It is noteworthy to compare this spiral trajectory with the elliptical trajectory in Eq. (51). The equations for x1(t) and x2(t) in (58) are obtained by multiplying their counterparts in (51) by the common factor e−t, which is positive and decreasing with increasing t. Thus for positive values of t, the spiral trajectory is generated, so to speak, by standing at the origin and “reeling in” the point on the elliptical trajectory (51) as it is traced out. When t is negative, the picture is rather one of “casting away” the point on the ellipse farther out from the origin to create the corresponding point on the spiral.

FIGURE 7.4.13.
Solution curve x1(t)=e−t(4 cos 10t− sin 10t), x2(t)=e−t(2 cos 10t+2 sin 10t). for the initial value problem in Eq. (54). The dashed and solid portions of the curve correspond to negative and positive values of t, respectively.
Our gallery Fig. 7.4.16 shows a more complete set of solution curves, together with a direction field, for the system x′=Ax with A given by Eq. (55). Because the solution curves all “spiral into” the origin, we call the origin in this a case a spiral sink.
Complex Eigenvalues with Positive Real Part: We conclude with the case where the eigenvalues of the matrix A are given by λ1, λ2=p±iq with q≠0 and p>0. Just as in the preceding case, the general solution of the system x′=Ax is given by Eq. (5):
An example will illustrate the close relation between the cases p>0 and p<0.
Example 13
Solve the initial value problem
Solution
Although we could directly apply the eigenvalue/eigenvector method as in previous cases (see Problem 40), here it is more convenient to notice that the coefficient matrix
is the negative of the matrix in Eq. (55) used in Example 12. By the principle of time reversal, therefore, the solution of the initial value problem (59) is given by simply replacing t with −t in the right-hand sides of the solution (58) of the initial value problem in that example:
Figure 7.4.14 shows the trajectory given by Eq. (61) together with the initial point (4, 2). Our gallery Fig. 7.4.16 shows this solution curve together with a direction field for the system x′=Ax with A given by Eq. (60). Because the solution curve “spirals away from” the origin, we call the origin in this case a spiral source.

FIGURE 7.4.14.
Solution curve x1(t)=et(4 cos 10t+sin 10t), x2(t)=et(2 cos 10t−2 sin 10t) for the initial value problem in Eq. (59). The dashed and solid portions of the curve correspond to negative and positive values of t, respectively.
A 3-Dimensional Example
Figure 7.4.15 illustrates the space trajectories of solutions of the 3-dimensional system x′=Ax with constant coefficient matrix
To portray the motion in space of a point x(t) moving on a trajectory of this system, we can regard this trajectory as a necklace string on which colored beads are placed to mark its successive positions at fixed increments of time (so the point is moving fastest where the spacing between beads is greatest). In order to aid the eye in following the moving point’s progress, the size of the beads decreases continuously with the passage of time and motion along the trajectory.

FIGURE 7.4.15.
Three-dimensional trajectories for the system x′=Ax with the matrix A given by Eq. (62).
The matrix A has the single real eigenvalue −1 with the single (real) eigenvector [001]T and the complex conjugate eigenvalues −1±5i. The negative real eigenvalue corresponds to trajectories that lie on the x3-axis and approach the origin as t→0 (as illustrated by the beads on the vertical axis of the figure). Thus the origin (0, 0, 0) is a sink that “attracts” all the trajectories of the system.
The complex conjugate eigenvalues with negative real part correspond to trajectories in the horizontal x1x2-plane that spiral around the origin while approaching it. Any other trajectory—one which starts at a point lying neither on the z-axis nor in the x1x2-plane—combines the preceding behaviors by spiraling around the surface of a cone while approaching the origin at its vertex.
Gallery of Typical Phase Portraits for the System x′=Ax: Nodes
FIGURE 7.4.16.
Gallery of typical phase plane portraits for the system x′=Ax.
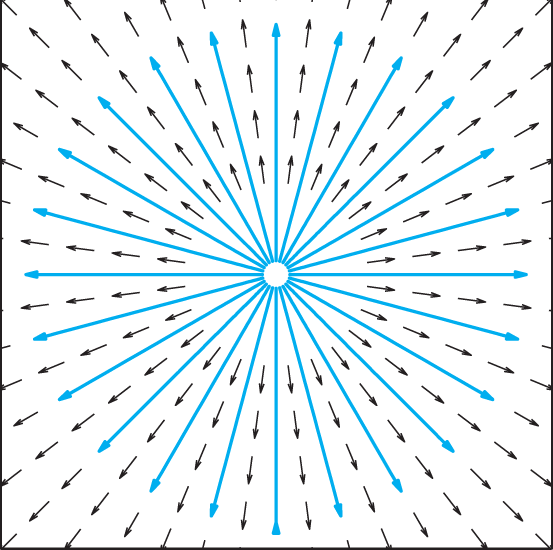
Proper Nodal Source: A repeated positive real eigenvalue with two linearly independent eigenvectors.

Proper Nodal Sink: A repeated negative real eigenvalue with two linearly independent eigenvectors.

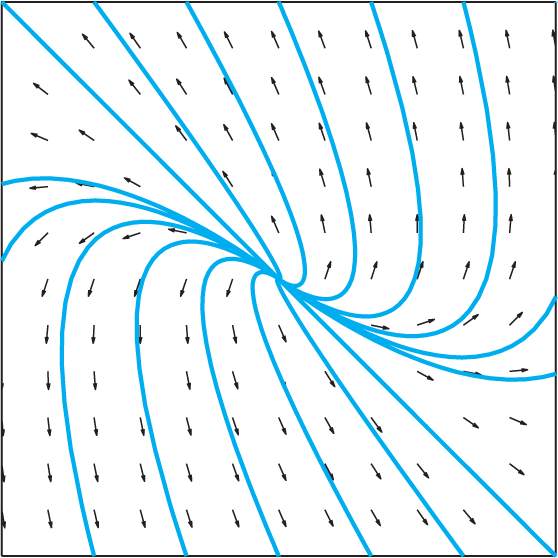
Improper Nodal Source: Distinct positive real eigenvalues (left) or a repeated positive real eigenvalue without two linearly independent eigenvectors (right).


Improper Nodal Sink: Distinct negative real eigenvalues (left) or a repeated negative real eigenvalue without two linearly independent eigenvectors (right).
Gallery of Typical Phase Portraits for the System x′=Ax: Saddles, Centers, Spirals, and Parallel Lines
FIGURE 7.4.16.
(Continued)

Saddle Point: Real eigenvalues of opposite sign.

Center: Pure imaginary eigenvalues.

Spiral Source: Complex conjugate eigenvalues with positive real part.

Spiral Sink: Complex conjugate eigenvalues with negative real part.

Parallel Lines: One zero and one negative real eigenvalue. (If the nonzero eigenvalue is positive, then the trajectories flow away from the dotted line.)

Parallel Lines: A repeated zero eigenvalue without two linearly independent eigenvectors.
7.4 Problems
For each of the systems in Problems 1 through 16 in Section 7.3, categorize the eigenvalues and eigenvectors of the coefficient matrix A according to Fig. 7.4.16 and sketch the phase portrait of the system by hand. Then use a computer system or graphing calculator to check your answer.
The phase portraits in Problems 17 through 28 correspond to linear systems of the form x′=Ax in which the matrix A has two linearly independent eigenvectors. Determine the nature of the eigenvalues and eigenvectors of each system. For example, you may discern that the system has pure imaginary eigenvalues, or that it has real eigenvalues of opposite sign; that an eigenvector associated with the positive eigenvalue is roughly [2−1]T, etc.


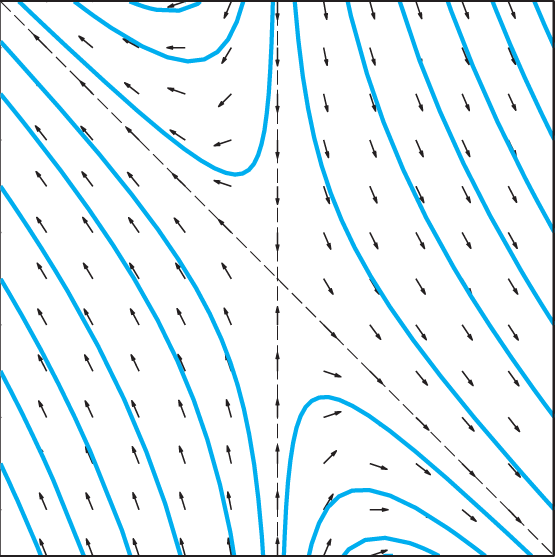









We can give a simpler description of the general solution
x(t)=c1[−16]e−2t+c2[11]e5t(9)of the system
x′=[416−1]xin Example 1 by introducing the oblique uv-coordinate system indicated in Fig. 7.4.17, in which the u- and v-axes are determined by the eigenvectors v1=[−16] and v2=[11], respectively.

FIGURE 7.4.17.
The oblique uv-coordinate system determined by the eigenvectors v1 and v2.
The uv-coordinate functions u(t) and v(t) of the moving point x(t) are simply its distances from the origin measured in the directions parallel to v1 and v2. It follows from (9) that a trajectory of the system is described by
u(t)=u0e−2t,v(t)=v0e5t(63)where u0=u(0) and v0=v(0). (a) Show that if v0=0, then this trajectory lies on the u-axis, whereas if u0=0, then it lies on the v-axis. (b) Show that if u0 and v0 are both nonzero, then a “Cartesian” equation of the parametric curve in Eq. (63) is given by v=Cu−5/2.
Use the chain rule for vector-valued functions to verify the principle of time reversal.
In Problems 31–33 A represents a 2×2 matrix.
Use the definitions of eigenvalue and eigenvector (Section 7.3) to prove that if λ is an eigenvalue of A with associated eigenvector v, then −λ is an eigenvalue of the matrix −A with associated eigenvector v. Conclude that if A has positive eigenvalues 0<λ2<λ1 with associated eigenvectors v1 and v2, then −A has negative eigenvalues −λ1<−λ2<0 with the same associated eigenvectors.
Show that the system x′=Ax has constant solutions other than x(t)≡0 if and only if there exists a (constant) vector x≠0 with Ax=0. (It is shown in linear algebra that such a vector x exists exactly when det(A)=0.)
(a) Show that if A has the repeated eigenvalue λ with two linearly independent associated eigenvectors, then every nonzero vector v is an eigenvector of A. (Hint: Express v as a linear combination of the linearly independent eigenvectors and multiply both sides by A.) (b) Conclude that A must be given by Eq. (22). (Suggestion: In the equation Av=λv take v=[10]Tand v=[01]T.)
Problems 35–37 show that all nontrivial solution curves of the system in Example 11 are ellipses rotated by the same angle as the trajectory in Fig. 7.4.11.
The system in Example 11 can be rewritten in scalar form as
x′1=6x1−17x2,x′2=8x1−6x2,leading to the first-order differential equation
dx2dx1=dx2/dtdx1/dt=8x1−6x26x1−17x2,or, in differential form,
(6x2−8x1)dx1+(6x1−17x2)dx2=0.Verify that this equation is exact with general solution
−4x21+6x1x2−172x22=k,(64)where k is a constant.
In analytic geometry it is shown that the general quadratic equation
Ax21+Bx1x2+Cx22=k(65)represents an ellipse centered at the origin if and only if Ak>0 and the discriminant B2−4AC<0. Show that Eq. (64) satisfies these conditions if k<0, and thus conclude that all nondegenerate solution curves of the system in Example 11 are elliptical.
It can be further shown that Eq. (65) represents in general a conic section rotated by the angle θ given by
tan 2θ=BA−C.Show that this formula applied to Eq. (64) leads to the angle θ=arctan24 found in Example 11, and thus conclude that all elliptical solution curves of the system in Example 11 are rotated by the same angle θ. (Suggestion: You may find useful the double-angle formula for the tangent function.)
Let v=[3+5i4]T be the complex eigenvector found in Example 11 and let z be a complex number. (a) Show that the real and imaginary parts ~a and ~b, respectively, of the vector ~v=z·v are perpendicular if and only if z=r(1±i) for some nonzero real number r. (b) Show that if this is the case, then ~a and ~b are parallel to the axes of the elliptical trajectory found in Example 11 (as Fig. 7.4.12 indicates).
Let A denote the 2×2 matrix
A=[abcd].Show that the characteristic equation of A (Eq. (3), Section 6.1) is given by
λ2−(a+d)λ+(ad−bc)=0.Suppose that the eigenvalues of A are pure imaginary. Show that the trace T(A)=a+d of A must be zero and that the determinant D(A)=ad−bc must be positive. Conclude that c≠0.
7.4 Application Dynamic Phase Plane Graphics
Using computer systems we can “bring to life” the static gallery of phase portraits in Fig. 7.4.16 by allowing initial conditions, eigenvalues, and even eigenvectors to vary in “real time.” Such dynamic phase plane graphics afford additional insight into the relationship between the algebraic properties of the 2×2 matrix A and the phase plane portrait of the system x′=Ax.
For example, the basic linear system
has general solution
where (a, b) is the initial point. If a≠0, then we can write
where c=b/ak. A version of the Maple commands
with(plots):
createPlot := proc(k)
soln := plot([exp(-t), exp(-k*t),
t = -10..10], x = -5..5, y = -5..5):
return display(soln):
end proc:
Explore(createPlot(k),
parameters = [k = -2.0..2.0])
produces Fig. 7.4.18, which allows the user to vary the parameter k continuously from k=−2 to k=2, thus showing dynamically the changes in the solution curves (1) in response to changes in k.

FIGURE 7.4.18.
Interactive display of the solution curves in Eq. (1). Using the slider, the value of k can be varied continuously from −2 to 2.
Figure 7.4.19 shows snapshots of the interactive display in Fig. 7.4.18 corresponding to the values −1,12, and 2 for the parameter k. Based on this progression, how would you expect the solution curves in Eq. (1) to look when k=1? Does Eq. (1) corroborate your guess?



FIGURE 7.4.19.
Snapshots of the interactive display in Fig. 7.4.18 with the initial conditions held fixed and the parameter k equal to −1,12, and 2, respectively.
As another example, a version of the Mathematica commands
a = {{-5, 17}, {-8, 7}};
x[t_] := {x1[t], x2[t]};
Manipulate[
soln = DSolve[{x′[t] == a.x[t],
x[0] == pt[[1]]}, x[t], t];
ParametricPlot[x[t]/.soln, {t, -3.5, 10},
PlotRange -> 5],
{{pt, {{4, 2}}}, Locator}]
was used to generate Fig. 7.4.20, which (like Figs. 7.4.13 and 7.4.14) shows the solution curve of the initial value problem
from Example 13 of the preceding section. However, in Fig. 7.4.20 the initial condition (4, 2) is attached to a “locator point” which can be freely dragged to any desired position in the phase plane, with the corresponding solution curve being instantly redrawn—thus illustrating dynamically the effect of varying the initial conditions.

FIGURE 7.4.20.
Interactive display of the initial value problem in Eq. (2). As the “locator point” is dragged to different positions, the solution curve is immediately redrawn, showing the effect of changing the initial conditions.

FIGURE 7.4.21.
Interactive display of the initial value problem x′=Ax with A given by Eq. (3). Both the initial conditions and the value of the parameter k can be varied dynamically.
Finally, Fig. 7.4.21 shows a more sophisticated, yet perhaps more revealing, demonstration. As you can verify, the matrix
has the variable eigenvalues 1 and k but with fixed associated eigenvectors [31]T and [1−3]T, respectively. Figure 7.4.21, which was generated by a version of the Mathematica commands
a[k ] := (1/10){{k + 9, 3 - 3k}, {3 - 3k, 9k + 1}}
x[t ] := {x1[t], x2[t]}
Manipulate[
soln[k ] = DSolve[{x′[t] == a[k].x[t],
x[0] == #}, x[t], t]&/@pt;
curve = ParametricPlot
[Evaluate[x[t]/.soln[k]], {t, -10, 10},
PlotRange -> 4], {k, -1, 1},
{{pt, {{2, -1}, {1, 2}, {-1, -2}, {-2, 1}}},
Locator}]
shows the phase portrait of the system x′=Ax with A given by Eq. (3). Not only are the initial conditions of the individual trajectories controlled independently by the “locator points,” but using the slider we can also vary the value of k continuously from −1 to 1, with the solution curves being instantly redrawn. Thus for a fixed value of k we can experiment with changing initial conditions throughout the phase plane, or, conversely, we can hold the initial conditions fixed and observe the effect of changing the value of k.
As a further example of what such a display can reveal, Fig. 7.4.22 consists of a series of snapshots of Fig. 7.4.21 where the initial conditions are held fixed and k progresses through the specific values −1, −0.25, 0, 0.5, 0.65, and 1. The result is a “video” showing stages in a transition from a saddle point with “hyperbolic” trajectories, to a pair of parallel lines, to an improper nodal source with “parabolic” trajectories, and finally to the exploding star pattern of a proper nodal source with straight-line trajectories. Perhaps these frames provide a new interpretation of the description “dynamical system” for a collection of interdependent differential equations.






FIGURE 7.4.22.
Snapshots of the interactive display in Fig. 7.4.21 with the initial conditions held fixed and the parameter k increasing from −1 to 1.
