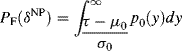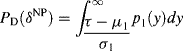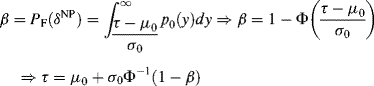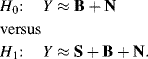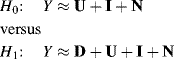3.5 Real Data-Based ROC Analysis

In real applications only a limited number of samples are available for data analysis, referred to as the power of the test. In this case, the data sample pool is generally not sufficiently large to constitute reliable statistics that can be used to characterize the LRT Λ(r) implemented by a detector. Under such a circumstance there is no effective means of producing Λ(r) and the ROC analysis must be carried out with data samples rather than statistics, p₀(r) and p₁(r).

3.5.1 How to Generate ROC Curves from Real Data

In what follows, we define

N = total number of data samples used for a particular detection method (technique)

N_signal = total number of data samples with presence of a signal (according to ground truth)

N_no-signal = total number of data samples with absence of a signal (according to ground truth)

N_D = total number of data samples with presence of a signal which is actually detected by the method

N_F = total number of data samples with absence of a signal, but claimed to have an signal detected by the method

N_M = total number of data samples with presence of a signal which is not detected by the method

N_TN = total number of data samples with presence of a signal and also claimed to have no signal detected by the method.

False alarm or false positive rate/probability is defined by

(3.10)

False negative or miss rate/probability:

(3.11)

Detection power/true-positive rate/probability:

(3.12)

True-negative rate/probability:

(3.13)

Based on (3.10)–(3.13), the following relationships are true:

(3.14)

(3.15)

with

(3.16)

3.5.2 How to Generate Gaussian-Fitted ROC Curves

Until now Equations (3.10)–(3.13), (3.14)–(3.16) are defined based on real samples. So, for a given set of sample pool used for testing any detection technique, only one point (P_D, P_F) can be generated for the ROC curve of a particular technique. Therefore, in order to produce a complete ROC curve for any specific detection technique (method), an infinite number of samples pool are required, which is practically impossible. One way to mitigate this difficulty is to assume that the noise in the binary hypothesis decision problem described by (3.1) is a zero-mean Gaussian distribution and the given sample pool is sufficiently large to generate reliable statistics. In this case, we can calculate the sample mean and variance for each hypothesis, and then assume these calculated sample means and variances to be the Gaussian means and variances under each hypothesis. With these new Gaussian distributions, finding the ROC curve of a specific detection technique (method) becomes feasible and can be actually derived mathematically from a standard signal detection theory as follows.

Now if we further assume that the probability density functions p₀(y) and p₁(y) in (3.1) that govern H₀ and H₁ are Gaussian distributions with means μ₀ and μ₁ and variances and calculated from a large pool of samples, respectively, the Λ(r) in (3.5) becomes . As a result, (3.6) and (3.7) can be further simplified to

(3.17)

(3.18)

where and are two Gaussian distributions with means μ₀ and μ₁ and variances and , respectively. Furthermore, if both of the variances and are set to 1, (3.25) and (3.26) simplify to most familiar forms:

(3.19)

(3.20)

Using Figure 3.3 as an example, a decision can be made by adjusting threshold τ via (3.19) and (3.20) where the regions corresponding to P_D, P_F, P_M, and P_TN are indicated with different shaded areas. For example, P_D is the area to the right of the threshold τ under the Gaussian distribution p₁(y) when H₁ is true and P_F is the area to the right of the threshold τ under the Gaussian distribution p₀(y) when H₀ is true. On the contrary, P_M is the area to the left of the threshold τ under the Gaussian distribution p₁(y) when H₁ is true and P_TN is the area to the left of the threshold τ under the Gaussian distribution p₀(y) when H₀ is true. It should be noted that the threshold τ is determined by the false alarm rate. If the false alarm rate is upper bounded by β in (3.4) with Gaussian distributions, using (3.17) we can calculate the corresponding τ by the following:

(3.21)

where Φ(x) is a standard Gaussian distribution given by

(3.22)

Therefore, the best decision to find an optimal threshold τ for (3.18) is (3.21) which is determined only by β. We now substitute τ given by (3.21) for τ in (3.18) and obtain the best detection power given by

(3.23)

Using (3.21) and (3.23) we can plot a Gaussian-fitted ROC curve of P_D versus P_F = β for real data.

3.5.3 How to Generate 3D ROC Curves

A major disadvantage resulting from the use of the traditional ROC curve is that both the detector statistics, Λ(r), implemented by the Neyman–Pearson detector δ^NP(r) and the threshold τ are independent parameters and are not specified in the ROC curve of (P_D, P_F) where P_D and P_F are actually dependent on Λ(r) and τ. Since the value of Λ(r) obtained from a data sample r is generally real valued and represents the detected signal strength present in r, that is, concentration level of a signal in r, a soft decision must be made directly on Λ(r) by varying the threshold τ instead of using the parameter β imposed on P_F. In doing so, we introduce a normalized detected signal strength of Λ(r) as

(3.24)

Using τ as a detection threshold value between 0 and 1 for (3.24) we can further define a normalized Neyman–Pearson detector, denoted by based on as follows:

(3.25)

which uses τ as a threshold value to convert the normalized real value of to a binary value. Accordingly, a “1” produced by (3.25) indicates that a target is detected; otherwise, there is no target present. By varying in (3.25), a family of detectors are generated for target detection, where for each τ the detector produces its pair of detection rate and a false alarm rate, (P_D, P_F). Therefore, if a third dimension is created to specify the threshold τ that is used to define a detector via (3.35), a 3D ROC curve can be generated and plotted based on three parameters, P_D, P_F and τ. With such a 3D ROC curve, three 2D ROC curves can also be generated, the 2D ROC curve of (P_D, P_F) which is the traditional ROC curve in Figure 3.1, a 2D ROC curve of (P_D,τ) and a 2D ROC curve of (P_F,τ). To generate a 3D ROC curve for real data, three steps are performed:

1. The data samples will be first classified into two categories, falsely alarmed sample pool Ω_FA and correctly detected sample pool Ω_D. The samples in Ω_FA are those samples which are detected as signal samples but actually contain no signals according to the ground truth. The detected sample pool Ω_D are those samples that are correctly detected by the normalized NP detector according to the ground truth. The sample set Ω_signal denotes the set of samples which actually have signal strength/concentration present in the r according to the ground truth.

2. Let Ω denote the total sample pool used for evaluation and Ω_S be the set of samples with signal presence, that is, samples with correctly detected and falsely missed signal samples (see (3.14)), and Ω_NS be the set of samples with signal absence, that is, samples with no signal detected and falsely detected signal samples (see (3.15)). In addition, let Ω_SD be the set of samples with detected signal strength/concentration greater than zero and Ω_NSD be the set of samples with no signal detected, that is, signal with zero strength/concentration. Then with and . The threshold τ in (3.21) is used to generate probabilities of falsely alarmed sample pool Ω_FA and signal detected sample pool Ω_SD.

3. For each threshold τ calculated in step 2, a pair of probabilities P_F and P_D are defined as follows, where N(A) denotes the number of samples in a sample pool A:

(3.26)

(3.27)

(3.28)

where , , and with , , and . (See the definitions given in Section 3.5.1 and = number of samples in X.)

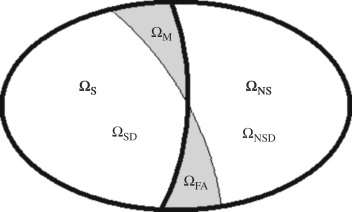
Figure 3.6 shows a diagram of relationships among Ω_S, Ω_SD, Ω_M, Ω_FA, Ω_NS, and Ω_NSD.

Figure 3.6 A diagram of relationships among Ω_S, Ω_SD, Ω_M, Ω_F, Ω_NS, and Ω_NSD.

In analogy with Section 3.5.2, we can also generate Gaussian fitted 3D ROC curves by the following steps:

1. Calculate sample means and variances for Ω_S and Ω_NS, denoted by μ_S, , and μ_NS, , respectively.

2. Find the Gaussian probability distributions under hypotheses H₀ and H₁, that is, for H₀ and for H₁.

3. Calculate the pair of probabilities P_F and P_D according to the following formulas:

(3.29)

(3.30)

It should be noted that the means and variances in (3.29) and (3.30) can be calculated from a given sample pool. For example, using the notations, N_no-signal and N defined in Section 3.5.1, we can calculate the μ₀, μ₁, and for (3.29) and (3.30) as follows:

(3.31)

(3.32)

(3.33)

(3.34)

where f(y_i) is the value of the ith sample y_i.

3.5.4 How to Generate 3D ROC Curves for Multiple Signal Detection and Classification

The hypothesis testing problem (3.1) considered so far assumes the standard signal detection in noise (SN) model where hypotheses H₀ and H₁ represent noise and signal + noise, respectively. There have been studies on extending (3.1) to two scenarios. One is called the signal/background/noise model proposed in Thai and Healey (2002) which includes background B as a third signal source described by

(3.35)

A second scenario is called the signal-decomposed interference/noise (SDIN) model suggested in Du and Chang (2004b) and is given by

(3.36)

where the signal source S considered in the SBN model (3.35) is further decomposed into the desired signal source D and the undesired signal source U and the background B considered in the SBN model is included in the interference signal source matrix I.

Using the SDIN model specified by (3.36), we can interpret various commonly used models as follows. When and D = S, the SDIN model is reduced to the standard SN model. If D = S and I = B with , then the SDIN model becomes the SBN model. The SDIN allows us to deal with multisignal detection and classification by interpret and signal sources as a signal source matrix comprising multiple signal sources with D = d representing the target signal source of interest to be detected and U being other target signal sources with no interest to d.

In order to extend a single target signal detection-based ROC analysis to a multiple-signal detection model specified by (3.36), we assume that there are p signal sources of interest, . Then the detection rate R_D(m_j) and false alarm rate R_F(m_j) for the jth signal source m_j defined by

(3.37)

(3.38)

where N_D(m_j) is the total number of true pixels which are m_j and detected as m_j, N_F(m_j) is the total number of true pixels which are not m_j but detected as m_j, N(m_j) is the total number of pixels that are specified by target signature m_j and N is the total number of pixels in the image. For detection of multiple signal sources, the detection rate/power P_D and false alarm rate P_F are then replaced by the mean detection rate and mean false alarm rate , respectively, which can be defined by taking the mean of R_D(m_j) and the mean of R_F(m_j) over all the p as

(3.39)

(3.40)

where , N(m_j) is the total number of pixels, which are, m_j and is the total number of all target pixels given by .

It notes that through specified by (3.25) along with (3.39) and (3.40) each of multiple signals, will be detected and classified jointly by a fixed and same threshold τ for all the p signal sources to produce a point in a 2D space given by . This is different from the single signal detection of m_j which uses its own and separate individual threshold τ_i in (3.25) to produce its own pair (P_D, P_F). However, such a subtle and crucial difference cannot be seen from the traditional 2D ROC curve of (P_D, P_F) since the threshold τ is hidden in P_D and P_F and the curve cannot show its influence on both P_D and P_F.

By decreasing τ from 1 to 0 in a third dimension, it results in a 3D mean-ROC curve, which can be used to evaluate the performance of a detector where the (x,y) coordinate is specified by (,τ) and the z-axis is specified by . Using this 3D mean-ROC curve we can further plot three 2D curves, a curve of versus which is the traditional ROC curve, a curve of versus τ and a curve of versus τ for detection performance analysis. Once the 2D ROC curve of (,) is generated, the area under the curve is calculated and defined as detection rate, which can be used to evaluate the effectiveness of a detector. The higher the detection rate the better the detector.