In probability theory, Bayes' theorem describes the probability of an event based on a prior knowledge of conditions that is related to that certain event. This is a theorem of probability originally stated by the Reverend Thomas Bayes. In other words, it can be seen as a way of understanding how the probability theory is true and affected by a new piece of information. For example, if cancer is related to age, the information about age can be used to assess the probability that a person might have cancer more accurately.

Bayes' theorem is stated mathematically as the following equation:

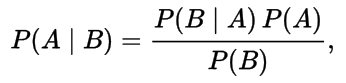
In the preceding equation, A and B are events with P (B) ≠ 0, and the other terms can be described as follows:

• P(A) and P(B) are the probabilities of observing A and B without regard to each other (that is, independence)
• P(A | B) is the conditional probability of observing event A given that B is true
• P(B| A) is the conditional probability of observing event B given that A is true

As you probably know, a well-known Harvard study shows that only 10% of happy people are rich. However, you might think that this statistic is very compelling but you might be somewhat interested in knowing the percentage of rich people are also really happy. Bayes' theorem helps you out on how to calculate this reserving statistic using two additional clues:

1. The percentage of people overall who are happy, that is, P(A).
2. The percentage of people overall who are rich, that is P(B).

The key idea behind Bayes' theorem is reversing the statistic considering the overall rates. Suppose that the following pieces of information are available as a prior:

1. 40% of people are happy and => P(A).
2. 5% of people are rich => P(B).

Now let's consider that the Harvard study is correct, that is, P(B|A) = 10%. Now the fraction of rich people who are happy, that is, P(A | B), can be calculated as follows:

P(A|B) = {P(A)* P(B| A)}/ P(B) = (40%*10%)/5% = 80%

Consequently, a majority of the people are also happy! Nice. To make it clearer, now let's assume the population of the whole world is 1,000 for simplicity. Then, according to our calculation, there are two facts that exist:

• Fact 1: This tells us 400 people are happy, and the Harvard study tells us that 40 of these happy people are also rich.
• Fact 2: There are 50 rich people altogether, and so the fraction who are happy is 40/50 = 80%.