40
MULTIVARIATE ANALYSIS IN API DEVELOPMENT
James C. Marek
Process Research and Development, AbbVie Inc., North Chicago, IL, USA
40.1 INTRODUCTION
When more than one variable is involved to determine a response, the mathematical space under consideration is multivariate. Chemical and biological processes are inherently multivariate, ensuring that the synthetic pharmaceutical and biopharmaceutical processes that rely on them are also multivariate in nature. Multivariate analysis (MVA) speaks specifically to the techniques within the statistical sciences that involve two or more variables. This chapter serves several purposes. As an introduction to MVA, it will give the reader a behind‐the‐scene understanding of the complex mathematical treatments. It is also intended to give the reader sufficient breadth and depth of the subject to convey the potential to benefit the process development effort and even support manufacturing controls.
Why is MVA important? MVA is recognized in ICH Q11 [1] as an important and integral part of the enhanced approach to process development. Specifically, the approach entails multivariate design of experiments, simulations, and modeling to establish control strategies for appropriate material specifications and process parameter ranges. Further, the US FDA provided guidance on process analytical technology (PAT) as early as 2004 [2]. PAT involves in situ measurements during operation of batch, semi‐batch, or continuous processes. PAT collects data in real time, affording several benefits such as (i) speedy acquisition of the desired information; (ii) the need for in‐process control samples in the manufacturing environment that may be replaced by PAT; (iii) process development data that may be collected essentially continuously throughout the duration of the experiment, without the need of human intervention or automatic samplers; (iv) the ability to track a process where traditional sampling is complicated by safety or sample stability considerations; and (v) acquisition of data to control the process in a feedback or feedforward control loop.
PAT may range from simple sensors to complex spectrometers. Thus, PAT includes providing simple measurements of parameters like density, conductivity, optical refractive index, single wavelength UV absorbance, etc. to very complex spectral data from infrared (IR) spectrometers, near‐IR spectrometers, Raman spectrometers, and laser diffraction analyzers. Analysis of data from simple sensors may be univariate; however the analysis of spectral data will rely on chemometrics. Chemometrics is defined as the statistical analysis of chemical data, and more often than not relies on multivariate statistical methods to incorporate the absorbance from more than one wavelength, Raman shift, particle chord length, etc. Spectra may be collected at frequent time intervals throughout the course of the process or experiment, allowing determination of reaction kinetics with multiple PAT instruments [3]. Each spectrum may contain hundreds, perhaps even thousands, of data points, consisting of the measured absorbances over a range of several hundred wave numbers.
40.2 APPROACHES TO MODEL DEVELOPMENT
The goal of quantitative MVA is often to develop a predictive model of the concentration of species of interest. This can be accomplished by either principal component regression (PCR) or the more commonly used technique of partial least squares (PLS). These techniques reduce the dimensionality of the data sets and involve factor spaces and eigenvectors, approaches that some researchers may find as somewhat complex and abstract. Therefore, it is useful to first consider some simpler, more traditional approaches for model development to assist understanding the more complex techniques.
40.2.1 Absorption Theory: Beer–Lambert Law
The absorption from a single species i at wavelength λ, Aλ, is proportional to the product of the absorption coefficient at the wavelength λ, αλ; the path length, L; and the species concentration, Ci:
In theory the concentration of species i could be determined by collecting spectra and using a single wavelength for the calibration. Assuming that compound i absorbs at multiple wavelengths, these absorptions could be combined to develop a multiple regression fitting of Ci with n wavelengths:
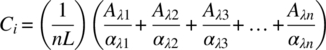
Combining terms for the constants to generate coefficients b1, b2, b3, …, bn,
Then a multiple regression equation for Ci results:
Figure 40.1 shows data from laboratory experiments for disappearance of a starting material (SM) (reactant) in a batch reactor from grab samples taken as a function of reaction time. The FTIR absorption noted for the SM was clear of overlap from other species in the system at a wavelength of 1397.32 cm−1. Hence, simple linear regression of the first derivatives at 1397.32 cm−1 was tested as an option to build a calibration model for the residual SM. The model, built using 72 data points collected in four experiments, yielded unsatisfactory predictions for the residual SM using spectra collected in a fifth experiment (Figure 40.1, hollow squares). Next, a multiple regression model was created to enable fitting the residual SM concentration (as determined by off‐line HPLC analysis of grab samples, PA%) to the mid‐IR absorbances collected in four of the experiments. The model was built using absorbances at four wave numbers and included three statistically significant two‐factor interactions. The model was then applied to the absorbance data from the fifth batch (hollow squares) to predict the SM concentration profile and compared to the corresponding HPLC data (Figure 40.2).
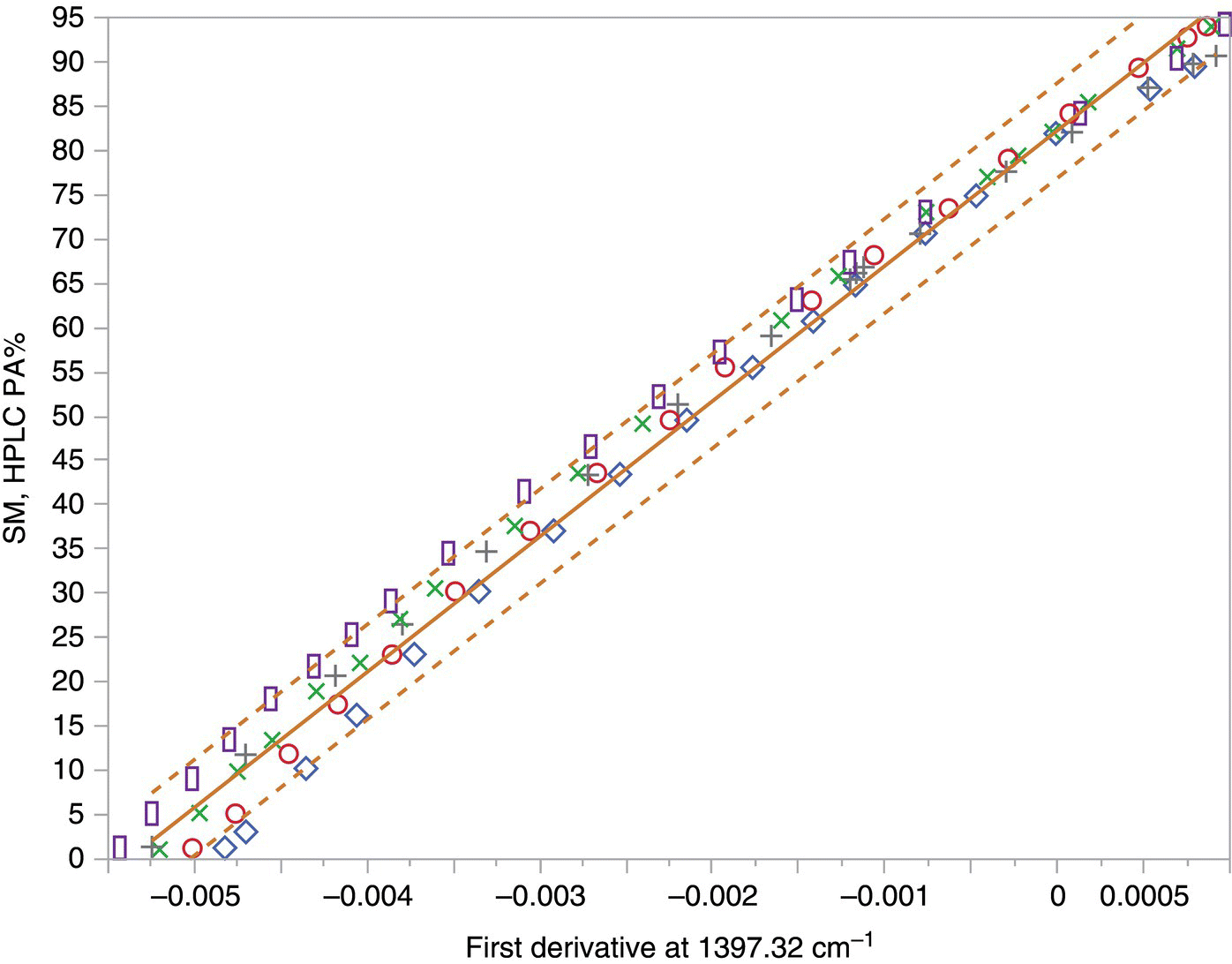
FIGURE 40.1 Residual SM from a reaction measured by HPLC PA% is plotted versus first derivative of mid‐IR absorption at 1397.32 cm−1. The five different symbols represent data from five separate laboratory reactions, the solid line is the regression fit, and the dashed line the 95% confidence interval for predicting an individual value.

FIGURE 40.2 Residual SM from a reaction measured by HPLC versus prediction from multiple regression fitted model for mid‐IR data. The five different symbols represent data from five separate laboratory reactions, the solid line is the regression fit, and the dashed line the 95% confidence interval.
The data suggest that the fit of the model to the calibration data from the four trials was excellent, but the model was not capable of accurately predicting the behavior of the fifth batch, particularly in the lower PA% region, which is the region of main interest to determine reaction completion in manufacturing batches. These examples from a complex reaction system illustrate cases where simple calibration models are unsatisfactory. Calibrations using a single wavelength, or multiple regression of absorbances from a few wavelengths, can be appropriate in some cases. For example, simple models may be suitable for analysis of solutions of high purity drug prepared for solubility determination.
In most systems of interest in pharmaceutical development, other species (reactants, solvents, related‐substance impurities, etc.) may be present that absorb at the same wavelength as the molecule of interest. Hence, we need to consider the contributions from more than one component to the observed absorption, in addition to more than one wavelength:
where
- An is the absorbance at the nth wavelength.
- αni is the absorbance coefficient at the nth wavelength for the ith component.
- L is the path length.
- Ci is the concentration of the ith component.
- i is the number of components.
This framework now has the absorbance at a given wavelength properly determined by the sum of the absorbances at that wavelength for each of the i components. The equation may be expressed in a modified form, taking b as the product of the absorption coefficient and the path length, wherein it becomes

This expression further simplifies to the matrix equation:
Here A is a single‐column absorbance matrix with n rows, (n × 1). B is a matrix of constants with n rows and i columns, and C is a single‐column concentration matrix with i rows, (i × 1). Hence, A(n × 1) = B(n × i) × C(i × 1). The B matrix is essentially a matrix of the absorbances produced at the n wavelengths with each of the i components at unit concentration.
It is a simple matter to extend the situation to the collection of spectra from more than one sample, each spectrum being generated from the unique concentrations of C1, C2, C3, …, Ci in the sample.
Let Ans be the absorbance at the nth wavelength for sample s, bni be the absorbance coefficient for at the nth wavelength times the path length for the ith component, and Cis be the concentration of the ith component in the sth sample, where there are n total components or chemical species. Now again we have the matrix equation, but now the A matrix will have a column for each spectrum, and the C matrix will have a column of concentration values for each sample. The matrix equation above holds, but now A is a s column absorbance matrix with n rows, C is s column concentration matrix with i rows, and B is a matrix of constants with n rows and i columns. Hence, in the matrix equation, A(n × s) = B(n × i) × C(i × s).
This forms the basis for calibration of spectroscopic data by the method of classical least squares (CLS). CLS involves the application of multiple linear regression to the Beer–Lambert equation of spectroscopy. A serious drawback of this approach is that the mathematics involved requires there be as many samples as there are wavelengths used in the calibration, and there may be hundreds of wavelengths being measured. To overcome this drawback, chemometricians rely on factor spaces and factor‐based techniques, chiefly principal component analysis (PCA), PCR, and PLS.
40.2.2 Principal Component Analysis
PCA is an orthogonal mathematical transformation to convert a set of observations that may be correlated into a smaller set of linearly uncorrelated variables termed the principal components, which are eigenvectors. In doing so, the dimensionality of the data set is reduced. For example, an IR spectrum with absorbance values measured at several hundred wave numbers may be reduced to considerably fewer, perhaps a handful of, principal components after PCA. PCA itself does not perform a regression; rather it operates on a set of data. Hence, p variables will end up with a set of p principal components [4].
The first principal component, PC1, is selected by finding a vector describing the maximum variation in the data set. To find the second principal component, PC2, a vector orthogonal to the first is identified that explains the greatest amount of the remaining variation in the data set. Additional principal components are found in this manner until the variation in the data set is explained to within the expected variation due to random error or noise. The determination of the appropriate numbers of principal components to include can be done by a variety of numerical methods. This is essential to avoid overfitting the data and creating inaccurate predictions by including too many factors that describe random error and noise. PCA by itself does not directly yield quantitative values for prediction of concentrations in samples, but is extremely useful to compare data collected under different processing conditions, such as monitoring reactions or crystallizations performed at different temperatures, reagent concentrations, etc.
To help visualize how principal components work, consider a two‐component system, a mixture of A and B. A solution of component A is prepared at exactly unit concentration (C = 1). Data are collected using a hypothetical spectrometer for which the spectra are assumed to be error‐free, and the absorbances measured at three wavelengths, λ1, λ2, and λ3. Similarly, a solution of component B is prepared at exactly unit concentration, and the absorbances are measured at the same three wavelengths, λ1, λ2, and λ3. The results are as shown in Table 40.1. A solution with no A or B is analyzed, and it shows zero absorbance at the three wavelengths. Next, additional solutions of A and B at various concentrations, including mixtures, are prepared. From Beer's law, for a solution of A prepared at twice the unit concentration, the absorbances will exactly double. Similarly, the absorbances from a mixture of A and B can be calculated by summing the product of their concentrations and the unit absorbances at each wavelength. The results for a series of these hypothetical noise and error‐free measurements on these samples are also shown in Table 40.1.
TABLE 40.1 Absorbances from Error‐Free Measurements of A and B
| Conc. of A | Conc. of B | |||
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0.5 | 0.25 |
| 2 | 0 | 2 | 1 | 0.5 |
| 3 | 0 | 3 | 1.5 | 0.75 |
| 0 | 1 | 0.25 | 0.5 | 1 |
| 0 | 2 | 0.5 | 1 | 2 |
| 0 | 3 | 0.75 | 1.5 | 3 |
| 1 | 1 | 1.25 | 1 | 1.25 |
| 1 | 2 | 1.5 | 1.5 | 2.25 |
| 1 | 3 | 1.75 | 2 | 3.25 |
| 1 | 4 | 2 | 2.5 | 4.25 |
| 1 | 5 | 2.25 | 3 | 5.25 |
| 1 | 6 | 2.5 | 3.5 | 6.25 |
| 1 | 7 | 2.75 | 4 | 7.25 |
| 2 | 1 | 2.25 | 1.5 | 1.5 |
| 2 | 2 | 2.5 | 2 | 2.5 |
| 2 | 3 | 2.75 | 2.5 | 3.5 |
| 2 | 4 | 3 | 3 | 4.5 |
| 2 | 5 | 3.25 | 3.5 | 5.5 |
| 2 | 6 | 3.5 | 4 | 6.5 |
| 2 | 7 | 3.75 | 4.5 | 7.5 |
| 3 | 1 | 3.25 | 2 | 1.75 |
| 3 | 2 | 3.5 | 2.5 | 2.75 |
| 3 | 3 | 3.75 | 3 | 3.75 |
| 3 | 4 | 4 | 3.5 | 4.75 |
| 3 | 5 | 4.25 | 4 | 5.75 |
| 3 | 6 | 4.5 | 4.5 | 6.75 |
| 3 | 7 | 4.75 | 5 | 7.75 |
| 4 | 1 | 4.25 | 2.5 | 2 |
| 4 | 2 | 4.5 | 3 | 3 |
| 4 | 3 | 4.75 | 3.5 | 4 |
| 4 | 4 | 5 | 4 | 5 |
| 4 | 5 | 5.25 | 4.5 | 6 |
| 4 | 6 | 5.5 | 5 | 7 |
| 4 | 7 | 5.75 | 5.5 | 8 |
| 5 | 1 | 5.25 | 3 | 2.25 |
| 5 | 2 | 5.5 | 3.5 | 3.25 |
| 5 | 3 | 5.75 | 4 | 4.25 |
| 5 | 4 | 6 | 4.5 | 5.25 |
| 5 | 5 | 6.25 | 5 | 6.25 |
| 5 | 6 | 6.5 | 5.5 | 7.25 |
| 5 | 7 | 6.75 | 6 | 8.25 |
| 6 | 1 | 6.25 | 3.5 | 2.5 |
| 6 | 2 | 6.5 | 4 | 3.5 |
| 6 | 3 | 6.75 | 4.5 | 4.5 |
| 6 | 4 | 7 | 5 | 5.5 |
| 6 | 5 | 7.25 | 5.5 | 6.5 |
| 6 | 6 | 7.5 | 6 | 7.5 |
| 6 | 7 | 7.75 | 6.5 | 8.5 |
Next, we can visualize the spectra in three‐dimensional space by plotting the absorbance of the first wavelength along one axis, the absorbance of the second wavelength along a second axis, and the absorbance of the third wavelength along the third axis. Figure 40.3 shows the plot for the data in Table 40.1.
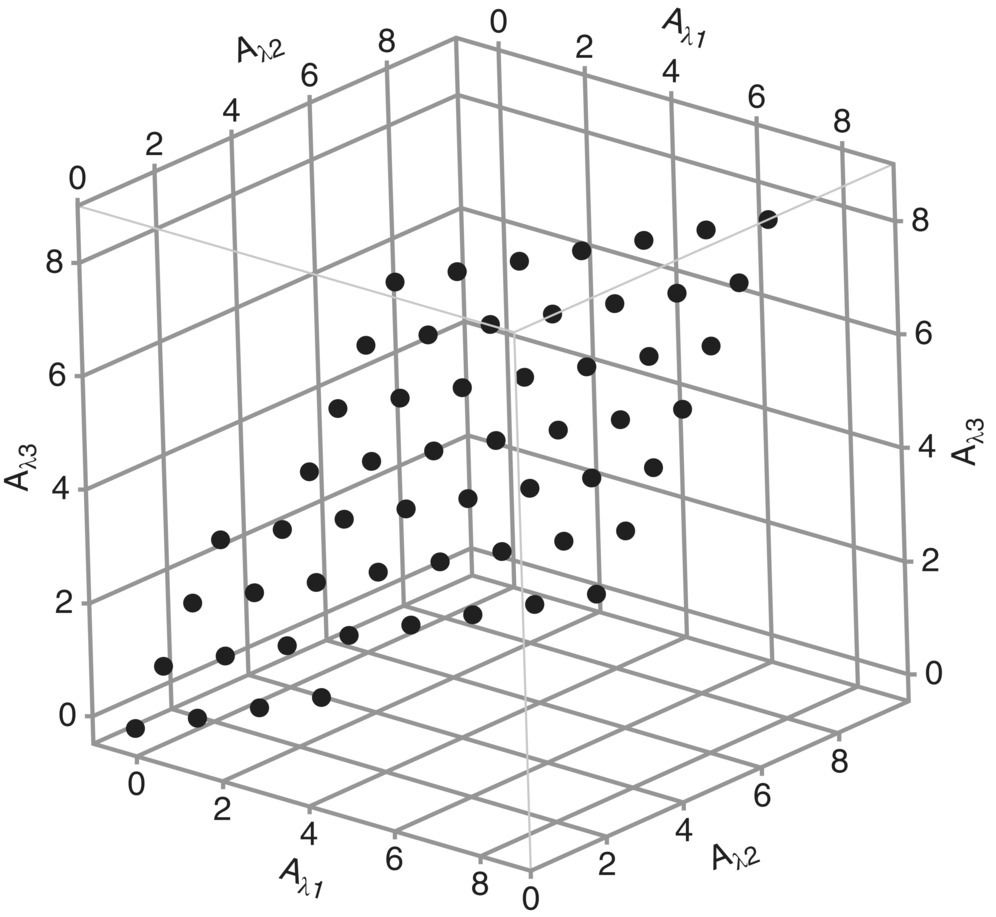
FIGURE 40.3 Absorption data from A and B mixtures from Table 40.1.
Note that the spectra, although measured at three wavelengths, lie in a two‐dimensional plane. Regardless of how many wavelengths are used in the measurements, even cases where several hundred wavelengths are used, the data for two components will lie in a two‐dimensional plane. The principal components are then found by finding the eigenvector in the direction of maximum variation of the data set and then a second eigenvector orthogonal to the first in a direction that accounts for the most of the remaining variation in the data set. The first principal component must lie in the plane of the data points to span the maximum possible variation of the data. Similarly, the second principal component will be orthogonal to the first but also lies in the plane of the data set. The principal components for this system are also shown in Figure 40.4. Note that the first principal component explains greater than 87% of the variation in the data set and the second explains a little less than 13%.
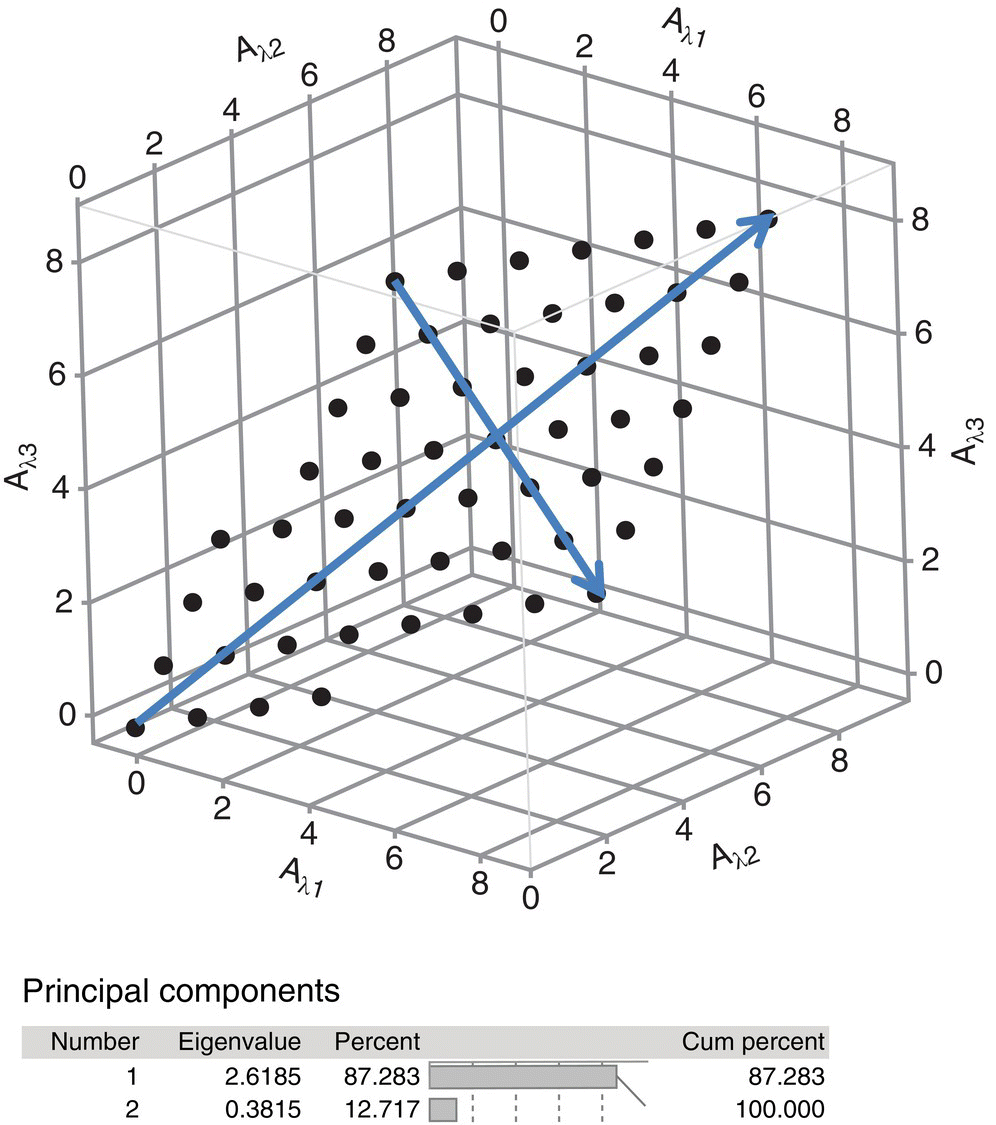
FIGURE 40.4 Principal components for A and B absorptions at  ,
, 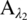 , and
, and 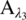 .
.
It is apparent that we could define a pair of axes in this plane that form a new coordinate system to plot the data and then describe each spectrum on the basis of the distance from the two new axes. This would reduce the dimensionality from 3 to 2. Similarly, had we used three chemical species, A, B, and C, and made similar measurements, the PCA would reduce the dimensionality to a data set described by three new axes.
For each of the data points, the distance of the data point from the PC1 or PC2 vector, often described as the projection of the data point onto the PC1 or PC2 vector, is called a score value. Scores are computed for each data point with respect to PC1 and then again for each data point with respect to a different principal component, typically PC2. Thus a score plot is created, PC1 versus PC2, which allows visualization of how different samples are related to one another. The eigenvalue of the eigenvector is the sum of squares of the projections of the data onto the eigenvector, and the projections are of course the distance along the vector of each data point. Principal component plots, termed loading plots, allow identification of how different variables are related to each other. Working with scaled variables is preferred, since the PCs and scores then become dimensionless variables.
Most commercial software packages output the eigenvalues of the principal component, as well as the relative amount of the variation in the data that is explained by each principal component, enabling interpretation as to the number of vectors needed to reduce the dimensionality of the data set.
40.2.3 Principal Component Regression (PCR)
For spectra collected on a set of samples of known concentration, the principal components of both the absorbances, X, and the known concentrations, Yn, can be calculated. For the set of observations, the matrix of regression coefficients, B, is computed:
This is termed building a calibration model. As additional spectra on samples of unknown concentration are collected in the future, it is possible to estimate the concentration of the unknowns, Yu, from the calibration model and the measured absorbance, Xu:
40.2.4 Partial Least Squares
PLS is an extension of PCR where again both the X and Y data are considered. However, the PLS equation or calibration is based on decomposing both the X and Y data into a set of scores and loadings, similar to PCR, but with one significant difference: the scores for both the X and Y data are not selected based solely on the direction of maximum variation, but instead are selected in order to maximize the correlation between the scores for both the X and Y variables. The result is termed a set of latent vectors, or basis vectors, or sometimes simply factors. The selection of the appropriate number of factors is important to properly fit the model, and the software packages have built‐in capability to recommend the number of factors to keep based on the predicted residual error sum of squares (PRESS residuals). Most commercial software packages [5] come with the ability to do PCA, PCR, and PLS.
PLS decomposition of X and Y into scores and loadings [5, 6] is given as
T and U are the score matrices for X and Y and P and Q are the loading matrices. PLS does not calculate the scores independently, but rather it seeks optimal congruence of the u and t vectors by using the u vector as the starting point for calculating the t vectors. This self‐consistent approach allows for a set of scores and loadings that represent the variation in the Y data set. Therefore, the scores and loadings are much better than PCR scores [4, 5] and loadings for quantitative prediction; hence PLS regression is the preferred technique for building calibration models and unknown prediction. The algorithm proceeds by mean centering the data and then finding the first loading spectrum and first component scores. The prediction of a PLS method is summarized in the regression vector or coefficient, B. The predictions are related to the X sample data by equation (Y = BX).
40.2.5 Data Preprocessing
It is important to note that while chemometric techniques may be applied to raw absorbance values, this is not usually the case. Before performing the various multivariate calibration and prediction techniques, some form of data transformation or preprocessing, while not mandatory, is nearly always warranted. There can be bias in the estimates if the predictors and the response variables are significantly different in magnitude, resulting in unequal leverage. Hence, each variable may be scaled by its mean and standard deviation to place the predictors and responses on more equal footing. Scaling the data at each wavelength as well as scaling of the response data used to derive the calibration is common. In fact, mean centering and scaling is so commonplace that some investigators take it for granted and do not report that they performed it prior to the analysis.
Derivative processing is common with mid‐IR and NIR spectra. Taking the first derivative of the spectra corrects for baseline shift during the data acquisition. Taking the second derivative of the spectra corrects for baseline drift. There are several methods for calculation of the spectral derivatives, with the most common being the method of Savitzky–Golay [7]. Examples of the raw absorbance spectrum and the resulting first derivatives of the spectra are shown in Figures 40.5 and 40.6.

FIGURE 40.5 Series of mid‐IR spectra absorbances from 600 to 1797 cm−1. The raw data are not centered or scaled.
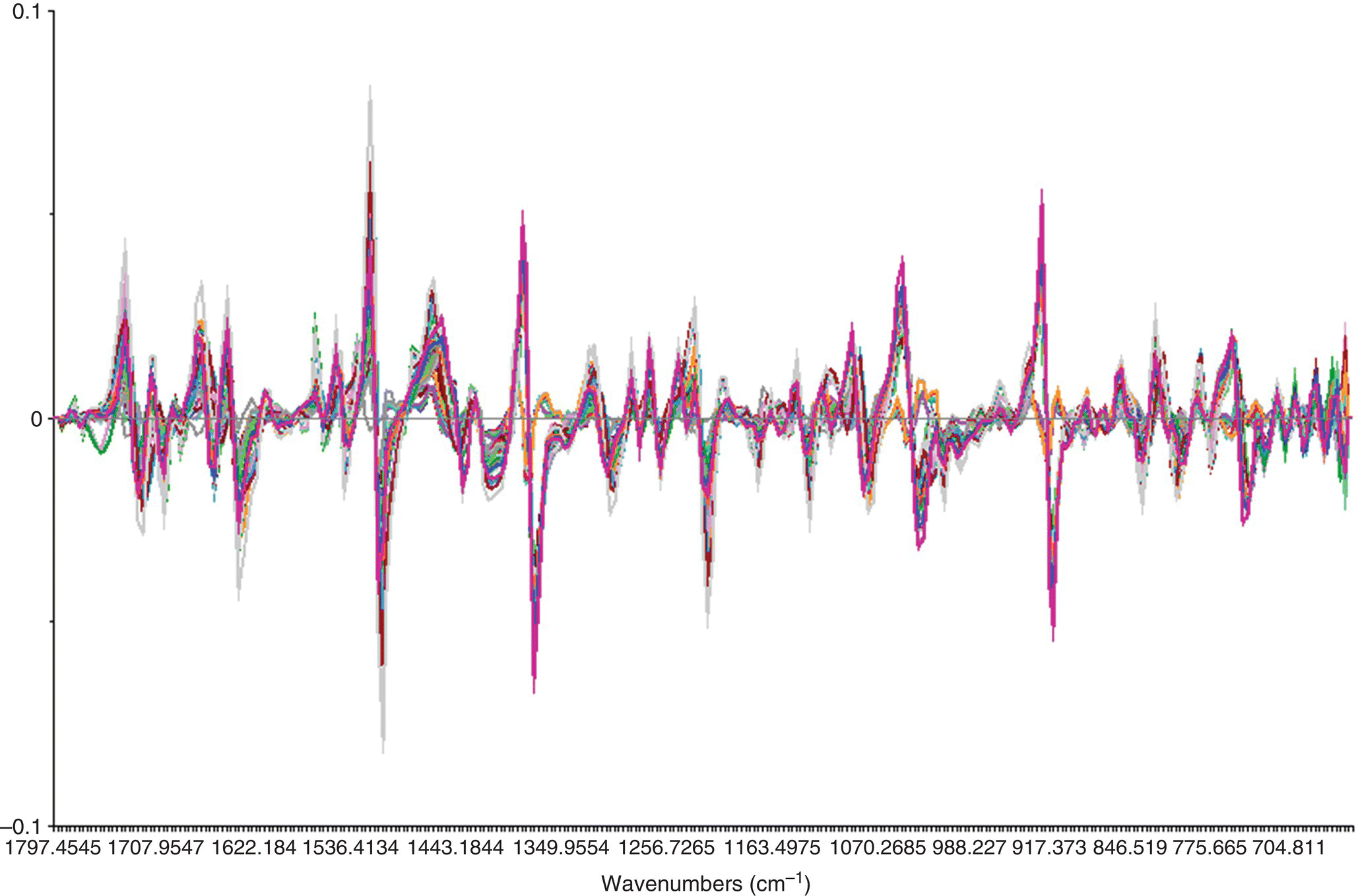
FIGURE 40.6 First derivative processing of mid‐IR spectra from Figure 40.4.
Depending on the sample type, particulate containing slurries and solutions may show light scattering effects with mid‐IR or NIR, and Raman spectra may exhibit background scattering. Hence, another technique applied to the spectra depending on the amount of diffuse reflectance is the multiplicative scattering correction (MSC). The pretreatments can be applied to the spectra or to the response data (y‐data).
40.3 BUILDING THE CALIBRATION MODEL
A more thorough discussion of methodologies in multivariate calibration model building is available in Ref. [8]. Building a chemometrics model would appear to be straightforward but can be deceptively tricky. A simple approach would be to prepare a set of samples containing the chemical species of interest dissolved in a relevant solvent at multiple, known concentrations, collect the spectra, and compute the calibration using PLS or PCR.
However, a calibration model built in this manner may prove deficient when applied to spectra collected from realistic chemical processing conditions, for example, monitoring the disappearance of a reactant, or the crystallization of an API from mother liquors. In both cases the spectral absorbances from the chemical species of interest may be mixed with absorbances from species in the system, such as reagents, solvents, impurities, and by‐products. Hence, although it requires more effort, it is usually more useful to build a robust calibration model by collecting spectra and simultaneously analyzing the solution for the concentration of desired analyte by an independent analytical method and perhaps also measuring the concentrations of the impurities in the sample.
Other factors to be considered when building the calibration model include whether there is temperature sensitivity of the spectral data and also the accuracy needed from the model. If the spectral data are temperature sensitive, it is possible to incorporate the temperature as a parameter in the model, with appropriate mean centering and scaling.
In many cases it is necessary to build a model over a limited range of concentrations to achieve the required accuracy or even to use multiple models to cover a broader concentration range.
40.4 CASE STUDY
A SM is converted to product by SN2 nucleophilic addition to a triflate intermediate. Formation of the triflate intermediate is accomplished by slow addition of trifluoromethanesulfonic anhydride (Tf2O), which reacts favorably at a hydroxyl site on the SM. The triflation is complicated by the presence of two other hydroxyl groups in the SM. Downstream purification relies on process chromatography. Undercharging Tf2O will leave residual SM, whereas overcharging Tf2O may lead to di‐ or tri‐triflates, since the SM has three hydroxyl groups. Large amounts of the residual SM or the multi‐triflated species challenge the downstream process chromatography; hence it is desired to charge as close to the exact amount of Tf2O for reaction completion as possible.
In situ ATR–FTIR was used to monitor the reaction at −35 and −50 °C in a pilot plant batch reactor. The SM and process solvent were charged to the reactor, and the internal temperature was adjusted to the desired value. A bolus of Tf2O was charged, and grab samples were taken for reaction completion by HPLC. Spectra were collected while the sample was analyzed, before the next bolus of Tf2O was charged. This created a steplike profile in the conversion of SM. Using principal component analysis, a score plot was generated. The score plot (Figure 40.7) shows a distinct difference between the −35 and −50 °C data, and subsequent investigation revealed differences in the purity of the reaction crudes. Ultimately, the reaction temperature set point was fixed at −50 °C, and all future batches were conducted at that temperature for better reaction purity profile. The data from the batch at −35 °C was not used in the subsequent chemometrics model development, in view of the difference in the score plot.

FIGURE 40.7 Score plot for triflation reaction at −35 and −50 °C.
Attempts to develop a predictive model for the residual SM concentration from the spectra using both simple and multiple linear regressions were described earlier in this chapter, with neither approach yielding a robust prediction. Using PLS regression, data from three pilot plant triflation batches at −50 °C were sufficient to develop a predictive model for residual SM levels. The regression used the spectral first derivatives and the appropriate HPLC analyses for residual SM, as measured by the relative peak area percentage remaining (PA%). A fourth pilot plant batch was performed, and the PLS model was applied to the spectral data to predict (off‐line) the residual SM levels. The predictions compared favorably to the HPLC PA% values (Figure 40.8) from grab samples taken during the reaction. An updated PLS model was then generated by including the data collected from all four batches at −50 °C. The refined PLS model was used to predict residual SM concentrations in real time in the fifth batch. The updated chemometrics model successfully predicted residual SM down to levels as low as 1 PA% (±1 PA%). Comparison of the model predictions to the off‐line HPLC PA% values taken during the reaction progress is shown in Figure 40.9. The results demonstrate the value of multivariate PLS analysis for obtaining accurate concentration measurements and for implementing advanced control strategies in complex chemical reaction systems.

FIGURE 40.8 Training set comparison for PLS model built with data from three batches using seven factors to predict the fourth batch off‐line. Also shown in the inset is the predicted residual error sum of squares (PRESS) as a function of number of factors.

FIGURE 40.9 Prediction of residual SM concentration via online PLS chemometrics model compared to HPLC analyses of grab samples taken during the reaction.
ACKNOWLEDGMENTS
This book chapter was sponsored by AbbVie. AbbVie contributed to the design, research, and interpretation of data, writing, reviewing, and approving of this chapter. James C. Marek is an employee of AbbVie.
REFERENCES
- 1. ICH (2012). International Conference on Harmonisation of Technical Requirements for Registration of Pharmaceuticals for Human Use, Development and Manufacture of Drug Substances (Chemical Entities and Biotechnological/Biological Entities) Q11, Step 4, 1 May 2012.
- 2. U.S. Food and Drug Administration (2004). Guidance for Industry Process Analytical Technology. Rockville, MD: U.S. Food and Drug Administration.
- 3. Ehly, M. and Gemperline, P.J. (2007). Analytica Chimica Acta 595: 80–88.
- 4. Kramer, R. (1998). Chemometric Techniques for Quantitative Analysis. Boca Raton, FL: CRC Press, Taylor & Francis.
- 5. Esbensen, K. (2002). Multivariate Data Analysis – In Practice. Oslo, Norway: CAMO Process AS.
- 6. Chiang, L.H., Russell, E.L., and Braatz, R.D. (2001). Fault Detection and Diagnosis. London: Springer.
- 7. Savitzky, A. and Golay, M.H.E. (1962). Analytical Chemistry 36: 1627–1639.
- 8. Martens, H. and Naes, T. (1989). Multivariate Calibration. Chicester: Wiley.
