10.1 Cluster Analysis
This section sets up the groundwork for studying cluster analysis. Section 10.1.1 defines cluster analysis and presents examples of where it is useful. In Section 10.1.2, you will learn aspects for comparing clustering methods, as well as requirements for clustering. An overview of basic clustering techniques is presented in Section 10.1.3.
10.1.1 What Is Cluster Analysis?
Cluster analysis or simply clustering is the process of partitioning a set of data objects (or observations) into subsets. Each subset is a cluster, such that objects in a cluster are similar to one another, yet dissimilar to objects in other clusters. The set of clusters resulting from a cluster analysis can be referred to as a clustering. In this context, different clustering methods may generate different clusterings on the same data set. The partitioning is not performed by humans, but by the clustering algorithm. Hence, clustering is useful in that it can lead to the discovery of previously unknown groups within the data.
Cluster analysis has been widely used in many applications such as business intelligence, image pattern recognition, Web search, biology, and security. In business intelligence, clustering can be used to organize a large number of customers into groups, where customers within a group share strong similar characteristics. This facilitates the development of business strategies for enhanced customer relationship management. Moreover, consider a consultant company with a large number of projects. To improve project management, clustering can be applied to partition projects into categories based on similarity so that project auditing and diagnosis (to improve project delivery and outcomes) can be conducted effectively.
In image recognition, clustering can be used to discover clusters or “subclasses” in handwritten character recognition systems. Suppose we have a data set of handwritten digits, where each digit is labeled as either 1, 2, 3, and so on. Note that there can be a large variance in the way in which people write the same digit. Take the number 2, for example. Some people may write it with a small circle at the left bottom part, while some others may not. We can use clustering to determine subclasses for “2,” each of which represents a variation on the way in which 2 can be written. Using multiple models based on the subclasses can improve overall recognition accuracy.
Clustering has also found many applications in Web search. For example, a keyword search may often return a very large number of hits (i.e., pages relevant to the search) due to the extremely large number of web pages. Clustering can be used to organize the search results into groups and present the results in a concise and easily accessible way. Moreover, clustering techniques have been developed to cluster documents into topics, which are commonly used in information retrieval practice.
As a data mining function, cluster analysis can be used as a standalone tool to gain insight into the distribution of data, to observe the characteristics of each cluster, and to focus on a particular set of clusters for further analysis. Alternatively, it may serve as a preprocessing step for other algorithms, such as characterization, attribute subset selection, and classification, which would then operate on the detected clusters and the selected attributes or features.
Because a cluster is a collection of data objects that are similar to one another within the cluster and dissimilar to objects in other clusters, a cluster of data objects can be treated as an implicit class. In this sense, clustering is sometimes called automatic classification. Again, a critical difference here is that clustering can automatically find the groupings. This is a distinct advantage of cluster analysis.
Clustering is also called data segmentation in some applications because clustering partitions large data sets into groups according to their similarity. Clustering can also be used for outlier detection, where outliers (values that are “far away” from any cluster) may be more interesting than common cases. Applications of outlier detection include the detection of credit card fraud and the monitoring of criminal activities in electronic commerce. For example, exceptional cases in credit card transactions, such as very expensive and infrequent purchases, may be of interest as possible fraudulent activities. Outlier detection is the subject of Chapter 12.
Data clustering is under vigorous development. Contributing areas of research include data mining, statistics, machine learning, spatial database technology, information retrieval, Web search, biology, marketing, and many other application areas. Owing to the huge amounts of data collected in databases, cluster analysis has recently become a highly active topic in data mining research.
As a branch of statistics, cluster analysis has been extensively studied, with the main focus on distance-based cluster analysis. Cluster analysis tools based on k-means, k-medoids, and several other methods also have been built into many statistical analysis software packages or systems, such as S-Plus, SPSS, and SAS. In machine learning, recall that classification is known as supervised learning because the class label information is given, that is, the learning algorithm is supervised in that it is told the class membership of each training tuple. Clustering is known as unsupervised learning because the class label information is not present. For this reason, clustering is a form of learning by observation, rather than learning by examples. In data mining, efforts have focused on finding methods for efficient and effective cluster analysis in large databases. Active themes of research focus on the scalability of clustering methods, the effectiveness of methods for clustering complex shapes (e.g., nonconvex) and types of data (e.g., text, graphs, and images), high-dimensional clustering techniques (e.g., clustering objects with thousands of features), and methods for clustering mixed numerical and nominal data in large databases.
10.1.2 Requirements for Cluster Analysis
Clustering is a challenging research field. In this section, you will learn about the requirements for clustering as a data mining tool, as well as aspects that can be used for comparing clustering methods.
The following are typical requirements of clustering in data mining.
■ Scalability: Many clustering algorithms work well on small data sets containing fewer than several hundred data objects; however, a large database may contain millions or even billions of objects, particularly in Web search scenarios. Clustering on only a sample of a given large data set may lead to biased results. Therefore, highly scalable clustering algorithms are needed.
■ Ability to deal with different types of attributes: Many algorithms are designed to cluster numeric (interval-based) data. However, applications may require clustering other data types, such as binary, nominal (categorical), and ordinal data, or mixtures of these data types. Recently, more and more applications need clustering techniques for complex data types such as graphs, sequences, images, and documents.
■ Discovery of clusters with arbitrary shape: Many clustering algorithms determine clusters based on Euclidean or Manhattan distance measures (Chapter 2). Algorithms based on such distance measures tend to find spherical clusters with similar size and density. However, a cluster could be of any shape. Consider sensors, for example, which are often deployed for environment surveillance. Cluster analysis on sensor readings can detect interesting phenomena. We may want to use clustering to find the frontier of a running forest fire, which is often not spherical. It is important to develop algorithms that can detect clusters of arbitrary shape.
■ Requirements for domain knowledge to determine input parameters: Many clustering algorithms require users to provide domain knowledge in the form of input parameters such as the desired number of clusters. Consequently, the clustering results may be sensitive to such parameters. Parameters are often hard to determine, especially for high-dimensionality data sets and where users have yet to grasp a deep understanding of their data. Requiring the specification of domain knowledge not only burdens users, but also makes the quality of clustering difficult to control.
■ Ability to deal with noisy data: Most real-world data sets contain outliers and/or missing, unknown, or erroneous data. Sensor readings, for example, are often noisy—some readings may be inaccurate due to the sensing mechanisms, and some readings may be erroneous due to interferences from surrounding transient objects. Clustering algorithms can be sensitive to such noise and may produce poor-quality clusters. Therefore, we need clustering methods that are robust to noise.
■ Incremental clustering and insensitivity to input order: In many applications, incremental updates (representing newer data) may arrive at any time. Some clustering algorithms cannot incorporate incremental updates into existing clustering structures and, instead, have to recompute a new clustering from scratch. Clustering algorithms may also be sensitive to the input data order. That is, given a set of data objects, clustering algorithms may return dramatically different clusterings depending on the order in which the objects are presented. Incremental clustering algorithms and algorithms that are insensitive to the input order are needed.
■ Capability of clustering high-dimensionality data: A data set can contain numerous dimensions or attributes. When clustering documents, for example, each keyword can be regarded as a dimension, and there are often thousands of keywords. Most clustering algorithms are good at handling low-dimensional data such as data sets involving only two or three dimensions. Finding clusters of data objects in a high-dimensional space is challenging, especially considering that such data can be very sparse and highly skewed.
■ Constraint-based clustering: Real-world applications may need to perform clustering under various kinds of constraints. Suppose that your job is to choose the locations for a given number of new automatic teller machines (ATMs) in a city. To decide upon this, you may cluster households while considering constraints such as the city’s rivers and highway networks and the types and number of customers per cluster. A challenging task is to find data groups with good clustering behavior that satisfy specified constraints.
■ Interpretability and usability: Users want clustering results to be interpretable, comprehensible, and usable. That is, clustering may need to be tied in with specific semantic interpretations and applications. It is important to study how an application goal may influence the selection of clustering features and clustering methods.
The following are orthogonal aspects with which clustering methods can be compared:
■ The partitioning criteria: In some methods, all the objects are partitioned so that no hierarchy exists among the clusters. That is, all the clusters are at the same level conceptually. Such a method is useful, for example, for partitioning customers into groups so that each group has its own manager. Alternatively, other methods partition data objects hierarchically, where clusters can be formed at different semantic levels. For example, in text mining, we may want to organize a corpus of documents into multiple general topics, such as “politics” and “sports,” each of which may have subtopics, For instance, “football,” “basketball,” “baseball,” and “hockey” can exist as subtopics of “sports.” The latter four subtopics are at a lower level in the hierarchy than “sports.”
■ Separation of clusters: Some methods partition data objects into mutually exclusive clusters. When clustering customers into groups so that each group is taken care of by one manager, each customer may belong to only one group. In some other situations, the clusters may not be exclusive, that is, a data object may belong to more than one cluster. For example, when clustering documents into topics, a document may be related to multiple topics. Thus, the topics as clusters may not be exclusive.
■ Similarity measure: Some methods determine the similarity between two objects by the distance between them. Such a distance can be defined on Euclidean space, a road network, a vector space, or any other space. In other methods, the similarity may be defined by connectivity based on density or contiguity, and may not rely on the absolute distance between two objects. Similarity measures play a fundamental role in the design of clustering methods. While distance-based methods can often take advantage of optimization techniques, density- and continuity-based methods can often find clusters of arbitrary shape.
■ Clustering space: Many clustering methods search for clusters within the entire given data space. These methods are useful for low-dimensionality data sets. With high-dimensional data, however, there can be many irrelevant attributes, which can make similarity measurements unreliable. Consequently, clusters found in the full space are often meaningless. It’s often better to instead search for clusters within different subspaces of the same data set. Subspace clustering discovers clusters and subspaces (often of low dimensionality) that manifest object similarity.
To conclude, clustering algorithms have several requirements. These factors include scalability and the ability to deal with different types of attributes, noisy data, incremental updates, clusters of arbitrary shape, and constraints. Interpretability and usability are also important. In addition, clustering methods can differ with respect to the partitioning level, whether or not clusters are mutually exclusive, the similarity measures used, and whether or not subspace clustering is performed.
10.1.3 Overview of Basic Clustering Methods
There are many clustering algorithms in the literature. It is difficult to provide a crisp categorization of clustering methods because these categories may overlap so that a method may have features from several categories. Nevertheless, it is useful to present a relatively organized picture of clustering methods. In general, the major fundamental clustering methods can be classified into the following categories, which are discussed in the rest of this chapter.
Partitioning methods: Given a set of n objects, a partitioning method constructs k partitions of the data, where each partition represents a cluster and k ≤ n. That is, it divides the data into k groups such that each group must contain at least one object. In other words, partitioning methods conduct one-level partitioning on data sets. The basic partitioning methods typically adopt exclusive cluster separation. That is, each object must belong to exactly one group. This requirement may be relaxed, for example, in fuzzy partitioning techniques. References to such techniques are given in the bibliographic notes (Section 10.9).
Most partitioning methods are distance-based. Given k, the number of partitions to construct, a partitioning method creates an initial partitioning. It then uses an iterative relocation technique that attempts to improve the partitioning by moving objects from one group to another. The general criterion of a good partitioning is that objects in the same cluster are “close” or related to each other, whereas objects in different clusters are “far apart” or very different. There are various kinds of other criteria for judging the quality of partitions. Traditional partitioning methods can be extended for subspace clustering, rather than searching the full data space. This is useful when there are many attributes and the data are sparse.
Achieving global optimality in partitioning-based clustering is often computationally prohibitive, potentially requiring an exhaustive enumeration of all the possible partitions. Instead, most applications adopt popular heuristic methods, such as greedy approaches like the k-means and the k-medoids algorithms, which progressively improve the clustering quality and approach a local optimum. These heuristic clustering methods work well for finding spherical-shaped clusters in small- to medium-size databases. To find clusters with complex shapes and for very large data sets, partitioning-based methods need to be extended. Partitioning-based clustering methods are studied in depth in Section 10.2.
Hierarchical methods: A hierarchical method creates a hierarchical decomposition of the given set of data objects. A hierarchical method can be classified as being either agglomerative or divisive, based on how the hierarchical decomposition is formed. The agglomerative approach, also called the bottom-up approach, starts with each object forming a separate group. It successively merges the objects or groups close to one another, until all the groups are merged into one (the topmost level of the hierarchy), or a termination condition holds. The divisive approach, also called the top-down approach, starts with all the objects in the same cluster. In each successive iteration, a cluster is split into smaller clusters, until eventually each object is in one cluster, or a termination condition holds.
Hierarchical clustering methods can be distance-based or density- and continuity-based. Various extensions of hierarchical methods consider clustering in subspaces as well.
Hierarchical methods suffer from the fact that once a step (merge or split) is done, it can never be undone. This rigidity is useful in that it leads to smaller computation costs by not having to worry about a combinatorial number of different choices. Such techniques cannot correct erroneous decisions; however, methods for improving the quality of hierarchical clustering have been proposed. Hierarchical clustering methods are studied in Section 10.3.
Density-based methods: Most partitioning methods cluster objects based on the distance between objects. Such methods can find only spherical-shaped clusters and encounter difficulty in discovering clusters of arbitrary shapes. Other clustering methods have been developed based on the notion of density. Their general idea is to continue growing a given cluster as long as the density (number of objects or data points) in the “neighborhood” exceeds some threshold. For example, for each data point within a given cluster, the neighborhood of a given radius has to contain at least a minimum number of points. Such a method can be used to filter out noise or outliers and discover clusters of arbitrary shape.
Density-based methods can divide a set of objects into multiple exclusive clusters, or a hierarchy of clusters. Typically, density-based methods consider exclusive clusters only, and do not consider fuzzy clusters. Moreover, density-based methods can be extended from full space to subspace clustering. Density-based clustering methods are studied in Section 10.4.
Grid-based methods: Grid-based methods quantize the object space into a finite number of cells that form a grid structure. All the clustering operations are performed on the grid structure (i.e., on the quantized space). The main advantage of this approach is its fast processing time, which is typically independent of the number of data objects and dependent only on the number of cells in each dimension in the quantized space.
Using grids is often an efficient approach to many spatial data mining problems, including clustering. Therefore, grid-based methods can be integrated with other clustering methods such as density-based methods and hierarchical methods. Grid-based clustering is studied in Section 10.5.
These methods are briefly summarized in Figure 10.1. Some clustering algorithms integrate the ideas of several clustering methods, so that it is sometimes difficult to classify a given algorithm as uniquely belonging to only one clustering method category. Furthermore, some applications may have clustering criteria that require the integration of several clustering techniques.
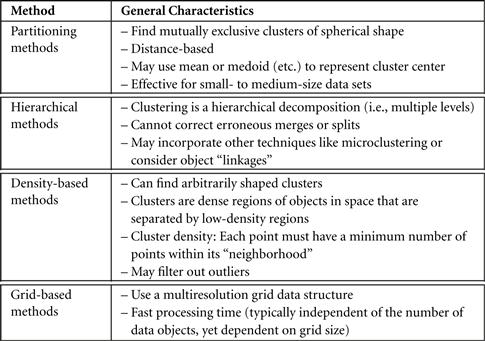
Figure 10.1 Overview of clustering methods discussed in this chapter. Note that some algorithms may combine various methods.
In the following sections, we examine each clustering method in detail. Advanced clustering methods and related issues are discussed in Chapter 11. In general, the notation used is as follows. Let D be a data set of n objects to be clustered. An object is described by d variables, where each variable is also called an attribute or a dimension, and therefore may also be referred to as a point in a d-dimensional object space. Objects are represented in bold italic font (e.g., p).
