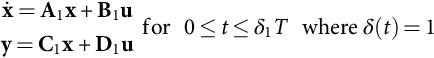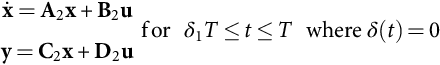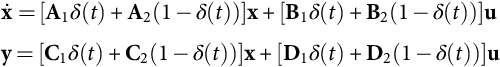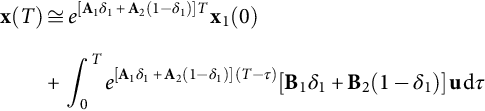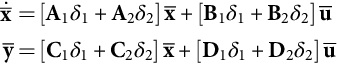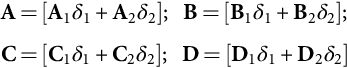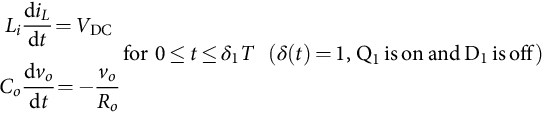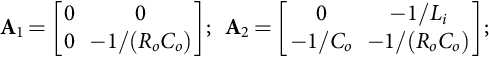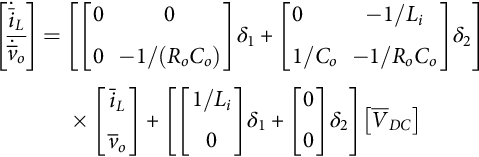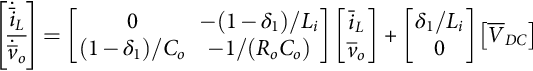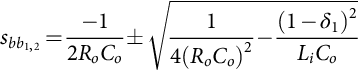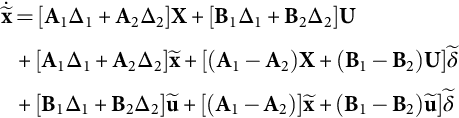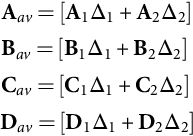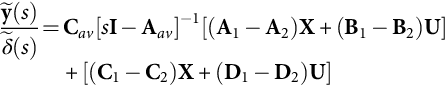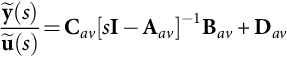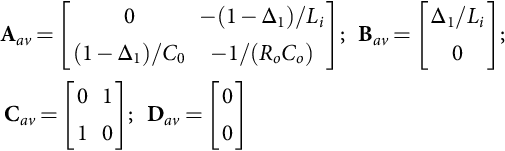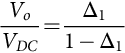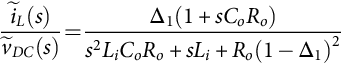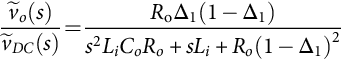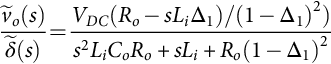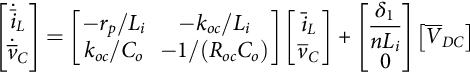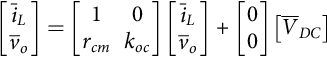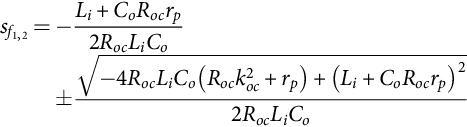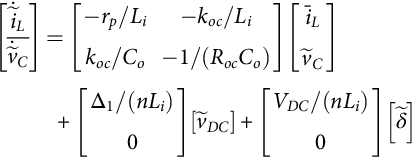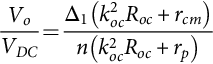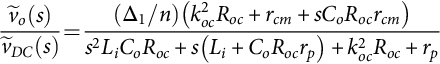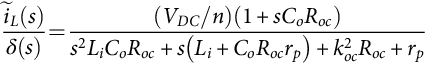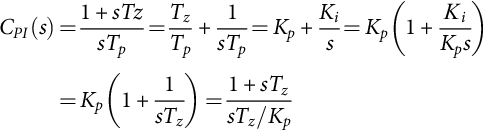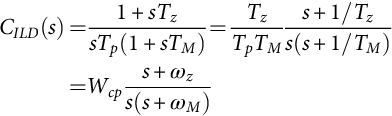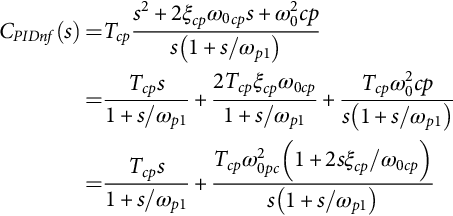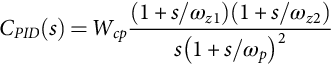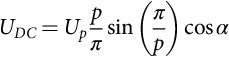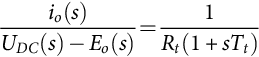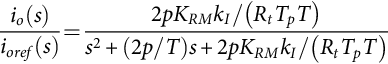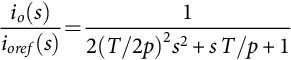Linear and Nonlinear Control of Switching Power Converters
José Fernando Silva Universidade de Lisboa, Lisboa, Portugal
Sónia F. Pinto Universidade de Lisboa, Lisboa, Portugal
Abstract
This chapter provides tools to control switching electronic power converters. It starts by explaining techniques to obtain linear state-space converter models, illustrating them through examples. Linear models are then used to design linear feedback controllers for converter operating in the continuous or discontinuous mode.
Nonlinear state-space models and sliding-mode controllers are next used to define exactly the variables to be measured while providing the control and switching laws aiming for robust modulator and controller design.
Predictive control uses a detailed nonlinear dynamic model to forecast the converter future behavior upon application of every possible converter switching state or vector. The best vector is then applied to the converter by computing the minimum of a cost functional.
Fuzzy control needs an expert qualitative knowledge of the converter dynamics. The steps to obtain a fuzzy controller are described, and the provided example compares the fuzzy controller performance to current-mode control.
The backstepping control methodology is explained using a recursive procedure interconnecting the selection of the candidate Lyapunov function with the design of the feedback control loop, to obtain stability and robust control under conditions less restrictive than other methods.
Keywords
State-space average modeling; Linear control; Sliding mode; Predictive control; Fast predictive control; Backstepping control
Acknowledgments
Authors thank all the researchers whose works contributed to this chapter, namely, professors V. Pires, D. Barros, J. Quadrado, T. Amaral, M. Crisóstomo, L. Encarnação, and Aranzazu D. Martin; engineers J. Costa and N. Rodrigues; and the suggestions of Professor M. P. Kazmierkowski. This work was supported by national funds through Fundação para a Ciência e a Tecnologia (FCT) with reference UID/CEC/50021/2013 and by POSI, POCTI, and FEDER past projects enabling the presented results.
35.1 Introduction
Switching power converters must be suitably designed and controlled in order to supply the voltages, currents, or frequency ranges needed for the load and to guarantee the requested dynamics [1–4]. Furthermore, they can be designed to serve as “clean” interfaces between most loads and the electric utility system. Thereafter, the set switching power converter plus load behaves as an almost pure electric utility resistive load.
This chapter provides basic and advanced skills to control electronic power converters, taking into account that the control of switching power converters is a vast and interdisciplinary subject. Control designers for switching power converters should know the static and dynamic behavior of the electronic power converter and how to design its elements for the intended operating modes. Designers must be experts on control techniques, especially the nonlinear ones, since switching converters are nonlinear, time-variant, discrete systems, and designers must be capable of analog or digital implementation of the derived modulators, regulators, or compensators. Powerful modeling methodologies and sophisticated control processes must be used to obtain stable-controlled switching power converters, not only with satisfactory static and dynamic performance but also with low sensitivity against load or line disturbances or, preferably, robustness.
In Section 35.2, the techniques to obtain suitable nonlinear and linear state-space models, for most switching converters, are presented and illustrated through examples. The derived linear models are used to create equivalent circuits and to design linear feedback controllers for converters operating in the continuous or discontinuous mode. The classical linear time-invariant system control theory, based on Laplace transform, transfer function concepts, Bode plots, or root locus, is best used with state-space averaged models or derived circuits and well-known triangular wave modulators for generating the switching variables or the trigger signals for the power semiconductors.
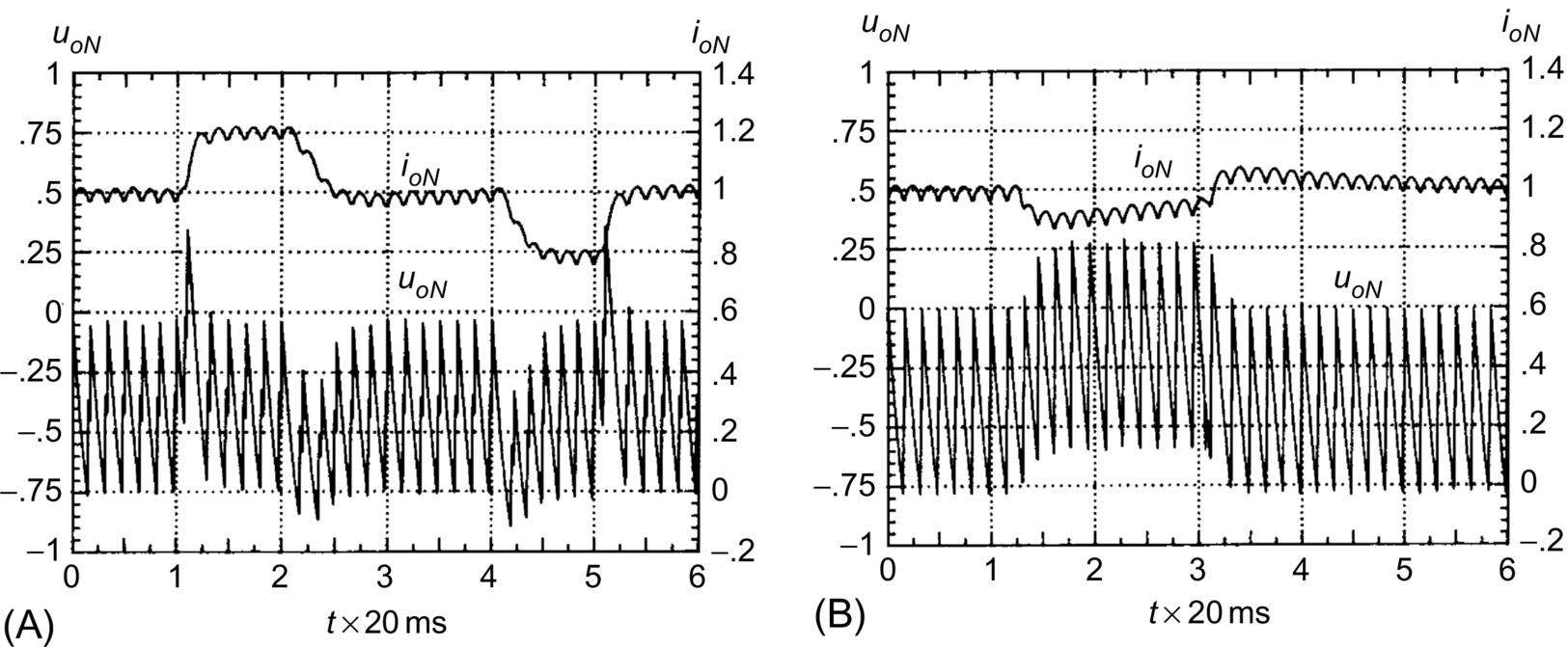
Nonlinear state-space models and sliding-mode controllers, presented in Section 35.3, provide a more consistent way of handling the control problem of switching converters, since sliding mode is aimed at variable structure systems, as are switching power converters. Chattering, a characteristic of sliding mode, is inherent to switching power converters, even if they are controlled with linear methods. Chattering is very hard to remove and is acceptable in certain converter variables. The described sliding-mode methodology defines exactly the variables that need to be measured, while providing the necessary equations (control law and switching law) whose implementation gives the robust modulator and compensator low-level hardware (or software). Therefore, the sliding-mode control integrates the design of the switching converter modulator and controller electronics, reducing the needed designer expertise. This approach requires measurement of the state variables but eliminates conventional modulators and linear feedback compensators, enabling better performance and robustness. It also reduces the converter cost, control complexity, volume, and weight (increasing power density). The so-called main drawback of sliding mode, variable switching frequency, is also addressed, providing fixed-frequency auxiliary functions and suitable augmented control laws to null steady-state errors due to the use of constant switching frequency.
Predictive control (Section 35.4) uses a detailed nonlinear dynamic model (including system bounds, saturations, and hysteresis) of the switching power converter to forecast the converter future behavior upon application of every possible switching state or vector. For all possible switching states (vectors), the control errors are evaluated and weighted, and the vector that leads to the minimum value of a suitable cost function is selected and applied to the converter. Predictive controllers also integrate the design of the switching converter modulator and controller electronics using fast microprocessors or fast algorithms. The steps in designing a predictive optimum controller for switching power converters with finite small number of switching states are explained in Section 35.4. Upon choosing a suitable cost function, obtained converter performances are usually better than obtained using linear or even sliding-mode controllers. This arises as sliding mode tries to go as fast as possible toward the sliding regime but chatters along the sliding surface, while predictive control aims to zero the error at the next sampling step.
In contrast, fuzzy control of switching converters (Section 35.5) is a control technique that needs no converter models, parameters, or operating conditions, but only an expert qualitative knowledge of the converter dynamics. Fuzzy controllers can be used in a diverse array of switching converters with only small adaptations, since the controllers, based on fuzzy sets, are obtained simply from the knowledge of the system dynamics, using a model reference adaptive control philosophy. Obtained fuzzy control rules can be built into a decision-lookup table, in which the control processor simply picks up the control input corresponding to the sampled measurements. Fuzzy controllers are almost resistant to system parameter fluctuations, since they do not take into account their values. The steps to obtain a fuzzy controller are described, and the example provided compares the fuzzy controller performance to the current-mode control.
Backstepping control (Section 35.6) is presented as a recursive method for stabilizing the origin of a converter modeled in a strict-feedback form. The procedure interconnects the choice of a candidate Lyapunov function with the design of the feedback control loop using Lyapunov's second method. Backstepping offers stability, tracking, and robust control under conditions less restrictive than other methods. Integral action is included to ensure the convergence, in steady state, of the tracking error to zero, regardless of nonmodeled disturbances and parameter uncertainty. Backstepping control is a nonlinear method that can be used with conventional fixed-frequency duty-cycle modulators for power converters to prevent chattering at variable frequency.
35.2 Switching Power Converter Control Using State-Space Averaged Models
35.2.1 Introduction
State-space models provide a general and strong basis for dynamic modeling of various systems including switching converters. State-space models are useful to design the needed linear control loops and can also be used to computer simulate the steady state and the dynamic behavior, of the switching converter, fitted with the designed feedback control loops and subjected to external perturbations. Furthermore, state-space models are the basis for applying powerful nonlinear control methods such as sliding mode. State-space averaging and linearization provide an elegant solution for the application of widely known linear control techniques to most switching power converters.
35.2.2 State-Space Modeling
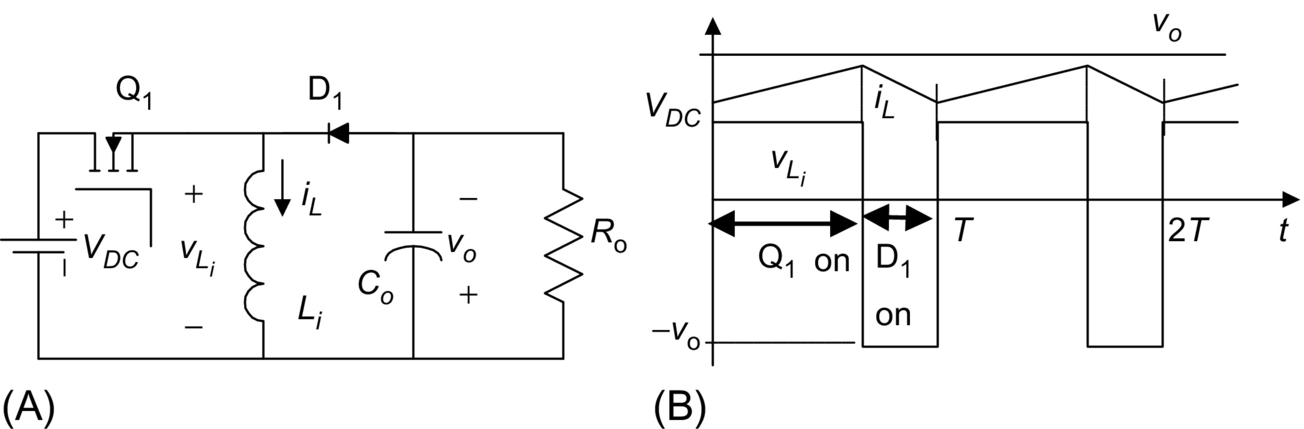
Consider a switching power converter with sets of power semiconductor structures, each one with two different circuit configurations, according to the state of the respective semiconductors, and operating in the continuous mode of conduction. Supposing the power semiconductors as controlled ideal switches (zero on-state voltage drops, zero off-state currents, and instantaneous commutation between the on- and off-states), the time (t) behavior of the circuit, over period T, can be represented by the general form of the state-space model Eq. (35.1):
˙x=Ax+Buy=Cx+Du
where x is the state vector; ˙x=dx/dt![]() ; u is the input or control vector; y is the output vector; and A, B, C, and D are, respectively, the dynamics (or state), the input, the output, and the direct transmission (or feedforward) matrices.
; u is the input or control vector; y is the output vector; and A, B, C, and D are, respectively, the dynamics (or state), the input, the output, and the direct transmission (or feedforward) matrices.
Since the power semiconductors will be either conducting or blocking, a time-dependent switching variable δ(t) can be used to describe the allowed switch states of each structure (i.e., δ(t)=1 for the on-state circuit and δ(t)=0 for the off-state circuit). Then, two subintervals must be considered: subinterval 1 for 0≤t≤δ1T, when δ(t)=1, where δ1 is the duty ratio between the on-state and the off-state, and subinterval 2 for δ1T≤t≤T when δ(t)=0. The state equations of the circuit, in each of the circuit configurations, can be written as
˙x=A1x+B1uy=C1x+D1ufor0≤t≤δ1Twhereδ(t)=1
˙x=A2x+B2uy=C2x+D2uforδ1T≤t≤Twhereδ(t)=0
35.2.2.1 Switched State-Space Model
Given the two binary values of the switching variable δ(t), Eqs. (35.2) and (35.3) can be combined to obtain the nonlinear and time-variant switched state-space model of the switching converter circuit, Eq. (35.4) or (35.5):
˙x=[A1δ(t)+A2(1−δ(t))]x+[B1δ(t)+B2(1−δ(t))]uy=[C1δ(t)+C2(1−δ(t))]x+[D1δ(t)+D2(1−δ(t))]u
˙x=ASx+BSuy=CSx+DSu
where AS=[A1δ(t)+A2(1−δ(t))], BS=[B1δ (t)+B2 (1−δ (t))], CS=[C1δ (t)+C2 (1−δ (t))], and DS=[D1δ (t)+D2 (1−δ (t))].
35.2.2.2 State-Space Averaged Model
Since the state variables of the x vector are continuous, using Eq. (35.4), with the initial conditions x1(0)=x2(T) and x2(δ1 T)=x1(δ1 T), and considering the duty cycle δ1 as the average value of δ(t), the time evolution of the converter state variables can be obtained, integrating Eq. (35.4) over the intervals 0≤t≤δ1 T and δ1 T≤t≤T, although it often requires excessive calculation effort. However, a convenient approximation can be devised, considering λmax, the maximum of the absolute values of all eigenvalues of A (usually, λmax is related to the cutoff frequency fc of an equivalent low-pass filter with fc≪1/T). For λmax T≪1, the exponential matrix (or state transition matrix) eAt=I+At+A2t 2/2+…+Ant n/n!, where I is the identity or unity matrix, can be approximated by eAt≈I+At. Therefore, eA1δ1 t·eA2(1−δ1)t≈I + [A1δ1+A2(1−δ1)]t. Hence, the solution over the period T, for the system represented by Eq. (35.4), is found to be
x(T)≅e[A1δ1+A2(1−δ1)]Tx1(0)+∫T0e[A1δ1+A2(1−δ1)](T−τ)[B1δ1+B2(1−δ1)]udτ
This approximate response of Eq. (35.4) is identical to the exact response obtained from the nonlinear continuous time-invariant state-space model (35.7), supposing that the average values of x, denoted ˉx![]() , are the new state variables and considering δ2=1−δ1. Moreover, if A1 A2=A2 A1, the approximation is exact:
, are the new state variables and considering δ2=1−δ1. Moreover, if A1 A2=A2 A1, the approximation is exact:
˙ˉx=[A1δ1+A2δ2]ˉx+[B1δ1+B2δ2]ˉuˉy=[C1δ1+C2δ2]ˉx+[D1δ1+D2δ2]ˉu
For λmaxT≪1, the model (35.7), often referred to as the state-space averaged model, is also said to be obtained by “averaging” Eq. (35.4) over one period, under small ripple and slow variations, as the average of products is approximated by products of the averages. Comparing Eq. (35.7) with Eq. (35.1), the relations (35.8), defining the state-space averaged model, are obtained:
A=[A1δ1+A2δ2];B=[B1δ1+B2δ2];C=[C1δ1+C2δ2];D=[D1δ1+D2δ2]
Since λmax is the maximum of the absolute values of all the eigenvalues of A, the model (35.14) and (35.15) is valid for switching frequencies fs (fs=1/T) that verify λmaxT≪1. Therefore, as T≪1/λmax, the values of T that approximately verify this restriction are T≪1/max(|sbb1,2|). Given these buck-boost converter data, T≪2 ms is obtained. Therefore, the converter switching frequency must obey fs≫max(|sbb1,2|), implying switching frequencies above, say, 5 kHz. Consequently, the buck-boost switching frequency, the inductor value, and the capacitor value were chosen accordingly.
This restriction can be further used to discuss the maximum frequency ωmax for which the state-space averaged model is still valid, given a certain switching frequency. As λmax can be regarded as a frequency, the preceding constraint brings ωmax≪2πfs, say ωmax<2πfs/10, which means that the state-space averaged model is a good approximation at frequencies under one-tenth of the power converter switching frequency.
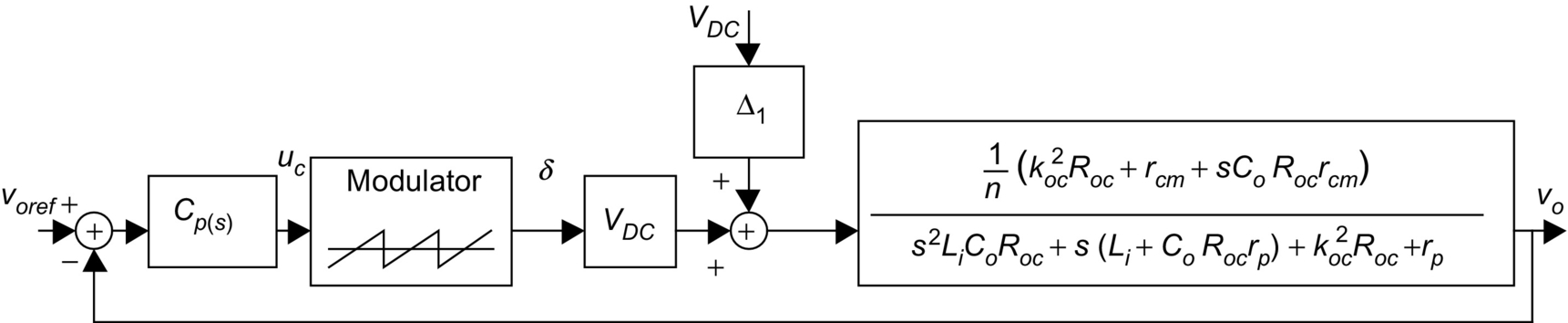
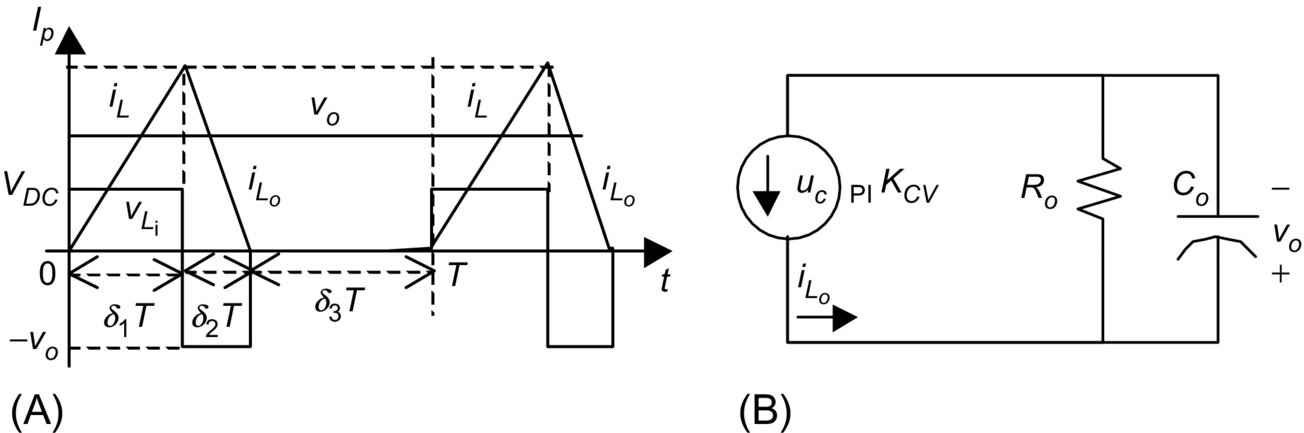
The state-space averaged model (35.14) and (35.15) is also the state-space model of the circuit represented in Fig. 35.2. Hence, this circuit is often named “the averaged equivalent circuit” of the buck-boost converter and allows the determination, under small ripple and slow variations, of the average equivalent circuit of the converter switching cell (power transistor plus diode).

The average equivalent circuit of the switching cell (Fig. 35.3A) is represented in Fig. 35.3B and emerges directly from the state-space averaged model (35.14) and (35.15). This equivalent circuit can be viewed as the model of an “ideal transformer” (Fig. 35.3C), whose primary to secondary ratio (v1/v2) can be calculated applying Kirchhoff's voltage law to obtain−v1+vs−v2=0. As v2=δ1vs, it follows that v1=vs(1−δ1), giving (v1/v2)=(1−δ1)/δ1. The same ratio could be obtained beginning with iL=i1+i2 and i1=δ1iL (Fig. 35.3B), which gives i2=iL(1−δ1) and (i2/i1)=δ2/δ1.

The average equivalent circuit concept, obtained from Eq. (35.7) or Eqs. (35.14) and (35.15), can be applied to other switching converters, with or without a similar switching cell, to obtain transfer functions or to simulate the converter average behavior. The average equivalent circuit of the switching cell can be applied to converters with the same switching cell operating in the continuous conduction mode. However, note that the state variables of Eq. (35.7) or Eqs. (35.14) and (35.15) are the mean values of the converter instantaneous variables and, therefore, do not represent their ripple components. The inputs of the state-space averaged model are the mean values of the converter inputs over one switching period.
35.2.2.3 Linearized State-Space Averaged Model
The converter outputs ˉy![]() must be regulated actuating on the duty cycle δ(t), and the converter inputs ū usually present perturbations due to the load and power supply variations. State variables are decomposed in small ac perturbations (denoted by “~”) and dc steady-state quantities (represented by uppercase letters). Therefore,
must be regulated actuating on the duty cycle δ(t), and the converter inputs ū usually present perturbations due to the load and power supply variations. State variables are decomposed in small ac perturbations (denoted by “~”) and dc steady-state quantities (represented by uppercase letters). Therefore,
ˉx=X+˜xˉy=Y+˜yˉu=U+˜uδ1=Δ1+˜δδ2=Δ2−˜δ
Using Eq. (35.17) in Eq. (35.7) and rearranging terms, it is obtained:
˙˜x=[A1Δ1+A2Δ2]X+[B1Δ1+B2Δ2]U+[A1Δ1+A2Δ2]˜x+[(A1−A2)X+(B1−B2)U]˜δ+[B1Δ1+B2Δ2]˜u+[(A1−A2)]˜x+(B1−B2)˜u]˜δ
Y+˜y=[C1Δ1+C2Δ2]X+[D1Δ1+D2Δ2]U+[C1Δ1+C2Δ2]˜x+[(C1−C2)X+(D1−D2)U]˜δ+[D1Δ1+D2Δ2]˜u+[(C1−C2)]˜x+(D1−D2)˜u]˜δ
The terms [A1Δ1+A2 Δ2] X + [B1 Δ1+B2 Δ2] U and [C1 Δ1+C2 Δ2] X + [D1 Δ1+D2 Δ2] U, respectively, from Eqs. (35.18) and (35.19) represent the steady-state behavior of the system. As in steady-state ˙X=0![]() , the following relationships hold:
, the following relationships hold:
0=[A1,Δ1,+,A2,Δ2]X+[B1,Δ1,+,B2,Δ2]U
Y=[C1,Δ1,+,C2,Δ2]X+[D1,Δ1,+,D2,Δ2]U
Neglecting higher-order terms ([(A1−A2)˜x+(B1−B2)˜u)]˜δ≈0![]() of Eqs. (35.18) and (35.19), the linearized small-signal state-space averaged model is
of Eqs. (35.18) and (35.19), the linearized small-signal state-space averaged model is
˙˜x=[A1Δ1+A2Δ2]˜x+[(A1−A2)X+(B1−B2)U]˜δ+[B1Δ1+B2Δ2]˜u˜y=[C1Δ1+C2Δ2]˜x+[(C1−C2)X+(D1−D2)U]˜δ+[D1Δ1+D2Δ2]˜u
or
˙˜x=Aav˜x+Bav˜u+[(A1−A2)X+(B1−B2)U]˜δ˜y=Cav˜x+Dav˜u+[(C1−C2)X+(D1−D2)U]˜δ
with
Aav=[A1Δ1+A2Δ2]Bav=[B1Δ1+B2Δ2]Cav=[C1Δ1+C2Δ2]Dav=[D1Δ1+D2Δ2]
35.2.3 Converter Transfer Functions
Using Eq. (35.20) in Eq. (35.21), the input U to output Y steady-state relations (35.25), needed for open-loop and feedforward control, can be obtained:
YU=−CavA−1avBav+Dav
Applying Laplace transforms to Eq. (35.23) with zero initial conditions and using the superposition theorem, the small-signal duty-cycle ˜δ![]() -to-output ỹ transfer functions (35.26) can be obtained considering zero line perturbations (ũ=0):
-to-output ỹ transfer functions (35.26) can be obtained considering zero line perturbations (ũ=0):
˜y(s)˜δ(s)=Cav[sI−Aav]−1[(A1−A2)X+(B1−B2)U]+[(C1−C2)X+(D1−D2)U]
The line-to-output transfer function (or audio susceptibility transfer function) (35.27) is derived using the same method, considering now zero small-signal duty-cycle perturbations (˜δ=0)![]() :
:
˜y(s)˜u(s)=Cav[sI−Aav]−1Bav+Dav
35.2.4 Pulse Width Modulator Transfer Functions
In what is often referred to as the pulse-width-modulation (PWM) voltage-mode control, the output voltage uc(t) of the error (between desired and actual output) amplifier plus regulator, processed if needed, is compared with a repetitive or carrier waveform r(t), to obtain the switching variable δ(t) (Fig. 35.6A). This function controls the power switch, turning it on at the beginning of the period and turning it off when the ramp exceeds the uc(t) voltage. In Fig. 35.6B, the opposite occurs (turnoff at the end of the period and turn-on when the uc(t) voltage exceeds the ramp).

Considering r(t) as represented in Fig. 35.6A (r(t)=ucmaxt/T), δk is obtained equating r(t)=uc giving δk=uc (t)/ucmax or δk/uc (t)=GM (GM =1/ucmax). In Fig. 35.6B, the switching-on angle αk is obtained from r(t)=ucmax−2ucmaxωt/π and uc (t)=ucmax−2ucmax αk/π, giving αk=(π/2)×(1−uc/ucmax) and GM=∂αk/∂uc=−π/(2ucmax).
Since, after turnoff or turn-on, any control action variation of uc(t) will only affect the converter duty cycle in the next period (or sample for digital hardware), a time delay is introduced in the control loop. For simplicity, with small-signal perturbations around the operating point, this delay is assumed almost constant and equal to its mean value (T/2). Then, the transfer function of the PWM modulator is
˜δ(s)˜uc(s)=GMe−sT/2=GMes(T/2)=GM1+sT2+s22!(T2)2+…+sjj!(T2)j+…≈GM1+sT2
The final approximation of Eq. (35.48), valid for ωT/2<√2/2![]() , [7] suggests that the PWM modulator can be considered as an amplifier with gain GM and a dominant pole. Notice that this pole occurs at a frequency doubling the switching frequency, and most state-space averaged models are valid only for frequencies below one-tenth of the switching frequency. Therefore, in most situations, this modulator pole can be neglected, being simply δ(s)=GMuc(s), as the dominant pole of Eq. (35.48) stays at least one decade to the left of the dominant poles of the converter.
, [7] suggests that the PWM modulator can be considered as an amplifier with gain GM and a dominant pole. Notice that this pole occurs at a frequency doubling the switching frequency, and most state-space averaged models are valid only for frequencies below one-tenth of the switching frequency. Therefore, in most situations, this modulator pole can be neglected, being simply δ(s)=GMuc(s), as the dominant pole of Eq. (35.48) stays at least one decade to the left of the dominant poles of the converter.
35.2.5 Linear Feedback Design Ensuring Stability
In the application of classical linear feedback control to switching power converters, Bode plots and root locus are, usually, suitable methods to assess system performance and stability. General rules for the design of the compensated open-loop transfer function are as follows:
The low-frequency gain should be high enough to minimize output steady-state errors.
The frequency of 0 dB gain (unity gain), ω0dB, should be placed close to the maximum allowed by the modeling approximations (λmaxT≪1), to allow fast response to transients. In practice, this frequency should be almost an order of magnitude lower than the switching frequency.
To ensure stability, the phase margin, defined as the additional phase shift needed to render the system unstable without gain changes (or the difference between the open-loop system phase at ω0dB and −180°), must be positive and in general greater than 30° (45−70° is desirable). In the root locus, no poles should enter the right half of the complex plane.
To increase stability, the gain should be less than −30 dB at the frequency where the phase reaches −180° (gain margin greater than 30 dB).
Transient behavior and stability margins are related: The obtained damping factor is generally 0.01 times the phase margin (in degrees), and overshoot (in percent) is given approximately by 75° minus the phase margin. The product of the rise time (in seconds) and the closed-loop bandwidth (in rad/s) is close to 2.8.
To guarantee gain and phase margins, the following series compensation transfer functions (usually implemented with operational amplifiers) are often used [8]:
35.2.5.1 Types of Compensation
Lag and lead compensation
Lag compensation should be used in converters with good stability margin but poor steady-state accuracy. If the frequencies 1/Tp and 1/Tz of Eq. (35.49) with 1/Tp<1/Tz are chosen sufficiently below the unity gain frequency, lag-lead compensation lowers the loop gain at high frequency but maintains the phase unchanged for frequencies f≫1/Tz. Then, the dc gain can be increased to reduce the steady-state error without significantly decreasing the phase margin:
CLL(s)=kLL1+sTz1+sTp=kLLTzTps+1/Tzs+1/Tp
Lead compensation can be used in converters with good steady-state accuracy but poor stability margin. If the frequencies 1/Tp and 1/Tz of Eq. (35.49) with 1/Tp>1/Tz are chosen below the unity gain frequency, lead-lag compensation increases the phase margin without significantly affecting the steady-state error. The Tp and Tz values are chosen to increase the phase margin, fastening the transient response and increasing the bandwidth.
Proportional–Integral compensation
Proportional-integral (PI) compensators (35.50) are used to guarantee null steady-state error with acceptable rise times. The PI compensators are a particular case of lag-lead compensators, therefore suitable for converters with good stability margin but poor steady-state accuracy:
CPI(s)=1+sTzsTp=TzTp+1sTp=Kp+Kis=Kp(1+ΚiKps)=Kp(1+1sTz)=1+sTzsTz/Kp
Proportional–integral plus high-frequency pole compensation
This integral plus zero-pole compensation (35.51) combines the advantages of a PI with lead or lag compensation. It can be used in converters with good stability margin but poor steady-state accuracy. If the frequencies 1/TM and 1/Tz (1/Tz<1/TM) are carefully chosen, compensation lowers the loop gain at high frequency while only slightly lowering the phase to achieve the desired phase margin:
CILD(s)=1+sTzsTp(1+sTM)=TzTpTMs+1/Tzs(s+1/TM)=Wcps+ωzs(s+ωM)
Proportional-integral derivative (PID), plus high-frequency poles
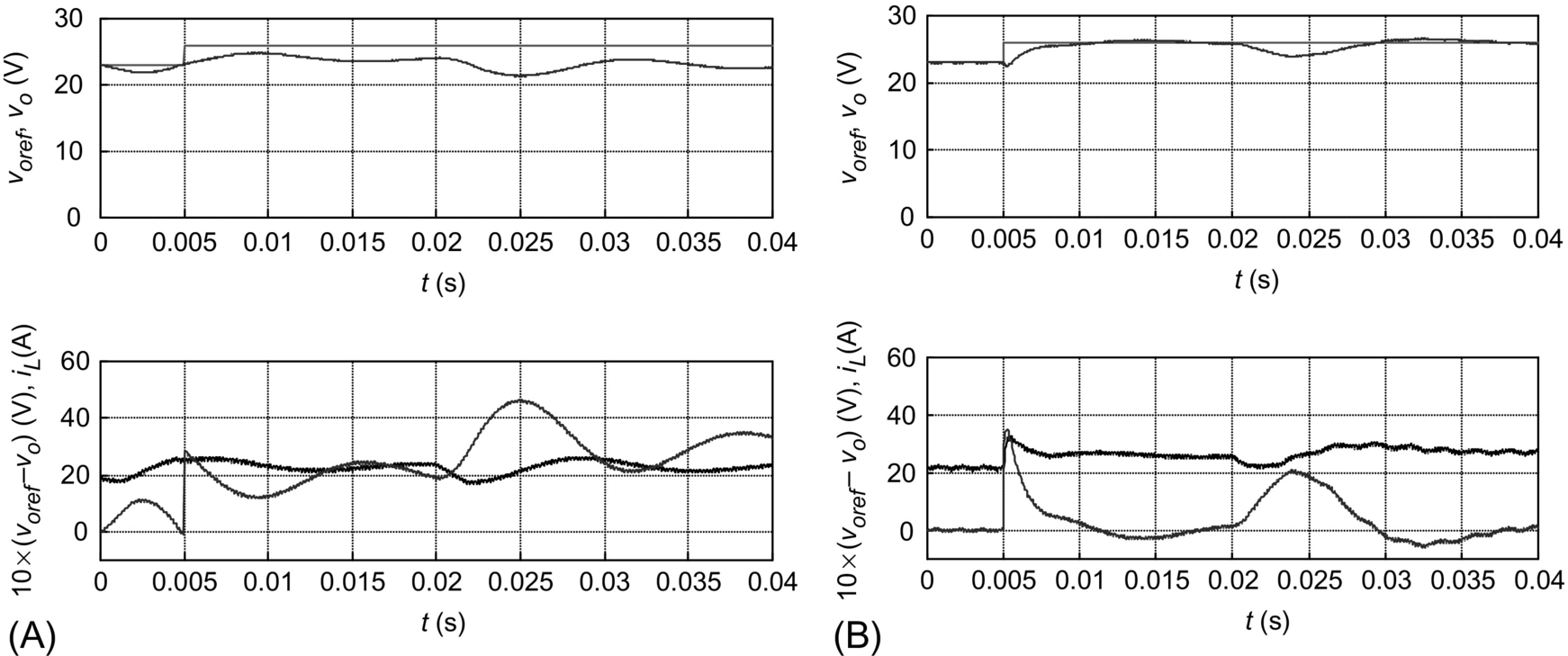
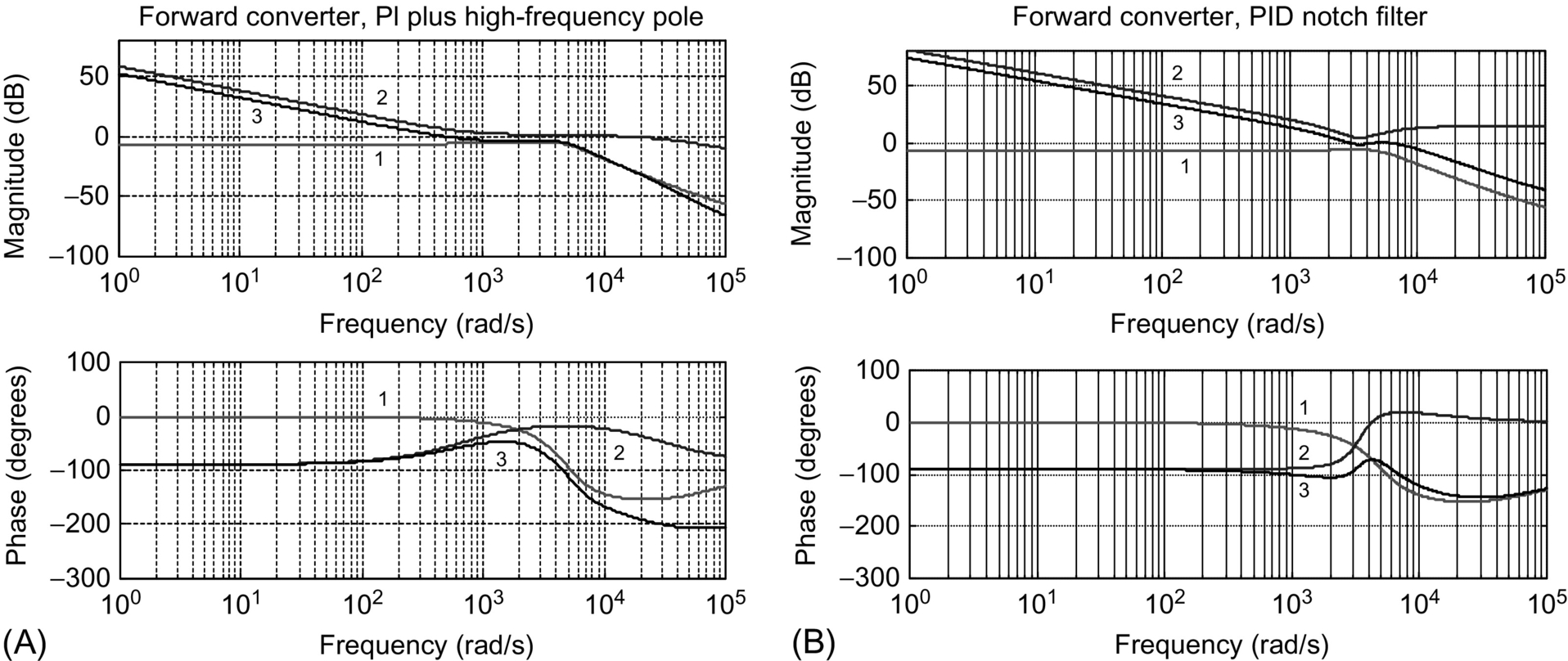
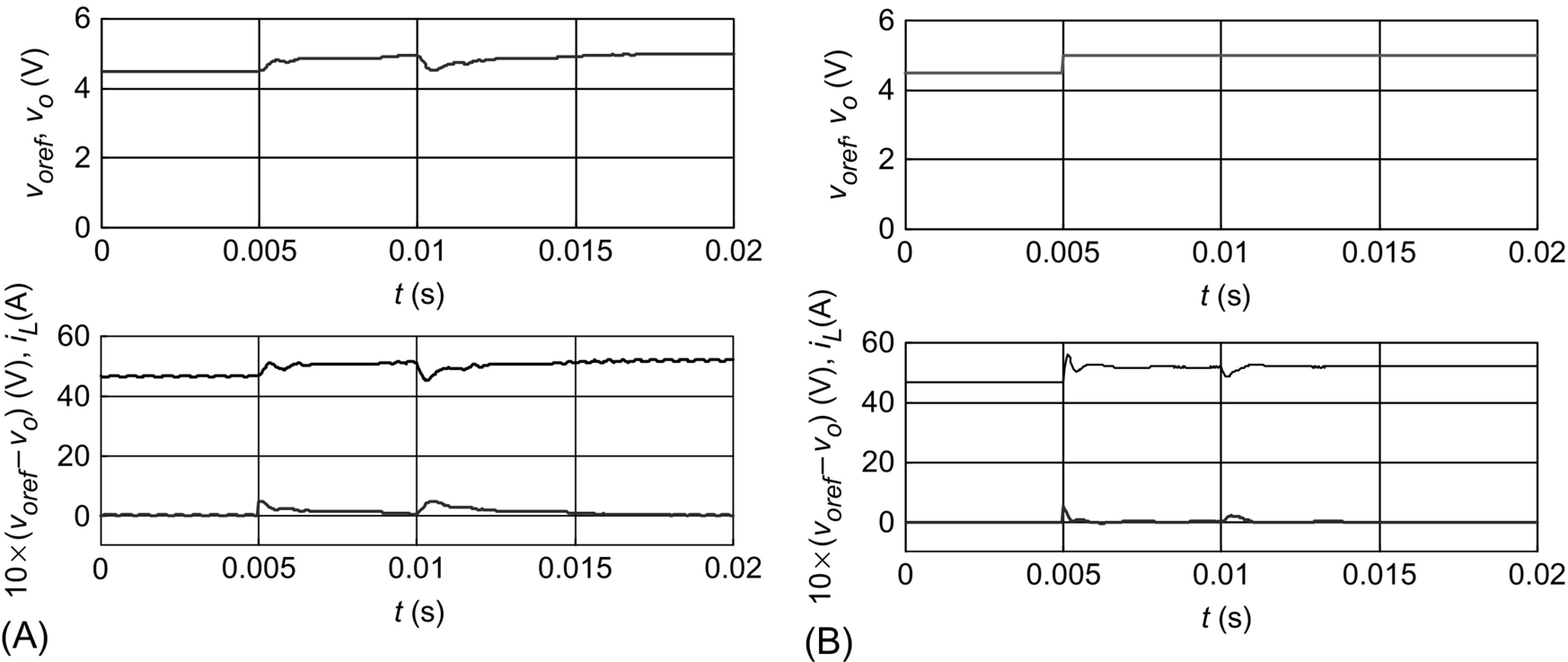
The PID notch filter type (35.52) scheme is used in converters with two lightly damped complex poles, to increase the response speed, while ensuring zero steady-state error. In most switching power converters, the two complex zeros are selected to have a damping factor greater than the converter complex poles and slightly smaller oscillating frequency. The high-frequency pole is placed to achieve the needed phase margin [9]. The design is correct if the complex pole loci, heading to the complex zeros in the system root locus, never enter the right half plane:
CPIDnf(s)=Tcps2+2ξcpω0cps+ω20cps(1+s/ωp1)=Tcps1+s/ωp1+2Tcpξcpω0cp1+s/ωp1+Tcpω20cps(1+s/ωp1)=Tcps1+s/ωp1+Tcpω20pc(1+2sξcp/ω0cp)s(1+s/ωp1)
For systems with a high-frequency zero placed at least one decade above the two lightly damped complex poles, the compensator (35.53), with ωz1≈ωz2<ωp, can be used. Usually, the two real zeros present frequencies slightly lower than the frequency of the converter complex poles. The two high-frequency poles are placed to obtain the desired phase margin [9]. The obtained overall performance will often be inferior to that of the PID type notch filter:
CPID(s)=Wcp(1+s/ωz1)(1+s/ωz2)s(1+s/ωp)2
35.2.5.2 Compensator Selection and Design
The procedure to select the compensator and to design its parameters can be outlined as follows:
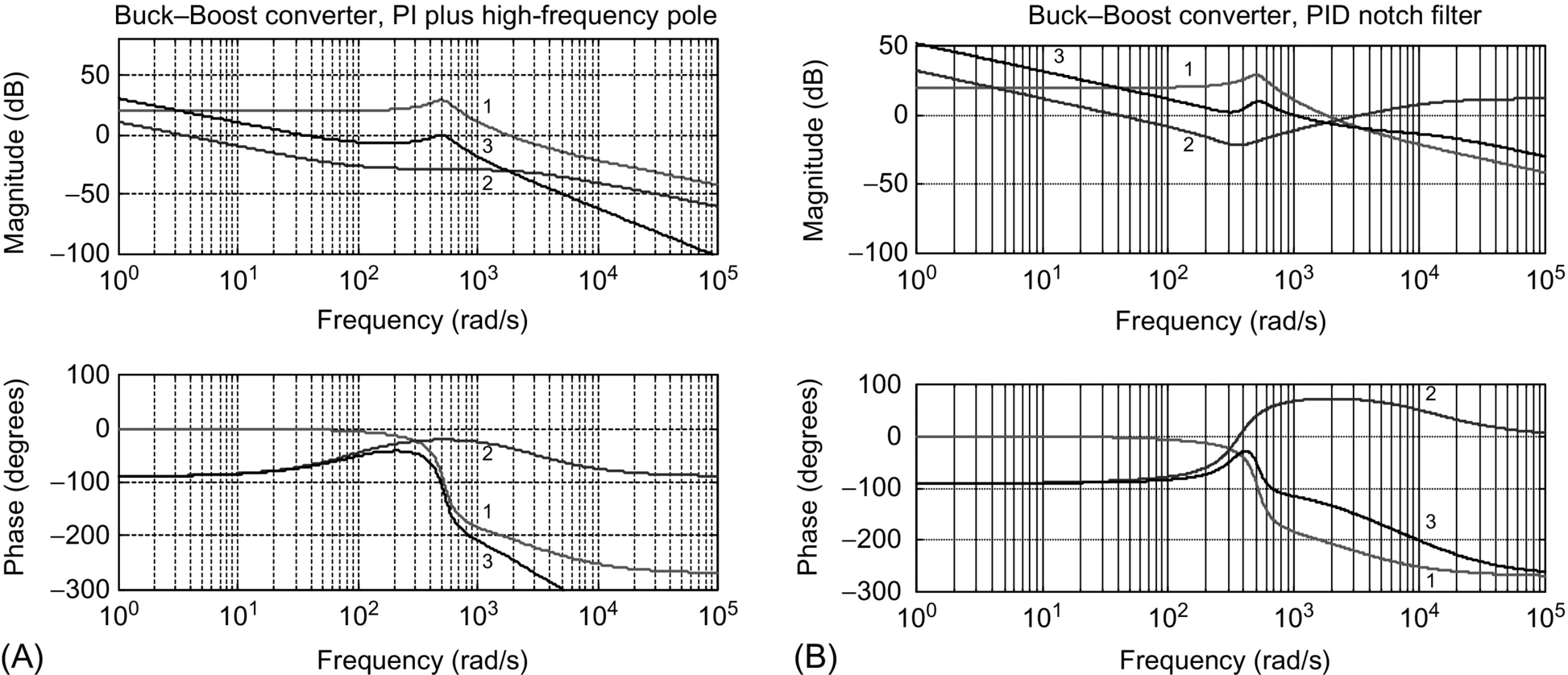
1. Compensator selection: In general, since VDC perturbations exist, null steady-state error guarantee is needed. High-frequency poles are usually necessary, if the transfer function shows a −6 dB/octave roll-off due to high-frequency left plane zeros. Therefore, in general, two types of compensation schemes with integral action (35.51) or (35.50) and (35.52) or (35.53) can be tried. Compensator (35.52) is usually convenient for systems with lightly damped complex poles.
2. Unity gain frequency ω0dB choice:
• If the selected compensator has no complex zeros, it is better to be conservative, choosing ω0dB sufficiently below the frequency of the lightly damped poles of the converter (or the frequency of the right half-plane zeros if lower). However, because of the resonant peak of most converter transfer functions, the phase margin can be obtained at a frequency near the resonance. If the phase margin is not enough, the compensator gain must be lowered.
• If the selected compensator has complex zeros, ω0dB can be chosen slightly above the frequency of the lightly damped poles.
3. Desired phase margin (φM) specification φM≥30° (preferably between 45 and 70°).
4. Compensator zero-pole placement to achieve the desired phase margin:
• With the integral plus zero-pole compensation type (35.51), the compensator phase φcp, at the maximum frequency of unity gain (often ω0dB), equals the phase margin (φM) minus 180° and minus the converter phase φcv,(φcp=φM−180°−φcv). The zero-pole position can be obtained calculating the factor fct=tg (π/2+ φcp/2) being ωz=ω0dB/fct and ωM=ω0dBfct.
• With the PID notch filter type (35.52) controller, the two complex zeros are placed to have a damping factor ξp roughly equal to two times the damping ξz of the converter complex poles and oscillating frequency ω0cp 30% smaller than the complex poles frequency ωp. The high-frequency pole ωp1 is placed to achieve the needed phase margin (ωp1≈(ω0cp·ω0dB)1/2fct2 with fct=tg (π/2+φcp/2) and φcp=φM−180°−φcv [5]). Alternatively, since for stability ξz ω0cp>ξp ωp and ωp√1−ξ2p>ω0cp√1−ξ2z![]() , it is obtained 1>ξz>ξp and using the geometric mean, ω0cp=ωp√ξpξz√1−ξ2p1−ξ2z
, it is obtained 1>ξz>ξp and using the geometric mean, ω0cp=ωp√ξpξz√1−ξ2p1−ξ2z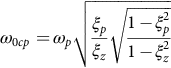 .
.
5. Compensator gain calculation (the product of the converter and compensator gains at the ω0dB frequency must be one).
6. Stability margin verification using Bode plots and root locus.
7. Result evaluation. Restarting the compensator selection and design, if the attained results are still not good enough.
Note that several modern computer programs, such as MATLAB, provide very easy and efficient tools (such as SISOTOOL) to design these controllers, even considering that switching power converters are discrete systems. Optimum controllers such as linear-quadratic-Gaussian (LQG, LQR) controllers, whose performances might be much better than linear controllers, can also be designed using the same tools. However, in evaluating optimum controller results, care must be taken in order to guarantee that the controlled converter frequency bandwidth and gain are not beyond the validity limits of the used models.