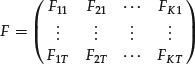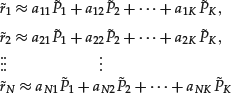Factor Models

GUOFU ZHOU, PhD

Frederick Bierman and James E. Spears Professor of Finance, Olin Business School, Washington University in St. Louis

FRANK J. FABOZZI, PhD, CFA, CPA

Professor of Finance, EDHEC Business School

Given a set of assets or asset classes, an important task in the practice of investment management is to understand and estimate their expected returns and the associated risks. Factor models are widely used by investors to link the risk exposures of the assets to a set of known or unknown factors. The known factors can be economic or political factors, industry factors or country factors, and the unknown factors are those that best describe the dynamics of the asset returns in the factor models, but they are not directly observable or easily interpreted by investors and have to be estimated from the data.

Applications of the mean-variance analysis and portfolio selection theories in general require the estimation of expected asset returns and their covariance matrix. Those market participants who can identify those true factors that drive asset returns should have much better estimates of the true expected asset returns and the covariance matrix, and hence should be able to form a much better portfolio than otherwise possible. Hence, a lot of research and resources are devoted to analyzing factor models in practice by the investment community. There is an intellectual “arms race” to find the best portfolio strategies to outperform competitors.

Factor model estimation depends crucially on whether the factors are identified (known) and unidentified (latent), and depend on the sample size and the number of assets. In addition, factor models can be used not only for explaining asset returns, but also for predicting future returns. In this entry, we review first the factor models in the case of known and latent factors in order to provide a big picture, and then discuss the details of estimation.

ARBITRAGE PRICING THEORY

One of the fundamental problems in finance is to explain the cross-section differences in asset expected returns. Specifically, what factors can explain the observed differences? Those factors that systematically affect the differences in expected returns are therefore the risks that investors are compensated for. Hence, the term “factors” is interchangeable with the term “risk factors.”

The arbitrage pricing theory (APT), formulated by Ross (1976), posits that expected returns of assets are linearly related to K systematic factors, and the exposure to these factors is measured by factor betas; that is,

(1)

where is the beta or risk exposure on the k-th factor, and γk is the factor risk premium, for k = 1, 2, … , K.

Technically, the APT assumes a K-factor model for the return-generating process, that is, the asset returns are influenced by K factors in the economy via linear regression equations,

(2)

where are the systematic factors that affect all the asset returns on the left-hand side, i = 1, 2, … , N; and is the asset specific risk. Note that we have placed a tilde sign (∼) over the random asset returns, factors, and specific risks. By so doing, we distinguish between factors (random) and their realizations (data), which are important for understanding the estimation procedure below.

Theoretically, under the assumption of no arbitrage, the asset pricing relation of the APT as given by equation (1) must be true as demonstrated by Ross. There are two important points to note. First, the return-generating process as given by equation (2) is fundamentally different from the asset pricing relation. The return-generating process is a statistical model used to measure the risk exposures of the asset returns. It does not require drawing any economic conclusion, nor does it says anything about what the expected returns on the assets should be. In other words, the αi’s in the return-generating process can statistically be any numbers. Only when the no-arbitrage assumption is imposed can one claim the APT, which says that the αi’s should be linearly related to their risk exposures (betas).

Second, the APT does not provide any specific information about what the factors are. Nor does the theory make any claims on the number of factors. It simply assumes that if the returns are driven by the factors, and if the smart investors know the betas (via learning or estimating), then an arbitrage portfolio, which requires no investment but yields a positive return, can be formed if the APT pricing relation is violated in the market. Hence, in equilibrium if there are no arbitrage opportunities, we should not observe deviations from the APT pricing relation.

TYPES OF FACTOR MODELS

In this section we describe the different types of factor models.

Known Factors

The simplest case of factor models is where the K factors are assumed known or observable, so that we have time-series data on them. In this case, the K-factor model for the return-generating process as given by equation (2) is a multiple regression for each asset and is a multivariate regression if all of the individual regressions are pooled together. For example, if one believes that the gross domestic product (GDP) is the driving force for a group of stock returns, one would have a one-factor model,

The above equation corresponds to equation (1) with K = 1 and . In practice, one can obtain time-series data on both the asset returns and GDP, and then one can estimate regressions to obtain all the parameters, including in particular the expected returns.

Another popular one-factor model is the market model regression

where is the return on a stock market index.

To understand the covariance matrix estimation, it will be useful to write the K-factor model in matrix form,

or

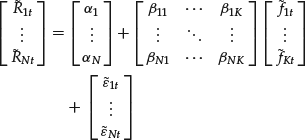
where

= an N-vector of asset excess returns
= an N-vector of the alphas
= an N × K of betas or factor loadings
= a K-vector of the factors
= an N-vector of the model residuals.

For example, we can write a model with N = 3 assets and K = 2 factors as

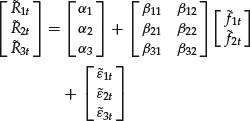
Taking covariance on both sides of equation (2), we have the return covariance matrix

(3)

where is the covariance matrix of the factors, and is the covariance matrix of the residuals. can be estimated by using the sample covariance matrix from the historical returns. This works for too if N is small relative to T. However, when N is large relative to T, the sample covariance matrix of the residuals will be poorly behaved.

Usually an additional assumption that the residuals are uncorrelated is imposed, so that becomes a diagonal matrix and can then be estimated by using the sample variances of the residuals. Plugging in the estimates of all the parameters into the right-hand side of equation (3), we obtain the covariance matrix needed for applying mean-variance portfolio analysis.

In the estimation of a multifactor model, it is implicitly assumed that the number of time series observations T is far greater than K, the number of factors. Otherwise, the regressions will perform poorly. For the case in which K is close to T, some special treatments are needed. This will be addressed later in this entry.

Examples of Multifactor Models with Known Factors

Before discussing latent factors, let’s briefly describe four multifactor models where known factors are used: (1) the Fama-French three-factor model (Fama and French, 1993), (2) the MSCI Barra fundamental factor model, (3) the Burmeister-Ibbotson-Roll-Ross (BIRR) macro-economic factor model (Burmeister, Roll, and Ross, 1994), and (4) the Barclay Group Inc. factor model. The first three are equity factor models and the last is a bond factor model.

The widely used Fama-French three-factor model is a special case of equation (1) with K = 3,

where , as before, is the return on a stock market index, and are two additional factors. SMBt (small minus big) is defined as the difference between the returns on diversified portfolios of small and big stocks (where small and big are measured in terms of stock market capitalization), and HMLt (high minus low) is defined as the difference between the returns on diversified portfolios of high and low book value-to-market value (B/M) stocks. The introduction of these factors by Fama and French is to better capture the systematic variation in average return for typical portfolios than when using a stock market index alone. These factors are supported by empirical studies and are consistent with classifying stocks in terms of growth and value.

Fundamental factor models use company and industry attributes and market data as “descriptors.” Examples are price/earnings ratios, book/price ratios, estimated earnings growth, and trading activity. The estimation of a fundamental factor model begins with an analysis of historical stock returns and descriptors about a company. In the MSCI Barra model, for example, the process of identifying the factors begins with monthly returns for hundreds of stocks that the descriptors must explain. Descriptors are not the “r factors” but instead they are the candidates for risk factors. The descriptors are selected in terms of their ability to explain stock returns. That is, all of the descriptors are potential risk factors but only those that appear to be important in explaining stock returns are used in constructing risk factors. Once the descriptors that are statistically significant in explaining stock returns are identified, they are grouped into “risk indexes” to capture related company attributes. For example, descriptors such as market leverage, book leverage, debt-to-equity ratio, and company’s debt rating are combined to obtain a risk index referred to as “leverage.” Thus, a risk index is a combination of descriptors that captures a particular attribute of a company. For example, in the MSCI Barra fundamental multifactor model, there are 13 risk indices and 55 industry groups. The 55 industry classifications are further classified into sectors.

In a macroeconomic factor model, the inputs to the model are historical stock returns and observable macroeconomic variables. In the BIRR macroeconomic multifactor model, the macro-economic variables that have been pervasive in explaining excess returns and which are therefore included in the market are

• The business cycle: Changes in real output that are measured by percentage changes in the index of industrial production.
• Interest rates: Changes in investors’ expectations about future interest rates that are measured by changes in long-term government bond yields.
• Investor confidence: Expectations about future business conditions as measured by changes in the yield spread between high- and low-grade corporate bonds.
• Short-term inflation: Month-to-month jumps in commodity prices, such as gold or oil, as measured by changes in the consumer price index.
• Inflationary expectations: Changes in expectations of inflation as measured by changes in the short-term, risk-free nominal interest rate.

Additional variables, such as the real GDP growth and unemployment rates, are also among the macroeconomic factors used by asset managers in other macroeconomic multifactor models. Moreover, some asset managers also have identified technical variables, such as trading volume and market liquidity, as factors.

The Barclay Group Inc. (BGI) bond factor model (previously the Lehman bond factor model) uses two categories of systematic risk factors: term structure factors and non–term structure risk factors. The former include changes in the level of interest and changes in the shape of the yield curve. The non–term structure factors are sector risk, credit risk, optionality risk, and a series of risks associated with investing in mortgage-backed securities.

The search for factors is a never-ending task of asset managers. In practice, many popular investment software packages use dozens of factors. Some academic studies, such as Ludvigson and Ng (2007), use hundreds of them.

Latent Factors

While some applications use observed factors, some use entirely latent factors, that is, the view that the factors ft in the K-factor model,

are not directly observable. An argument for the use of latent factors is that the observed factors may be measured with errors or have been already anticipated by investors. Without imposing what ft are from our likely incorrect belief, we can statistically estimate the factors based on the factor model and data.

It is important to understand that in the field of statistics, there is statistical methodology known as “factor analysis” and the model generated is referred to as a “factor model.” Factor models as used by statisticians are statistical models that try to explain complex phenomena through a small number of basic causes or factors with the factors being latent. Factor models as used by statisticians serve two main purposes: (1) They reduce the dimensionality of models to make estimation possible, and/or (2) they find the true causes that drive data. In our discussion of multifactor models, we are using the statistical tool of factor analysis to try to determine the latent factors driving asset returns.

While the estimation procedures for determining the set of factors will be discussed in the next section, it will be useful to know some of the properties of the factor model here. The first property is that the factors are not uniquely defined in the model, but all sets of factors are linear combinations of each other. This is because if is a set of factors, then, for any K × K invertible matrix A, we have

(4)

which says that if with regression coefficients (known as adding factor loadings in the context of factor models) explains asset returns well, so does with loadings . The linear transformation of , , is also known as a rotation of ft.

The second property is that we can assume all the factors have zero mean (i.e., ). This is because if , then the factor model can be written as

(5)

If we rename as the new alphas, and as the new factors, then the new factors will have zero means, and the new factor model is statistically the same as the old one. Hence, without loss of generality, we will assume that the mean of the factors are zeros in our estimation in the next section.

Note that the return covariance matrix formula, equation (3) or

(6)

holds regardless of whether the factors are observable or latent. However, through factor rotation, we can make a new set of factors so as to have the identity covariance matrix. In this case with , we say that the factor model is standardized, and the covariance equation then simply becomes

(7)

In general, can have nonzero off-diagonal elements, implying that the residuals are correlated. If we assume that the residuals are uncorrelated, then becomes a diagonal matrix, and the factor model is known as a strict factor model. If we assume further that has equal diagonal elements, i.e., for some with IN an N identity matrix, then the factor model is known as a normal factor model.

Both Types of Factors

Rather than taking the view of only observable factors or only latent factors, we can consider a more general factor model with both types of factors,

(8)

where is a K-vector of latent factors, is an L-vector of observable factors, and are the betas associated with . This model makes intuitive sense. If we believe a few fundamental or macroeconomic factors are the driving forces, they can be used to create the vector. Since we may not account for all the possible factors, we need to add K unknown factors, which are to be estimated from the data.

The estimation of the above factor model given by equation (8) usually involves two steps. In the first step, a regression of the asset returns on the known factors is run in order to obtain , an estimate of . This allows us to compute the residuals,

(9)

that is, the difference of the asset returns from their fitted values by using the observed factors for all the time periods. Then, in the second step, a factor estimation approach is used to estimate the latent factors for ,

(10)

where is the random differences whose realized values are . The estimation method for this model is the same as estimating a latent factor model and will be detailed in the next section. With the factor estimates, we can treat the latent factors as known, and then use equation (8) to determine the expected asset returns and covariance matrix.

Predictive Factor Models

An important feature of factor models is that they use time t factors to explain time t returns. This is to estimate the long-run risk exposures of the assets, which are useful for both risk control and portfolio construction. On the other hand, portfolio managers are also very concerned about time-varying expected returns. In this case, they often use a predictive factor model such as the following to forecast the returns,

(11)

where as before and are the latent and observable factors, respectively. The single difference is that the earlier is now replaced by . Equation (11) uses time t factors to forecast future return .

Computationally, the estimation of the predictive factor model is the same as for estimating the standard factor models. However, it should be emphasized that the regression R2, a measure of model fitting, is usually very good in the explanatory factor models. In contrast, if a predictive factor model is used to forecast the expected returns of various assets, the R2 rarely exceeds 2%. This simply reflects the fact that assets returns are extremely difficult to predict in the real world. For example, Rapach, Strauss, Tu, and Zhou (2009) find that that the R2 are mostly less than 1% when forecasting industry returns using a variety of past economic variables and past industry returns.

FACTOR MODEL ESTIMATION

In this section, we provide first a step-by-step procedure for estimating the factor model based on the popular and implementable approach, principal components analysis (PCA), to which a detailed and intuitive introduction is provided in the last section of this entry. PCA is a statistical tool that is used by statisticians to determine factors with statistical learning techniques when factors are not observable. That is, given a variance-covariance matrix, a statistician can determine factors using the technique of PCA. Then, after learning the computational procedure, we provide an application to identify three factors for bond returns. Finally, we outline some alternative procedures for estimating the factor models and their extensions.

Computational Procedure

By our use of latent models, we need to consider only how to estimate the latent factors from the K-factor model,

(12)

where

This version of the factor model is obtained in two steps. We de-mean first the factor ft so that the alphas are the expected returns of the assets. Second, we de-mean again the asset returns. In other words, we let .

In practice, suppose that we have return data on N risky assets over T time periods. Then the realizations of the random variable can be summarized by a matrix,

(13)

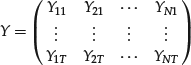
where each row is the N asset returns subtracting from their sample means at time t for t = 1, 2, … , T. Our task is to estimate the realizations (unobserved) on the K factors, , over the T periods,

(14)

We will now apply PCA estimation methodology.

There are two important cases, each of which calls for a different way of applying PCA. The first case is the one of traditional factor analysis in which N is treated as fixed, and T is allowed to grow. We will refer to this case as the “fixed N” below. The second case is when N is allowed to grow but T is either fixed or allowed to grow. We will refer to this case simply as “large N.”

Case 1: Fixed N

In the case of fixed N, we have a relatively smaller number of assets and a relatively large sample size. Then the covariance matrix of the asset returns, which is the same as the covariance matrix of , can be estimated by the sample covariance matrix,

(15)

which is an N by N matrix since Y is T by N. For example, if we think there are K (say K = 5) factors, we can use standard software to compute the first K eigenvectors of corresponding to the first K largest eigenvalues of , each of which is an N vector. Let be the N by K matrix formed by these K eigenvectors. Then will be an estimate of . Based on this, the factors are estimated by

(16)

where Yt is the t-th row of Y, and is the estimate of ft, the t-th row of F. The ’s are the estimated realizations of the first K factors. Seber (1984) explains why the ’s are good estimates of the true and unobserved factor realizations. However, theoretically, they, though close, will not necessarily converge to the true values, unless the factor model is normal, as T increases. Nevertheless, despite this problem, this procedure is widely used in practice.

Case 2: Large N

In the case of large N, we have a large number of assets. We now form a new matrix based on the product of Y with ,

(17)

which is a T by T matrix since Y is T by N. Given K, we use standard software to compute the first K eigenvectors of corresponding to the first K largest eigenvalues of , each of which is a T vector. Letting be the T by K matrix formed by these K eigenvectors, the PCA says that is an estimate of the true and unknown factor realizations F of equation (14), up to a linear transformation. Connor and Korajczyk (1986) provided the first study in the finance literature to apply the PCA as described above. The method is also termed “asymptotic PCA” since it allows the number of assets to increase without bound. In contrast, traditional PCA keeps N fixed, while allowing the number of time periods, T, to be large.

Theoretically, if the true factor model is the strict factor model or is not much too different from it (i.e., the residual correlations are not too strong), Bai (2003) shows that converges to F up to a linear transformation when both T and N increase without limit. The estimation errors are of order the larger of 1/T or , and converge to zero as both T and N grow to infinity. However, when T is fixed, we need a stronger assumption that the the true factor model is close to a normal model, then the estimation errors are of order of . Intuitively, at each time t, given that there are only a few factors to pricing so many assets, we should have enough information to back out the factors accurately.

Based on the estimated factors, the factor loadings are easily estimated from equation (12). For example, we can obtain the loadings for each asset by estimating the standard ordinary least squares (OLS) regression of the asset returns on the factors. Mathematically, this is equivalent to computing all the loadings from the formula

(18)

Under the same conditions above, also converges to up to a linear transformation.

The remaining question is how to determine K. In practice, this may be determined by trial and error depending on how different K’s perform in model fitting and in meeting the objectives where the model is applied. From an econometrics perspective, there is a simple solution in Case 2. Bai and Ng (2002) provide a statistical criterion

(19)

where

(20)

For a given K, V(K) is the sum of the fitted squared residual errors of the factor model across both asset and time. This is a measure of model fitting. The smaller the V(K), the better the K-factor model in explaining the asset returns. So we want to choose such a K that minimizes V(K). However, the more the factors, the smaller the V(K), but at a cost of estimating more factors with greater estimation errors. Hence, we want to penalize too many factors. This is the same as the case in linear regressions where we also want to penalize too many regressors. The second term in equation (19) plays this role. It is an increasing function of K. Therefore, the trade-off between model fitting and estimation errors requires us to minimize the IC(K) function. Theoretically, assuming that the factor model is indeed true for some fixed K*, Bai and Ng show that the K that minimizes IC(K) will converge to K* as either N or T or both increase to infinity.

An Application to Bond Returns

To illustrate the procedure, consider an application of the PCA factor analysis to the excess returns on Treasury bonds with maturities 12, 18, 24, 30, 36, 42, 48, 54, 60, 120, and beyond 120 months. Hence, there are N = 11 assets. With monthly data from January 1980 to December 2008, available from the Center for Research in Security Prices of the University of Chicago’s Graduate School of Business, we have a sample size of T = 348. Since N is small relative to T, this is a case of the fixed N.

Now

is an 11 by 11 matrix. We can easily compute its eigenvalues and eigenvectors. The largest three eigenvalues are

whose sum is more than 99% of the sum of all the eigenvalues. Thus, it is enough to consider K = 3 factors and use the first three eigenvectors, PCAs, as proxies for the factors. Denote them as F1, F2 and F3.

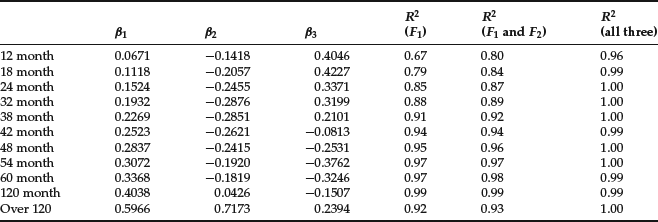
Table 1 Factor Loadings and Explanatory Power

Consider now the regression of the 11 excess bond returns on the three factors,

where i = 1, 2, … , 11. The regression R2s of using all the factors for each of the assets are reported in the last column of Table 1. All but one is 99% or above, confirming the eigenvalue analysis that three factors are sufficient, which explains almost all the variations of the bond returns. However, when only the first two are used, the R2s are smaller, but the minimum is still over 80%. When only the first factor is used, the R2s range from 67% on the first bond return to 99% on the 10th. Overall, the PCA factors are effective in explaining the asset returns.

The factor loadings or regression coefficients on the factors are also reported in Table 1. It is interesting that the loadings on the first factor are all positive. This implies that a positive realization of F1 will have a positive effect on the returns of all the bonds. It is, however, clear that F1 affects long-term bonds more than short-term bonds. As an approximation, F1 is usually interpreted as a level effect or parallel effect that roughly shifts the returns on bonds across maturity.

The second factor, however, has a different pattern from the first. A positive realization of F1 will have a negative effect on short-term bonds and a positive effect on the long-term ones. This is equivalent to an increase in the slope of the bond returns across maturity (known as yield curve). Therefore, F2 is commonly identified as a steepness factor.

Finally, a positive realization of F3 will have a positive effect on both short- and long-term bonds, but a negative effect on the intermediate ones. Hence F3 is usually interpreted as a curvature factor. Litterman and Scheinkman (1991) appears to have been one of the first to to apply the PCA to study bond returns and to have identified the above three factors. Although the data we used here are different, the three factors we computed share the same properties as those identified by them.

Alternative Approaches and Extensions

The standard statistical approach for estimating the factor model is the maximum likelihood (ML) method. Consider the factor model given by equation (12) where , . The de-meaned returns and standardized factors are usually assumed to have normal distributions.

In addition, the factors are usually standardized so that , and the residuals are assumed uncorrelated so that is diagonal. Then the log likelihood function, as the log density function of the returns, is

(21)

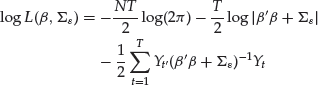
The ML estimator of the parameters and are those values that maximize the log likelihood function. Since enters into the function in a complex nonlinear way, an analytical solution to the maximization problem is a very difficult problem. Numerically, it is still difficult if maximizing directly.

There is, however, a data-augmentation technique known as the expectation maximization (EM) algorithm that can be applied (see Lehmann and Modest, 1998). The EM algorithm can be effective in numerically solving the earlier maximization problem. The idea of the EM algorithm is simple. The key difficulty here is that the factors are unobserved. But conditional on the parameters and the factor model, we can learn them. Consider now that given the factors , the log likelihood function conditional on ft is

(22)

Because it is conditional on ft, the factor model is the usual linear regression. In other words, integrating out ft from equation (22) yields the unconditional . The beta estimates conditional on ft are straight-forward. They are the usual OLS regression coefficients, and the estimates for are the residual variances.

On the other hand, conditional on the parameters, we can learn the factors by using their conditional expected values obtained easily from their joint distribution with the returns. Hence, we can have an iterative algorithm. Starting from an initial guess of the factors, we maximize the conditional likelihood function to obtain the OLS and estimates, which is the M-step of the EM algorithm. Based on these estimates, we update a new estimate of ft using their expected value. This is the EM algorithm’s E-step. Using the new ft, we learn new estimates of and in the M-step. With the new estimates, we can again update the ft. Iterating between the EM steps, the limits converge to the unconditional ML estimate and the factor estimates converge to the true ones.

As an alternative to the ML method, Geweke and Zhou (1996) propose a Bayesian approach, which treats all parameters as random variables. It works in a way similar to the EM algorithm. Conditional on parameters, we learn the factors, and conditional on the factors, we learn the parameters. Iterating after a few thousand times, we learn the entire joint distribution of the factors and parameters, which are all we need in a factor model. The advantage of the Bayesian approach is that it can incorporate prior information and can provide exact inference. In contrast, the ML method cannot use any priors, nor can it obtain the exact standard errors of both parameters and functions of interest due to the complexity of the factor model. Nardari and Scruggs (2007) extend the Bayesian approach to allow a more general model in which the covariance matrix can vary over time and the APT restrictions can be imposed.

Finally, we provide two important extensions of the factor model that are useful in practice. Note that the factors we discussed thus far assume identical and independently distributed returns and factors. These are known as static factor models. The first extension is dynamic factor models, which allow the factors to evolve over time according to a vector autoregression,

(23)

where the A’s are the regression coefficient matrices, m is the order of the autoregression that determines how far past factor realizations still affect today’s realizations, and vt is the residual. In practice, many economic variables are highly persistent, and hence it will be important to incorporate this as above. (See Amengual and Watson [2007] for a discussion of estimation for dynamic factor models.)

The second extension is to allow the case with a large number of factors. Consider our earlier factor model

(24)

where is a K vector of latent factors, is an L vector of observable factors. The problem now is that L is large, about 100 or 200, for instance. This requires at least a few hundred or more time series observations for the regression of Rt on gt to be well behaved, and this can cause a problem due to the lack of long-term time series data or due to concerns of stationarity. The idea is to break into two sets, and , with the first having a few key variables and the second having the rest. We then consider the modified model

(25)

where has a few variables too that represent a few major driving forces that summarize the potentially hundreds of variables of via another factor model,

(26)

where is the residual. This second factor model provides a large dimension reduction that transforms the hundreds of variables into a few, which can be estimated by the PCA. In the end, we have only a few factors in equation (25), making the analysis feasible based on the methods we discussed earlier. Ludvigson and Ng (2007) appear to be the first to apply such a model in finance. They find that the model can effectively incorporate a few hundred variables so as to make a significant difference in understanding stock market predictability.

USE OF PRINCIPAL COMPONENTS ANALYSIS

Principal components analysis (PCA) is a widely used tool in finance. It is useful not only for estimating factor models as explained in this entry, but also for extracting a few driving variables in general out of many for the covariance matrix of asset returns. Hence, it is important to understand the statistical intuition behind it. To this end, we provide a simple introduction to it in the last section of the entry.

Perhaps the best way to understand the PCA is to go through an example in detail. Suppose there are two risky assets, whose returns are denoted by and , with covariance matrix

That is, we assume that they have the same variances of 2.05 and covariance of 1.95. Our objective is to find a linear combination of the two assets so that it has a large component in the covariance matrix, which will be clear below. For notation brevity, we assume first that the expected returns are zeros; that is,

and will relax this assumption later.

Recall from linear algebra that we call any vector satisfying

an eigenvector of , and the associated the eigenvalue. In our example here, it is easy to verify that

and

so 4 and 0.1 are the eigenvalues, and and are the eigenvectors.

In practice, computer software is available to compute the eigenvalue and eigenvectors of any covariance matrix. The mathematical result is that for a covariance matrix of N assets, there are exactly N different eigenvectors and N associated positive eigenvalues (these eigenvalues can be equal in some cases). Moreover, the eigenvectors are orthogonal to each other; that is, their inner product or vector product is zero. In our example, it is clear that

It should be noted that the eigenvalue associated with each eigenvector is unique, but any scale of the eigenvector remains an eigenvector. In our example, it is obvious that a double of the first eigenvector, , is also an eigen-vector. However, the eigenvectors will be unique if we standardize them, making the sum of the elements 1. In our example,

are the standardized eigenvectors, which are obtained by scaling the earlier eigenvectors by . These are indeed standardized, since

Now let us consider two linear combinations (or portfolios without imposing the weights summing to 1) of the two assets whose returns are and ,

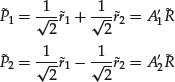
where . Both and are called the principal components (PCs). There are three important and interesting mathematical facts about the PCs.

• Fact 1. The variances of the PCs are exactly equal to the eigenvalues corresponding to the eigenvectors used to form the PCs.
  That is,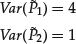

  

Note that the two PCs are random variables since they are the linear combination of random returns. So, their variances are well defined. The equalities to the eigenvalues can be verified directly.

• Fact 2. The returns can also be written as linear combinations of the PCs.

The PCs are defined as linear combinations of the returns. Inverting them, the returns are linear functions of the PCs, too. Mathematically, , and so . Since A is orthogonal, , thus . That is, we have

(26)

• Fact 3. The asset return covariance matrix can be decomposed as the sum of the products of eigenvalues with the cross products of eigenvectors.

Mathematically, it is known that

which is also easy to verify in our example. The economic interpretation is that the total risk profile of the two assets, as captured by their covariance matrix, is a sum of two components. The first component is determined by the first PC, and the second is determined by the second PC. In other words, in the return linear combinations, equation (26), if we ignore P2, we will get only , the first component in the covariance matrix decomposition, and only the second if we ignore P1. We obtain the entire if we ignore neither.

The purpose of the PCA is finally clear. Since 4 is 40 times as big as 0.1, the second component in the decomposition has little impact, and hence may be ignored. Then, ignoring , we can write the returns simply as, based on equation (26),

This says that we can reduce the analysis of and by analyzing simple functions of . In this example, the result tells us that the two assets are almost the same. In practice, there may be hundreds of assets. By using PCA, we can reduce the dimensionality of the problem substantially to an analysis of perhaps a few, say five, PCs.

In general, when there are N assets with return , computer software can be used to obtain the N eigenvalues and N standardized eigenvectors. Let be the N eigenvalues in decreasing order, and be the standardized eigenvector associated with , and A be an N × N matrix formed by the all the eigenvectors. Then, the i-th PC is defined as , all of which can be computed in matrix form,

(27)

The decomposition for is

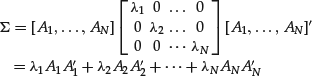
It is usually the case that, for some K, the first K eigenvalues are large, and the rest are too small and can then be ignored. In such situations, based on the first K PCs, we can approximate the asset returns by

(28)

In most studies, the K PCs may be interpreted as K factors that (approximately) derive the movements of all the N returns. Our earlier example is a case with K = 1 and N = 2.

In the above PCA discussion, the expected returns of the asset are assumed to be zero. If they are nonzero and given by a vector , will remain the same, and so will the eigenvalues and eigenvectors. However, in this case we need to replace all the ’s in equation (27) by ’s and add ’s on the right-hand side of equation (28). The interpretation will be, of course, the same as before.

In Case 1 of the factor model estimation (i.e., known or observable factors) discussed in the entry, the K PCs clearly provide a good approximation of the first K factors since they explain the asset variations the most given K. Moreover, in either Case 1 or Case 2 (latent factors), the PCA is equivalent to minimizing the model errors, as given by equation (20), by choosing both the loadings and factors, and hence the solution should be close to the true factors and loadings.

KEY POINTS

• The arbitrage pricing theory is a general multifactor model for pricing assets. The theory does not provide any specific information about what the factors are. Moreover, the APT does not make any claims on the number of factors either.
• The APT asserts that only taking the systematic risks is rewarded.
• The APT simply assumes that if the returns are driven by the factors, and if investors know the betas for the factors, then an arbitrage portfolio, which requires no investment but yields a positive return, can be formed if the APT pricing relation is violated in the market. In equilibrium, therefore, if there are no arbitrage opportunities, deviations from the APT pricing relation should not be observed.
• In practice, factor models are widely used as a tool for estimating expected asset returns and their covariance matrix. The reason is that if investors can identify the factors that drive asset returns, they will have much better estimates of the true expected asset returns and the covariance matrix, and hence will be able to form a much better portfolio than otherwise possible.
• Factor model estimation depends crucially on (1) whether the factors are identified (known) and unidentified (latent), and (2) the sample size and the number of assets. Furthermore, factor models can be used not only for explaining asset returns, but also for predicting future returns.
• The simplest case of factor models is where the factors are assumed to be known or observable, so that time-series data are those factors can be used to estimate the model.
• In practice there are three commonly used equity multifactor models where known factors are used: (1) the Fama-French three-factor model, (2) the MSCI Barra fundamental factor model, and (3) the Burmeister-Ibbotson-Roll-Ross macroeconomic factor model. Fundamental factor models use company and industry attributes and market data as descriptors. In a macroeconomic factor model, the inputs to the model are historical stock returns and observable macroeconomic variables.
• An argument for the use of latent factors is that the observed factors may be measured with errors or have been already anticipated by investors. Without imposing what the factors are from likely incorrect beliefs, asset managers can statistically estimate the factors based on the factor model and data.
• Two important extensions of the static factor model used in practice are (1) dynamic factor models, which allow the factors to evolve over time according to a vector autoregression, and (2) allowance for a large number of factors. This second factor model provides a large dimension reduction that transforms the hundreds of variables into a few, which can be estimated by principal components analysis.
• Principal components analysis is a simple statistical approach that can be applied to estimate a factor model easily and effectively.

REFERENCES

Amengual, D., and Watson, M. (2007). Consistent estimation of the number of dynamic factors in a large N and T panel. Journal of Business and Economic Statistics 25: 91–96.

Bai, J. (2003). Inferential theory for factor models of large dimensions. Econometrica 71: 135–172.

Bai, J., and Ng, S. (2002). Determining the number of factors in approximate factor models. Econometrica 70: 191–221.

Burmeister, E., Roll, R., and Ross, S. A. (1994). A practitioner’s guide to arbitrage pricing theory. In A Practitioner’s Guide to Factor Models (pp.). Charlottesville, VA, Institute of Chartered Financial Analysts.

Connor, G., and Korajczyk, R. (1986). Performance measurement with the arbitrage pricing theory: A new framework for analysis. Journal of Financial Economics 15: 373–394.

Fama, E. F., and French, K. R. (1993). Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33, 1: 3–56.

Geweke, J., and Zhou, G. (1996). Measuring the pricing error of the arbitrage pricing theory. Review of Financial Studies 9: 557–587.

Lehmann, B. N., and Modest, D. M. (1998). The empirical foundations of the arbitrage pricing theory. Journal of Financial Economics 21: 213–254.

Litterman, R., and Scheinkman, J. (1991). Common factors affecting bond returns. Journal of Fixed Income 1: 54–61.

Ludvigson, S. C., and Ng, S. (2007). The empirical risk-return relation: A factor analysis approach. Journal of Financial Economics 83: 171–222.

Nardari, F., and Scruggs, J. T. (2007). Bayesian analysis of linear factor models with latent factors, multivariate stochastic volatility, and APT pricing restrictions. Journal of Financial and Quantitative Analysis 42: 857–892.

Rapach, D. E., Strauss, J. K., Tu, J., and Zhou, G. (2009). Industry return predictability: Is it there out of sample? Working paper, Washington University, St. Louis.

Ross, S. A. (1976). The arbitrage theory of capital asset pricing. Journal of Economic Theory 13: 341–360.

Seber, G. A. F. (1984). Multivariate Observations, Wiley.