i
i
i
i
i
i
i
i
18 2. Miscellaneous Math
2.3 Trigonometry
In graphics we use basic trigonometry in many contexts. Usually, it is nothing too
fancy, and it often helps to remember the basic definitions.
2.3.1 Angles
Although we take angles somewhat for granted, we should return to their defini-
tion so we can extend the idea of the angle onto the sphere. An angle is formed
between two half-lines (infinite rays stemming from an origin) or directions, and
some convention must be used to decide between the two possibilities for the an-
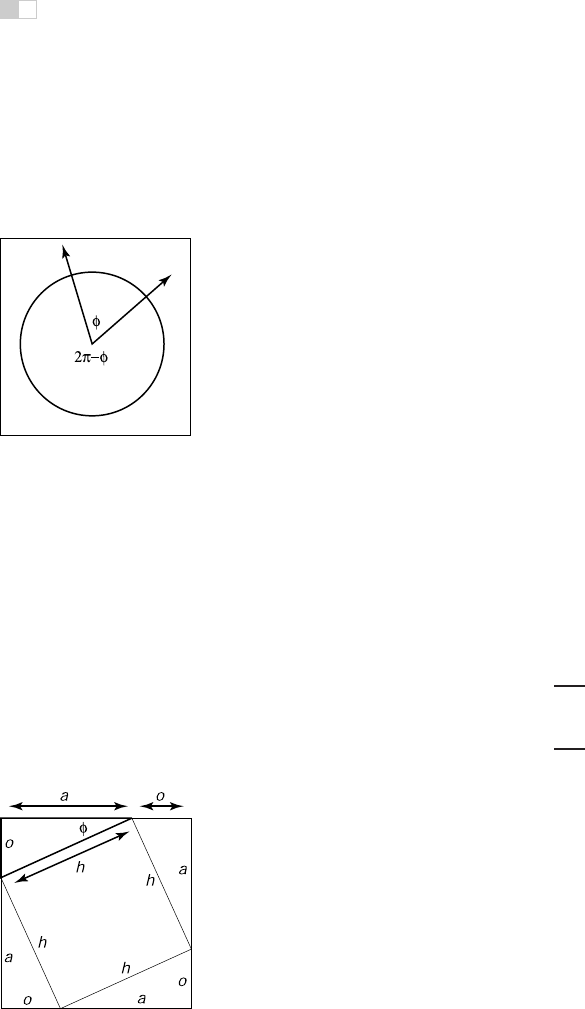
gle created between them as shown in Figure 2.6. An angle is defined by the
length of the arc segment it cuts out on the unit circle. A common convention is
that the smaller arc length is used, and the sign of the angle is determined by the
Figure 2.6. Two half-
lines cut the unit circle into
two arcs. The length of
either arc is a valid an-
gle “between” the two half-
lines. Either we can use the
convention that the smaller
length is the angle, or that
the two half-lines are spec-
ified in a certain order and
the arc that determines an-
gle φ is the one swept out
counterclockwise from the
first to the second half-line.
order in which the two half-lines are specified. Using that convention, all angles
are in the range [−π, π].
Each of these angles is the length of the arc of the unit circle that is “cut” by
the two directions. Because the perimeter of the unit circle is 2π, the two possible
angles sum to 2π. The unit of these arc lengths is radians. Another common unit
is degrees, where the perimeter of the circle is 360 degrees. Thus, an angle that is
π radians is 180 degrees, usually denoted 180
◦
. The conversion between degrees
and radians is
degrees =
180
π
radians;
radians =
π
180
degrees.
2.3.2 Trigonometric Functions
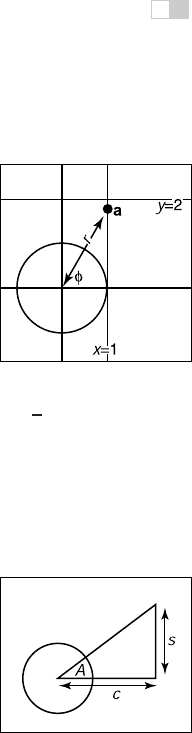
Given a right triangle with sides of length a, o,andh,whereh is the length of
the longest side (which is always opposite the right angle), or hypotenuse,an
important relation is described by the Pythagorean theorem:
a
2
+ o
2
= h
2
.
You can see that this is true from Figure 2.7, where the big square has area (a+o)
2
,
Figure 2.7. A geo-
metric demonstration of the
Pythagorean theorem.
the four triangles have the combined area 2ao, and the center square has area h
2
.
Because the triangles and inner square subdivide the larger square evenly,
we have 2ao + h
2
=(a + o)
2
, which is easily manipulated to the form above.
i
i
i
i
i
i
i
i
2.3. Trigonometry 19
We define sine and cosine of φ, as well as the other ratio-based trigonometric
expressions:
sin φ ≡ o/h;
csc φ ≡ h/o;
cos φ ≡ a/h;
sec φ ≡ h/a;
tan φ ≡ o/a;
cot φ ≡ a/o.
These definitions allow us to set up polar coordinates, where a point is coded
as a distance from the origin and a signed angle relative to the positive x-axis
(Figure 2.8). Note the convention that angles are in the range φ ∈ (−π, π],and
Figure 2.8. Polar coordi-
nates for the point (
x
a
,
y
a
)=
(1,
√
3) is (
r
a
, φ
a
)=(2,π/3).
that the positive angles are counterclockwise from the positive x-axis. This con-
vention that counterclockwise maps to positive numbers is arbitrary, but it is used
in many contexts in graphics so it is worth committing to memory.
Trigonometric functions are periodic and can take any angle as an argument.
For example sin(A)=sin(A +2π). This means the functions are not invertible
when considered with the domain R. This problem is avoided by restricting the
range of standard inverse functions, and this is done in a standard way in almost
all modern math libraries (e.g., (Plauger, 1991)). The domains and ranges are:
asin : [−1, 1] → [−π/2,π/2];
acos : [−1, 1] → [0,π];
atan : R → [−π/2,π/2];
atan2 : R
2
→ [− π, π].
(2.2)
The last function, atan2(s, c) is often very useful. It takes an s value proportional
Figure 2.9. The function
atan2(
s,c
) returns the angle
A
and is often very useful in
graphics.
to sin A and a c value that scales cos A by the same factor and returns A.The
factor is assumed to be positive. One way to think of this is that it returns the
angle of a 2D Cartesian point (s, c) in polar coordinates (Figure 2.9).
2.3.3 Useful Identities
This section lists without derivation a variety of useful trigonometric identities.
Shifting identities:
sin(−A)=−sin A
cos(−A)= cosA
tan(−A)=−tan A
sin(π/2 − A)= cosA
cos(π/2 − A)= sinA
tan(π/2 − A)= cotA

i
i
i
i
i
i
i
i
20 2. Miscellaneous Math
Pythagorean identities:
sin
2
A +cos
2
A =1
sec
2
A − tan
2
A =1
csc
2
A − cot
2
A =1
Addition and subtraction identities:
sin(A + B)=sinA cos B +sinB cos A
sin(A − B)=sinA cos B − sin B cos A
sin(2A)=2sinA cos A
cos(A + B)=cosA cos B −sin A sin B
cos(A − B)=cosA cos B +sinA sin B
cos(2A)=cos
2
A − sin
2
A
tan(A + B)=
tan A +tanB
1 − tan A tan B
tan(A − B)=
tan A − tan B
1+tanA tan B
tan(2A)=
2tanA
1 − tan
2
A
Half-angle identities:
sin
2
(A/2) = (1 − cos A)/2
cos
2
(A/2) = (1 + cos A)/2
Product identities:
sin A sin B = −(cos(A + B) − cos(A − B))/2
sin A cos B =(sin(A + B)+sin(A − B))/2
cos A cos B =(cos(A + B)+cos(A − B))/2
The following identities are for arbitrary triangles with side lengths a, b,andc,
each with an angle opposite it given by A, B, C, respectively (Figure 2.10):
sin A
a
=
sin B
b
=
sin C
c
(Law of sines)
c
2
= a
2
+ b
2
− 2ab cos C (Law of cosines)
a + b
a − b
=
tan
A+B
2
tan
A−B
2
(Law of tangents)
The area of a triangle can also be computed in terms of these side lengths:
Figure 2.10. Geometry for
triangle laws.
triangle area =
1
2
(a + b + c)(−a + b + c)(a − b + c)(a + b − c).

i
i
i
i
i
i
i
i
2.4. Vectors 21
2.4 Vectors
A vector describes a length and a direction. It can be usefully represented by an
arrow. Two vectors are equal if they have the same length and direction even if we
think of them as being located in different places (Figure 2.11). As much as pos-
sible, you should think of a vector as an arrow and not as coordinates or numbers.
At some point we will have to represent vectors as numbers in our programs, but
even in code they should be manipulated as objects and only the low-level vector
operations should know about their numeric representation (DeRose, 1989). Vec-
tors will be represented as bold characters, e.g., a. A vector’s length is denoted
a.Aunit vector is any vector whose length is one. The zero vector is the vector
of zero length. The direction of the zero vector is undefined.
Figure 2.11. These two
vectors are the same be-
cause they have the same
length and direction.
Vectors can be used to represent many different things. For example, they can
be used to store an offset, also called a displacement. If we know “the treasure is
buried two paces east and three paces north of the secret meeting place,” then we
know the offset, but we don’t know where to start. Vectors can also be used to
store a location, another word for position or point. Locations can be represented
as a displacement from another location. Usually there is some understood origin
location from which all other locations are stored as offsets. Note that locations
are not vectors. As we shall discuss, you can add two vectors. However, it usually
does not make sense to add two locations unless it is an intermediate operation
when computing weighted averages of a location (Goldman, 1985). Adding two
offsets does make sense, so that is one reason why offsets are vectors. But this
emphasizes that a location is not a offset; it is an offset from a specificorigin
location. The offset by itself is not the location.
2.4.1 Vector Operations
Vectors have most of the usual arithmetic operations that we associate with real
numbers. Two vectors are equal if and only if they have the same length and direc-
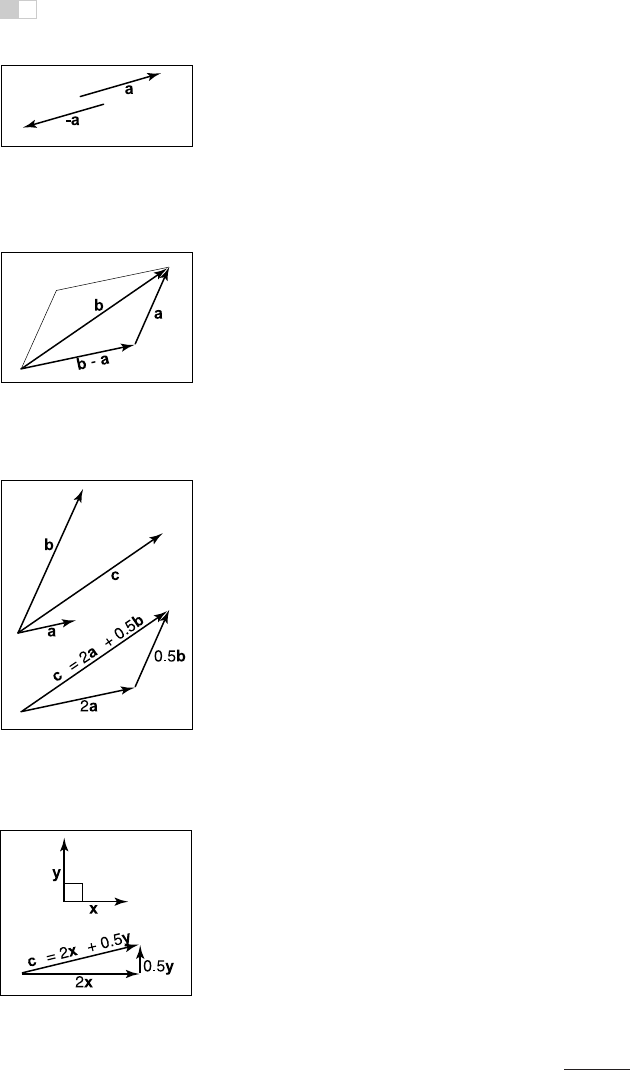
tion. Two vectors are added according to the parallelogram rule. This rule states
Figure 2.12. Two vec-
tors are added by arranging
them head to tail. This can
be done in either order.
that the sum of two vectors is found by placing the tail of either vector against the
head of the other (Figure 2.12). The sum vector is the vector that “completes the
triangle” started by the two vectors. The parallelogram is formed by taking the
sum in either order. This emphasizes that vector addition is commutative:
a + b = b + a.
Note that the parallelogram rule just formalizes our intuition about displacements.
Think of walking along one vector, tail to head, and then walking along the other.
i
i
i
i
i
i
i
i
22 2. Miscellaneous Math
The net displacement is just the parallelogram diagonal. You can also create a
unary minus for a vector: −a (Figure 2.13) is a vector with the same length as a
but opposite direction. This allows us to also define subtraction:
Figure 2.13. The vector
–a has the same length
but opposite direction of the
vector a.
b − a ≡−a + b.
You can visualize vector subtraction with a parallelogram (Figure 2.14). We can
write
a +(b − a)=b.
Vectors can also be multiplied. In fact, there are several kinds of products involv-
Figure 2.14. Vector sub-
traction is just vector addi-
tion with a reversal of the
second argument.
ing vectors. First, we can scale the vector by multiplying it by a real number k.
This just multiplies the vector’s length without changing its direction. For exam-
ple, 3.5a is a vector in the same direction as a but it is 3.5 times as long as a.We
discuss two products involving two vectors, the dot product and the cross prod-
uct, later in this section, and a product involving three vectors, the determinant, in
Chapter 5.
2.4.2 Cartesian Coordinates of a Vector
A 2D vector can be written as a combination of any two non-zero vectors which
are not parallel. This property of the two vectors is called linear independence.
Two linearly independent vectors form a 2D basis, and the vectors are thus re-
ferred to as basis vectors. For example, a vector c may be expressed as a combi-
nation of two basis vectors a and b (Figure 2.15):
c = a
c
a + b
c
b. (2.3)
Note that the weights a
c
and b
c
are unique. Bases are especially useful if the
Figure 2.15. Any 2D
vector c is a weighted sum
of any two non-parallel 2D
vectors a and b.
two vectors are orthogonal, i.e., they are at right angles to each other. It is even
more useful if they are also unit vectors in which case they are orthonormal.Ifwe
assume two such “special” vectors x and y are known to us, then we can use them
to represent all other vectors in a Cartesian coordinate system, where each vector
is represented as two real numbers. For example, a vector a might be represented
as
a = x
a
x + y
a
y,
where x
a
and y
a
are the real Cartesian coordinates of the 2D vector a (Fig-
ure 2.16). Note that this is not really any different conceptually from Equa-
tion (2.3), where the basis vectors were not orthonormal. But there are several
Figure 2.16. A2DCarte-
sian basis for vectors.
advantages to a Cartesian coordinate system. For instance, by the Pythagorean
theorem, the length of a is
a =
x
2
a
+ y
2
a
.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
