
i
i
i
i
i
i
i
i
2
Miscellaneous Math
Much of graphics is just translating math directly into code. The cleaner the math,
the cleaner the resulting code; so much of this book concentrates on using just the
right math for the job. This chapter reviews various tools from high school and
college mathematics and is designed to be used more as a reference than as a tu-
torial. It may appear to be a hodge-podge of topics and indeed it is; each topic
is chosen because it is a bit unusual in “standard” math curricula, because it is
of central importance in graphics, or because it is not typically treated from a ge-
ometric standpoint. In addition to establishing a review of the notation used in
the book, the chapter also emphasizes a few points that are sometimes skipped
in the standard undergraduate curricula, such as barycentric coordinates on tri-
angles. This chapter is not intended to be a rigorous treatment of the material;
instead intuition and geometric interpretation are emphasized. A discussion of
linear algebra is deferred until Chapter 5 just before transformation matrices are
discussed. Readers are encouraged to skim this chapter to familiarize themselves
with the topics covered and to refer back to it as needed. The exercises at the end
of the chapter may be useful in determining which topics need a refresher.
2.1 Sets and Mappings
Mappings, also called functions, are basic to mathematics and programming. Like
a function in a program, a mapping in math takes an argument of one type and
maps it to (returns) an object of a particular type. In a program we say “type;” in
13

i
i
i
i
i
i
i
i
14 2. Miscellaneous Math
math we would identify the set. When we have an object that is a member of a
set, we use the ∈ symbol. For example,
a ∈ S,
can be read “a is a member of set S.” Given any two sets A and B, we can create
a third set by taking the Cartesian product of the two sets, denoted A × B.This
set A × B is composed of all possible ordered pairs (a, b) where a ∈ A and
b ∈ B. As a shorthand, we use the notation A
2
to denote A × A. We can extend
the Cartesian product to create a set of all possible ordered triples from three sets
and so on for arbitrarily long ordered tuples from arbitrarily many sets.
Common sets of interest include:
• R—the real numbers;
• R
+
—the non-negative real numbers (includes zero);
• R
2
—the ordered pairs in the real 2D plane;
• R
n
—the points in n-dimensional Cartesian space;
• Z—the integers;
• S
2
—the set of 3D points (points in R
3
) on the unit sphere.
Note that although S
2
is composed of points embedded in three-dimensional
space, they are on a surface that can be parameterized with two variables, so it
can be thought of as a 2D set. Notation for mappings uses the arrow and a colon,
for example:
f : R → Z,
which you can read as “There is a function called f that takes a real number as
input and maps it to an integer.” Here, the set that comes before the arrow is called
the domain of the function, and the set on the right-hand side is called the target.
Computer programmers might be more comfortable with the following equivalent
language: “There is a function called f which has one real argument and returns
an integer.” In other words, the set notation above is equivalent to the common
programming notation:
Figure 2.1. A bijection
f
and the inverse function
f
−1
. Note that
f
–1
is also
a bijection.
integer f(real) ← equivalent → f : R → Z.
So the colon-arrow notation can be thought of as a programming syntax. It’s that
simple.
The point f(a) is called the image of a, and the image of a set A (a subset of
the domain) is the subset of the target that contains the images of all points in A.
The image of the whole domain is called the range of the function.
i
i
i
i
i
i
i
i
2.1. Sets and Mappings 15
2.1.1 Inverse Mappings
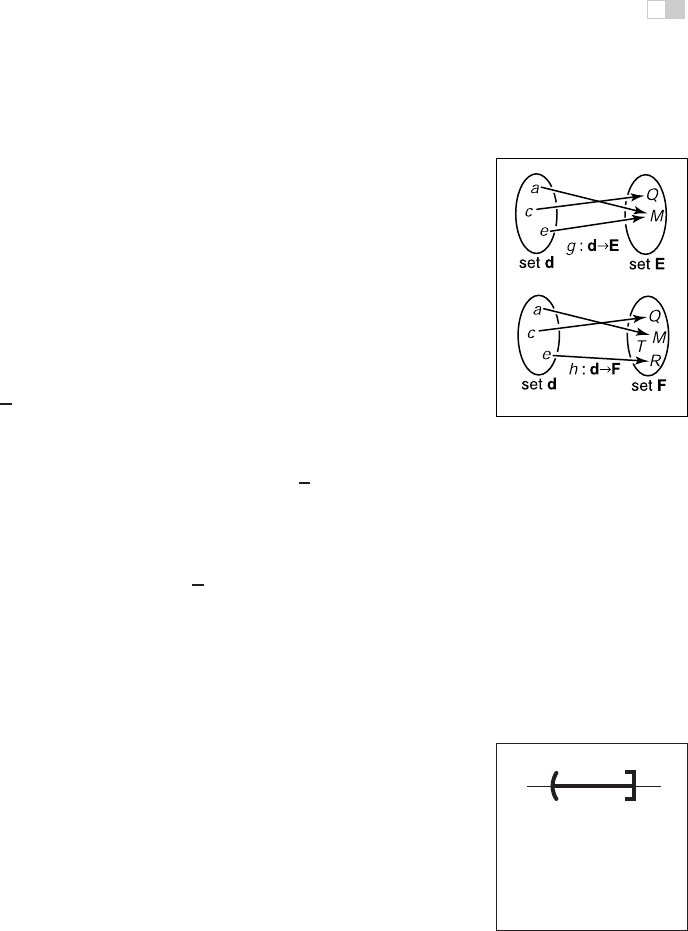
If we have a function f : A → B, there may exist an inverse function f
−1
: B →
A, which is definedbytherulef
−1
(b)=a where b = f (a).Thisdefinition only
works if every b ∈ B is an image of some point under f (that is, the range equals
the target) and if there is only one such point (that is, there is only one a for which
f(a)=b). Such mappings or functions are called bijections. A bijection maps
every a ∈ A to a unique b ∈ B, and for every b ∈ B, there is exactly one a ∈ A
such that f(a)=b (Figure 2.1). A bijection between a group of riders and horses
indicates that everybody rides a single horse, and every horse is ridden. The two
functions would be rider(horse) and horse(rider). These are inverse functions of
each other. Functions that are not bijections have no inverse (Figure 2.2).
An example of a bijection is f : R → R,with f (x)=x
3
.Theinverse
function is f
−1
(x)=
3
√
x. This example shows that the standard notation can be
Figure 2.2. The function
g
does not have an inverse
because two elements of d
map to the same element
of E. The function
h
has no
inverse because element
T
of F has no element of d
mapped to it.
somewhat awkward because x is used as a dummy variable in both f and f
−1
.It
is sometimes more intuitive to use different dummy variables, with y = f (x) and
x = f
−1
(y). This yields the more intuitive y = x
3
and x =
3
√
y. An example of a
function that does not have an inverse is sqr : R → R,wheresqr(x)=x
2
.This
is true for two reasons: first x
2
=(−x)
2
, and second no members of the domain
map to the negative portions of the target. Note that we can define an inverse if
we restrict the domain and range to R
+
.Then
√
x is a valid inverse.
2.1.2 Intervals
Often we would like to specify that a function deals with real numbers that are
restricted in value. One such constraint is to specify an interval. An example of
an interval is the real numbers between zero and one, not including zero or one.
We denote this (0, 1). Because it does not include its endpoints, this is referred
to as an open interval. The corresponding closed interval, which does contain its
endpoints, is denoted with square brackets: [0, 1]. This notation can be mixed, i.e.,
[0, 1) includes zero but not one. When writing an interval [a, b], we assume that
a ≤ b. The three common ways to represent an interval are shown in Figure 2.3.
The Cartesian products of intervals are often used. For example, to indicate that
a point x is in the unit cube in 3D, we say x ∈ [0, 1]
3
.
a < x < b
(a, b ]
a
b
_
Figure 2.3. Three equiv-
alent ways to denote the
interval from
a
to
b
that
includes
b
but not
a
.
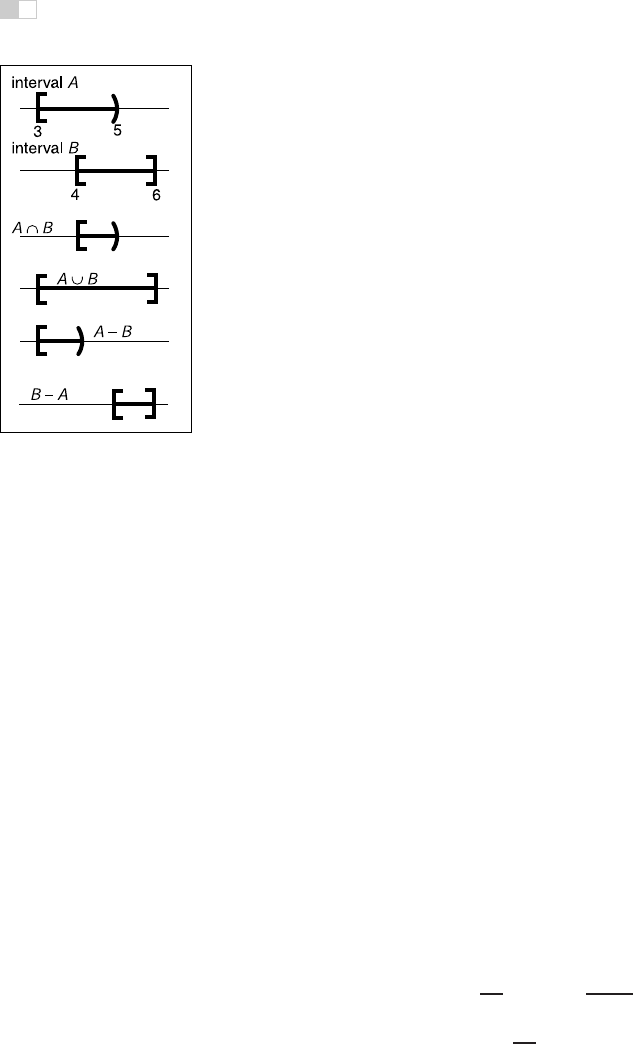
Intervals are particularly useful in conjunction with set operations: intersec-
tion, union,anddifference. For example, the intersection of two intervals is the
set of points they have in common. The symbol ∩ is used for intersection. For ex-
ample, [3, 5)∩[4, 6] = [4, 5). For unions, the symbol ∪ is used to denote points in
either interval. For example, [3, 5) ∪[4, 6] = [3, 6]. Unlike the first two operators,
the difference operator produces different results depending on argument order.
i
i
i
i
i
i
i
i
16 2. Miscellaneous Math
The minus sign is used for the difference operator, which returns the points in the
left interval that are not also in the right. For example, [3, 5) − [4, 6] = [3, 4) and
[4, 6] − [3, 5) = [5, 6]. These operations are particularly easy to visualize using
interval diagrams (Figure 2.4).
Figure 2.4. Interval opera-
tions on [3,5) and [4,6].
2.1.3 Logarithms
Although not as prevalent today as they were before calculators, logarithms are
often useful in problems where equations with exponential terms arise. By defi-
nition, every logarithm has a base a. The “log base a”ofx is written log
a
x and
is defined as “the exponent to which a must be raised to get x,” i.e.,
y =log
a
x ⇔ a
y
= x.
Note that the logarithm base a and the functionthat raises a to a power are inverses
of each other. This basic definition has several consequences:
a
log
a
(x)
= x;
log
a
(a
x
)=x;
log
a
(xy)=log
a
x +log
a
y;
log
a
(x/y)=log
a
x − log
a
y;
log
a
x =log
a
b log
b
x.
When we apply calculus to logarithms, the special number e =2.718 ... often
turns up. The logarithm with base e is called the natural logarithm. We adopt the
common shorthand ln to denote it:
ln x ≡ log
e
x.
Note that the “≡” symbol can be read “is equivalent by definition.” Like π,the
special number e arises in a remarkable number of contexts. Many fields use a par-
ticular base in addition to e for manipulations and omit the base in their notation,
i.e., log x. For example, astronomers often use base 10 and theoretical computer
scientists often use base 2. Because computer graphics borrows technology from
many fields we will avoid this shorthand.
The derivatives of logarithms and exponents illuminate why the natural loga-
rithm is “natural”:
d
dx
log
a
x =
1
x ln a
;
d
dx
a
x
= a
x
ln a.
The constant multipliers above are unity only for a = e.
i
i
i
i
i
i
i
i
2.2. Solving Quadratic Equations 17
2.2 Solving Quadratic Equations
A quadratic equation has the form
Ax
2
+ Bx + C =0,
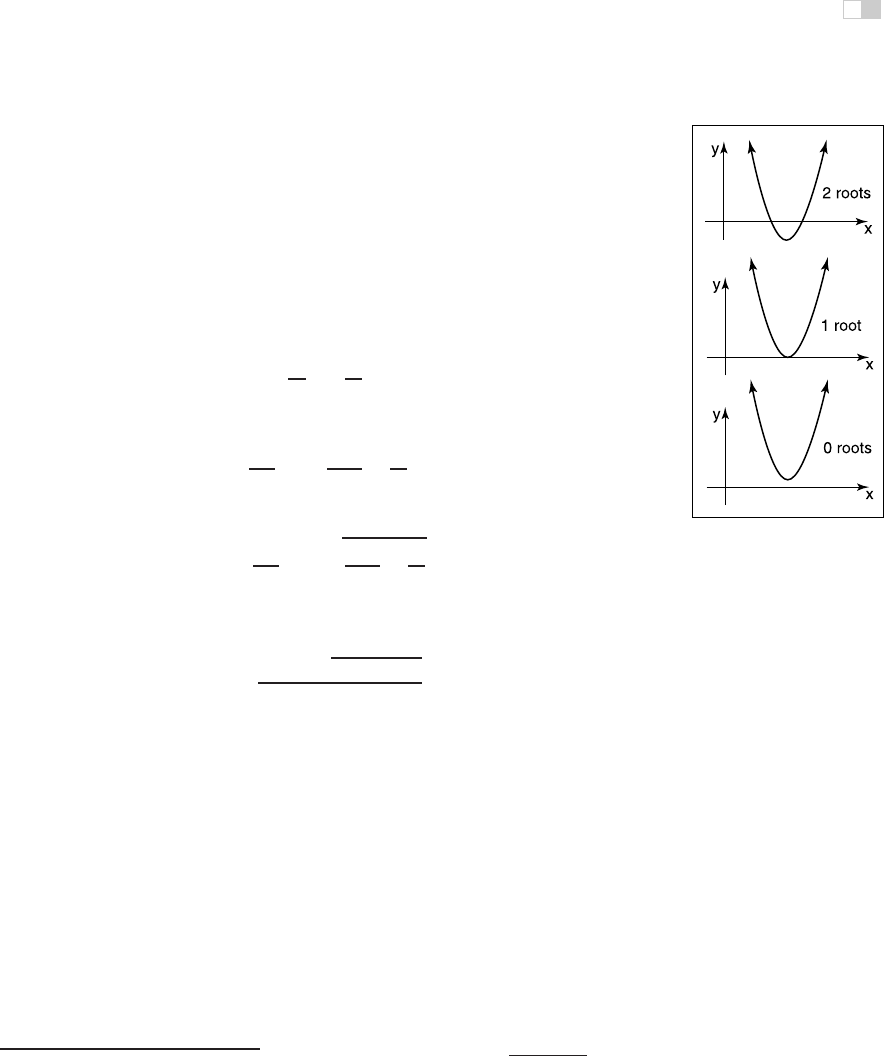
where x is a real unknown, and A, B,andC are known constants. If you think
of a 2D xy plot with y = Ax
2
+ Bx + C, the solution is just whatever x values
are “zero crossings” in y. Because y = Ax
2
+ Bx + C is a parabola, there will
be zero, one, or two real solutions depending on whether the the parabola misses,
grazes, or hits the x-axis (Figure 2.5).
To solve the quadratic equation analytically, we first divide by A:
x
2
+
B
A
x +
C
A
=0.
Then we “complete the square” to group terms:
x +
B
2A
2
−
B
2
4A
2
+
C
A
=0.
Moving the constant portion to the right-handside and taking the square root gives
Figure 2.5. The geometric
interpretation of the roots
of a quadratic equation is
the intersection points of a
parabola with the
x
-axis.
x +
B
2A
= ±
B
2
4A
2
−
C
A
.
Subtracting B/(2A) from both sides and grouping terms with the denominator
2A gives the familiar form:
1
x =
−B ±
√
B
2
− 4AC
2A
. (2.1)
Here the “±” symbol means there are two solutions, one with a plus sign and
one with a minus sign. Thus 3 ± 1 equals “two or four.” Note that the term that
determines the number of real solutions is
D ≡ B
2
− 4AC,
which is called the discriminant of the quadratic equation. If D>0,therearetwo
real solutions (also called roots). If D =0, there is one real solution (a “double”
root). If D<0, there are no real solutions.
For example, the roots of 2x
2
+6x +4=0are x = −1 and x = −2,andthe
equation x
2
+x+1has no real solutions. The discriminants of these equations are
D =4and D = −3, respectively, so we expect the number of solutions given.
In programs, it is usually a good idea to evaluate D first and return “no roots”
without taking the square root if D is negative.
1
A robust implementation will use the equivalent expression 2C/(−B ∓
√
B
2
− 4AC) to com-
pute one of the roots, depending on the sign of B (Exercise 7).
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
