i
i
i
i
i
i
i
i
2.4. Vectors 23
It is also simple to compute dot products, cross products, and coordinates of vec-
tors in Cartesian systems, as we’ll see in the following sections.
By convention we write the coordinates of a either as an ordered pair (x
a
,y
a
)
or a column matrix:
a =
x
a
y
a
.
The form we use will depend on typographic convenience. We will also occasion-
ally write the vector as a row matrix, which we will indicate as a
T
:
a
T
=
x
a
y
a
.
We can also represent 3D, 4D, etc., vectors in Cartesian coordinates. For the 3D
case, we use a basis vector z that is orthogonal to both x and y .
2.4.3 Dot Product
The simplest way to multiply two vectors is the dot product. The dot product of
a and b is denoted a · b and is often called the scalar product because it returns
a scalar. The dot product returns a value related to its arguments’ lengths and the
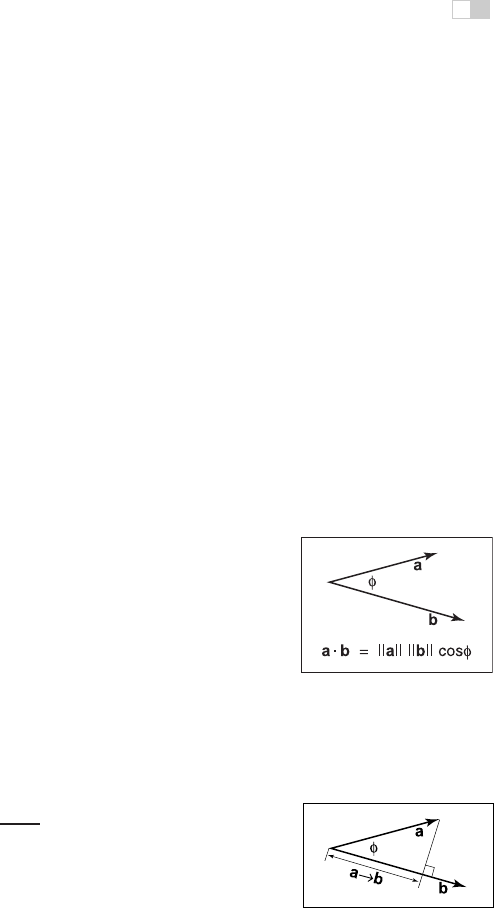
angle φ between them (Figure 2.17):
a · b = ab cos φ, (2.4)
The most common use of the dot product in graphics programs is to compute the
Figure 2.17. The dot
product is related to length
and angle and is one of the
most important formulas in
graphics.
cosine of the angle between two vectors.
The dot product can also be used to find the projection of one vector onto
another. This is the length a→b of a vector a that is projected at right angles onto
a vector b (Figure 2.18):
a→b = a cos φ =
a · b
b
. (2.5)
The dot product obeys the familiar associative and distributive properties we have
in real arithmetic:
Figure 2.18. The projec-
tion of a onto b is a length
found by Equation (2.5).
a · b = b · a,
a · (b + c)=a · b + a ·c, (2.6)
(ka) · b = a ·(kb)=ka · b.
If 2D vectors a and b are expressed in Cartesian coordinates, we can take ad-
vantage of x · x = y · y =1and x · y =0to derive that their dot product

i
i
i
i
i
i
i
i
24 2. Miscellaneous Math
is
a · b =(x
a
x + y
a
y) · (x
b
x + y
b
y)
= x
a
x
b
(x · x)+x
a
y
b
(x · y)+x
b
y
a
(y · x)+y
a
y
b
(y · y)
= x
a
x
b
+ y
a
y
b
.
Similarlyin3Dwecanfind
a · b = x
a
x
b
+ y
a
y
b
+ z
a
z
b
.
2.4.4 Cross Product
The cross product a × b is usually used only for three-dimensional vectors; gen-
eralized cross products are discussed in references given in the chapter notes. The
cross product returns a 3D vector that is perpendicular to the two arguments of
the cross product. The length of the resulting vector is related to sin φ:
a × b = absin φ.
The magnitude a×b is equal to the area of the parallelogram formed by vectors
a and b. In addition, a × b is perpendicular to both a and b (Figure 2.19). Note
Figure 2.19. The cross
product a × b is a 3D vector
perpendicular to both 3D
vectors a and b, and its
length is equal to the area
of the parallelogram shown.
that there are only two possible directions for such a vector. By definition, the
vectors in the direction of the x-, y- and z-axes are given by
x =(1, 0, 0),
y =(0, 1, 0),
z =(0, 0, 1),
and we set as a convention that x × y must be in the plus or minus z direction.
The choice is somewhat arbitrary, but it is standard to assume that
z = x × y.
All possible permutations of the three Cartesian unit vectors are
x × y =+z,
y ×x = −z,
y × z =+x,
z × y = −x,
z × x =+y,
x × z = −y .

i
i
i
i
i
i
i
i
2.4. Vectors 25
Because of the sin φ property, we also know that a vector cross itself is the
zero-vector, so x ×x = 0 and so on. Note that the cross product is not commuta-
tive, i.e., x ×y = y ×x. The careful observer will note that the above discussion
does not allow us to draw an unambiguous picture of how the Cartesian axes re-
late. More specifically, if we put x and y on a sidewalk, with x pointing East
and y pointing North, then does z point up to the sky or into the ground? The
usual convention is to have z point to the sky. This is known as a right-handed
coordinate system. This name comes from the memory scheme of “grabbing” x
with your right palm and fingers and rotating it toward y. The vector z should
align with your thumb. This is illustrated in Figure 2.20.
Figure 2.20. The “right-
hand rule” for cross prod-
ucts. Imagine placing the
base of your right palm
where a and b join at their
tails, and pushing the ar-
row of a toward b. Your ex-
tended right thumb should
point toward a × b.
The cross product has the nice property that
a × (b + c)=a × b + a × c,
and
a × (kb)=k(a × b).
However, a consequence of the right-hand rule is
a × b = −(b ×a).
In Cartesian coordinates, we can use an explicit expansion to compute the cross
product:
a × b =(x
a
x + y
a
y + z
a
z) × (x
b
x + y
b
y + z
b
z)
= x
a
x
b
x × x + x
a
y
b
x × y + x
a
z
b
x × z
+ y
a
x
b
y × x + y
a
y
b
y × y + y
a
z
b
y × z
+ z
a
x
b
z × x + z
a
y
b
z × y + z
a
z
b
z × z
=(y
a
z
b
− z
a
y
b
)x +(z
a
x
b
− x
a
z
b
)y +(x
a
y
b
− y
a
x
b
)z.
(2.7)
So, in coordinate form,
a × b =(y
a
z
b
− z
a
y
b
,z
a
x
b
− x
a
z
b
,x
a
y
b
− y
a
x
b
). (2.8)
2.4.5 Orthonormal Bases and Coordinate Frames
Managing coordinate systems is one of the core tasks of almost any graphics
program; key to this is managing orthonormal bases. Any set of two 2D vectors
u and v form an orthonormal basis provided that they are orthogonal (at right
angles) and are each of unit length. Thus,
u = v =1,

i
i
i
i
i
i
i
i
26 2. Miscellaneous Math
and
u · v =0.
In 3D, three vectors u, v,andw form an orthonormal basis if
u = v = w =1,
and
u · v = v · w = w · u =0.
This orthonormal basis is right-handed provided
w = u ×v,
and otherwise it is left-handed.
Note that the Cartesian canonical orthonormal basis is just one of infinitely
many possible orthonormal bases. What makes it special is that it and its implicit
origin location are used for low-level representation within a program. Thus,
the vectors x, y,andz are never explicitly stored and neither is the canonical
Figure 2.21. There is always a master or “canonical” coordinate system with origin o and
orthonormal basis x, y, and z. This coordinate system is usually defined to be aligned to the
global model and is thus often called the “global” or “world” coordinate system. This origin
and basis vectors are never stored explicitly. All other vectors and locations are stored with
coordinates that relate them to the global frame. The coordinate system associated with the
plane are explicitly stored in terms of global coordinates.
i
i
i
i
i
i
i
i
2.4. Vectors 27
origin location o. The global model is typically stored in this canonical coordinate
system, and it is thus often called the global coordinate system.However,ifwe
want to use another coordinate system with origin p and orthonormal basisvectors
u, v,andw,thenwedo store those vectors explicitly. Such a system is called
a frame of reference or coordinate frame. For example, in a flight simulator, we
might want to maintain a coordinate system with the origin at the nose of the
plane, and the orthonormal basis aligned with the airplane. Simultaneously, we
would have the master canonical coordinate system (Figure 2.21). The coordinate
system associated with a particular object, such as the plane, is usually called a
local coordinate system.
At a low level, the local frame is stored in canonical coordinates. For example,
if u has coordinates (x
u
,y
u
,z
u
),
u = x
u
x + y
u
y + z
u
z.
A location implicitly includes an offset from the canonical origin:
p = o + x
p
x + y
p
y + z
p
z,
where (x
p
,y
p
,z
p
) are the coordinates of p.
Note that if we store a vector a with respect to the u-v-w frame, we store a
triple (u
a
,v
a
,w
a
) which we can interpret geometrically as
a = u
a
u + v
a
v + w
a
w.
To get the canonical coordinates of a vector a stored in the u-v-w coordinate
system, simply recall that u, v,andw are themselves stored in terms of Cartesian
coordinates, so the expression u
a
u + v
a
v + w
a
w is already in Cartesian coordi-
nates if evaluated explicitly. To get the u-v -w coordinates of a vector b stored in
the canonical coordinate system, we can use dot products:
u
b
= u · b; v
b
= v · b; w
b
= w · b
This works because we know that for some u
b
, v
b
,andw
b
,
u
b
u + v
b
v + w
b
w = b,
and the dot product isolates the u
b
coordinate:
u · b = u
b
(u · u)+v
b
(u · v)+w
b
(u · w)
= u
b
This works because u, v,andw are orthonormal.
Using matrices to manage changes of coordinate systems is discussed in Sec-
tions 6.2.1 and 6.5.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
