
i
i
i
i
i
i
i
i
156 7. Viewing
7.4 Some Properties of the Perspective Transform
An important property of the perspective transform is that it takes lines to lines
and planes to planes. In addition, it takes line segments in the view volume to line
segments in the canonical volume. To see this, consider the line segment
q + t(Q − q).
When transformed by a 4 ×4 matrix M, it is a point with possibly varying homo-
geneous coordinate:
Mq + t(MQ − Mq) ≡ r + t(R −r).
The homogenized 3D line segment is
r + t(R − r)
w
r
+ t(w
R
− w
r
)
. (7.6)
If Equation (7.6) can be rewritten in a form
r
w
r
+ f(t)
R
w
R
−
r
w
r
, (7.7)
then all the homogenized points lie on a 3D line. Brute force manipulation of
Equation (7.6) yields such a form with
f(t)=
w
R
t
w
r
+ t(w
R
− w
r
)
. (7.8)
It also turns out that the line segments do map to line segments preserving the
ordering of the points (Exercise 8), i.e., they do not get reordered or “torn.”
A byproduct of the transform taking line segments to line segments is that
it takes the edges and vertices of a triangle to the edges and vertices of another
triangle. Thus, it takes triangles to triangles and planes to planes.
7.5 Field-of-View
While we can specify any window using the (l, r,b, t) and n values, sometimes
we would like to have a simpler system where we look through the center of the
window. This implies the constraint that
l = −r,
b = −t.
i
i
i
i
i
i
i
i
7.5. Field-of-View 157
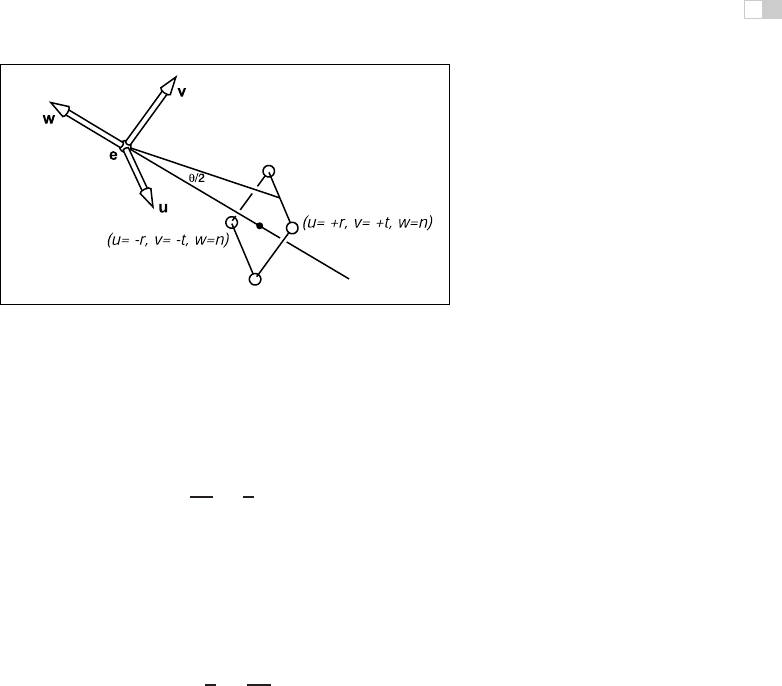
Figure 7.14. The field-of-view θ is the angle from the bottom of the screen to the top of the
screen as measured from the eye.
If we also add the constraint that the pixels are square, i.e., there is no distortion
of shape in the image, then the ratio of r to t must be the same as the ratio of the
number of horizontal pixels to the number of vertical pixels:
n
x
n
y
=
r
t
.
Once n
x
and n
y
are specified, this leaves only one degree of freedom. That is
often set using the field-of-view shown as θ in Figure 7.14. This is sometimes
called the vertical field-of-view to distinguish it from the angle between left and
right sides or from the angle between diagonal corners. From the figure we can
see that
tan
θ
2
=
t
|n|
.
If n and θ are specified, then we can derive t and use code for the more general
viewing system. In some systems, the value of n is hard-coded to some reasonable
value, and thus we have one fewer degree of freedom.
Frequently Asked Questions
• Is orthographic projection ever useful in practice?
It is useful in applications where relative length judgements are important. It can
also yield simplifications where perspective would be too expensive as occurs in
some medical visualization applications.
• The tessellated spheres I draw in perspective look like ovals. Is this a
bug?

i
i
i
i
i
i
i
i
158 7. Viewing
No. It is correct behavior. If you place your eye in the same relative position to
the screen as the virtual viewer has with respect to the viewport, then these ovals
will look like circles because they themselves are viewed at an angle.
• Does the perspective matrix take negative z values to positive z values
with a reversed ordering? Doesn’t that cause trouble?
Yes. The equation for transformed z is
z
= n + f −
fn
z
.
So z =+ is transformed to z
= −∞ and z = − is transformed to z = ∞.
So any line segments that span z =0will be “torn” although all points will be
projected to an appropriate screen location. This tearing is not relevant when all
objects are contained in the viewing volume. This is usually assured by clipping
to the view volume. However, clipping itself is made more complicated by the
tearing phenomenon as is discussed in Chapter 8.
• The perspective matrix changes the value of the homogeneous coordi-
nate. Doesn’t that make the move and scale transformations no longer
work properly?
Applying a translation to a homogeneous point we have
⎡
⎢
⎢
⎣
100t
x
010t
y
001t
z
000 1
⎤
⎥
⎥
⎦
⎡
⎢
⎢
⎣
hx
hy
hz
h
⎤
⎥
⎥
⎦
=
⎡
⎢
⎢
⎣
hx + ht
x
hy + ht
y
hz + ht
z
h
⎤
⎥
⎥
⎦
homogenize
−−−−−−−→
⎡
⎢
⎢
⎣
x + t
x
y + t
y
z + t
z
1
⎤
⎥
⎥
⎦
.
Similar effects are true for other transforms (see Exercise 5).
Notes
Most of the discussion of viewing matrices is based on information in Real-Time
Rendering (Akenine-M¨olleret al., 2008), the OpenGL Programming Guide (Shreiner
et al., 2004), Computer Graphics (Hearn & Baker, 1986), and 3D Game Engine
Design (Eberly, 2000).
i
i
i
i
i
i
i
i
7.5. Field-of-View 159
Exercises
1. Construct the viewport matrix required for a system in which pixel coordi-
nates count down from the top of the image, rather than up from the bottom.
2. Multiply the viewport and orthographic projection matrices, and show that
the result can also be obtained by a single application of Equation (6.7).
3. Derive the third row of Equation (7.3) from the constraint that z is preserved
for points on the near and far planes.
4. Show algebraically that the perspective matrix preserves order of z values
within the view volume.
5. For a 4×4 matrix whose top three rows are arbitrary and whose bottom row
is (0, 0, 0, 1), show that the points (x, y, z, 1) and (hx, hy, hz, h) transform
to the same point after homogenization.
6. Verify that the form of M
−1
p
given in the text is correct.
7. Verify that the full perspective to canonical matrix M
projection
takes (r, t, n)
to (1, 1, 1).
8. Write down a perspective matrix for n =1, f =2.
9. For the point p =(x, y, z, 1), what are the homogenized and unhomoge-
nized result for that point transformed by the perspective matrix in Exer-
cise 6?
10. For the eye position e =(0, 1, 0), a gaze vector g =(0, −1, 0),andaview-
up vector t =(1, 1, 0), what is the resulting orthonormal uvw basis used
for coordinate rotations?
11. Show, that for a perspective transform, line segments that start in the view
volume do map to line segments in the canonical volume after homogeniza-
tion. Further, show that the relative ordering of points on the two segments
is the same. Hint: Show that the f (t) in Equation (7.8) has the properties
f(0) = 0, f(1) = 1, the derivative of f is positive for all t ∈ [0, 1],andthe
homogeneous coordinate does not change sign.
i
i
i
i
i
i
i
i
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
