i
i
i
i
i
i
i
i
12.1. Triangle Meshes 271
Vertex {
// ... per-vertex data ...
Edge e; // any edge leaving vertex
}
In practice the Edge is stored by borrowing two bits of storage from the triangle
index t to store the edge index i, so that the total storage requirements remain the
same.
In this structure the neighbor array for a triangle tells which of the neighboring
triangles’ edges are shared with the three edges of that triangle. With this extra
information, we always know where to find the original triangle, which leads to
an invariant of the data structure: for any jth edge of any triangle t,
t.nbr[j].t.nbr[t.nbr[j].i].t == t.
Knowing which edge we came in through lets us know immediately which edge to
leave through in order to continue traversing around a vertex, leading to a stream-
lined algorithm:
TrianglesOfVertex(v) {
{t, i} = v.e;
do {
{t, i} = t.nbr[i];
} while (t != v.t);
}
The triangle-neighbor structure is quite compact. For a mesh with only vertex
positions, we are storing four numbers (three coordinates and an edge) per vertex
and six (three vertex indices and three edges) per face, for a total of 4n
v
+6n
t
≈
16n
v
units of storage per vertex, compared with 9n
v
for the basic indexed mesh.
The triangle neighbor structure as presented here works only for manifold
meshes, because it depends on returning to the starting triangle to terminate the
traversal of a vertex’s neighbors, which will not happen at a boundary vertex that
doesn’t have a full cycle of triangles. However, it is not difficult to generalize
it to manifolds with boundary, by introducing a suitable sentinel value (such as
−1) for the neighbors of boundary triangles and taking care that the boundary
vertices point to the most counterclockwise neighboring triangle, rather than to
any arbitrary triangle.
The Winged-Edge Structure
One widely used mesh data structure that stores connectivity information at the
edges instead of the faces is the winged-edge data structure. This data struc-
i
i
i
i
i
i
i
i
272 12. Data Structures for Graphics
e
0
e
1
e
2
e
12
e
13
e
14
e
15
e
3
e
4
e
5
e
6
e
7
e
8
e
9
e
10
e
18
e
16
e
17
e
19
e
3
e
4
[0]
[1]
[2]
…
ln rp lp rn
1423
180162
12130
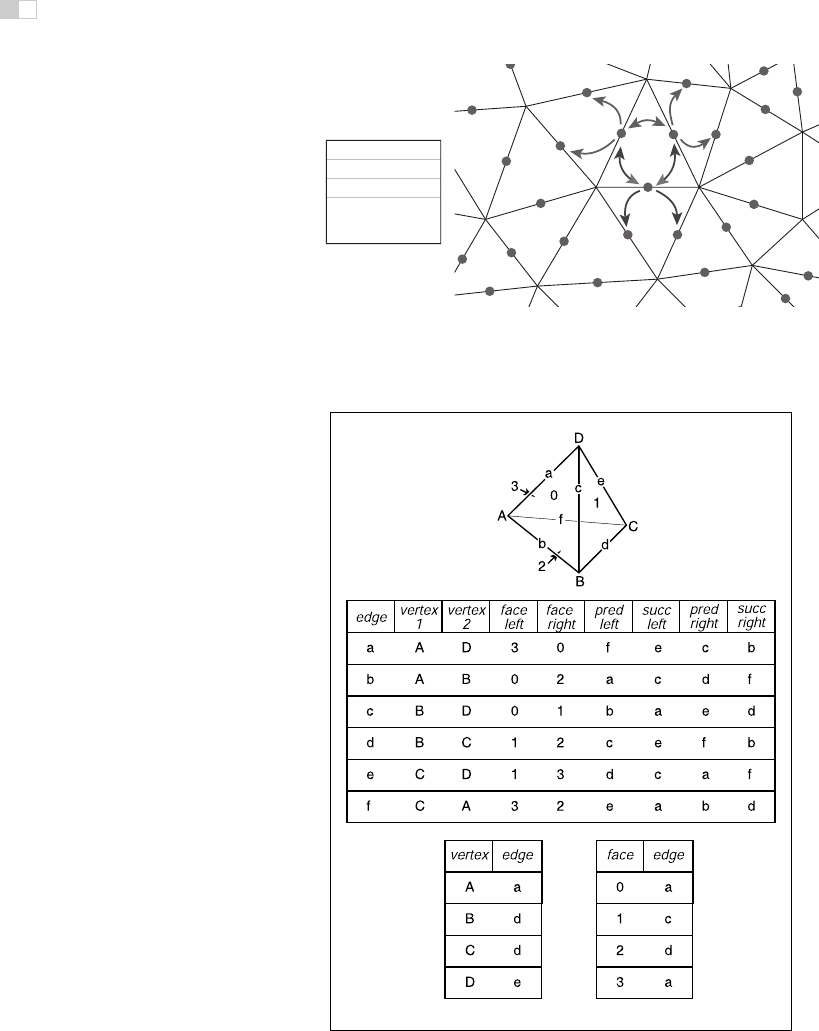
winged edge table
Figure 12.14. An example of a winged-edge mesh structure, stored in arrays.
Figure 12.15. A tetrahedron and the associated elements for a winged-edge data structure.
The two small tables are not unique; each vertex and face stores any one of the edges with
which it is associated.
i
i
i
i
i
i
i
i
12.1. Triangle Meshes 273
ture makes edges the first-class citizen of the data structure, as illustrated in Fig-
ures 12.14 and 12.15.
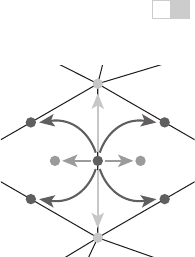
In a winged-edge mesh, each edge stores pointers to the two vertices it con-
nects (the head and tail vertices), the two faces it is part of (the left and right
faces), and, most importantly, the next and previous edges in the counterclock-
wise traversal of its left and right faces (Figure 12.16). Each vertex and face also
stores a pointer to a single, arbitrary edge that connects to it:
lnext
lprev
rprev
rnext
left right
head
tail
Figure 12.16. The refer-
ences from an edge to the
neighboring edges, faces,
and vertices in the winged-
edge structure.
Edge {
Edge lprev, lnext, rprev, rnext;
Vertex head, tail;
Face left, right;
}
Face {
// ... per-face data ...
Edge e; // any adjacent edge
}
Vertex {
// ... per-vertex data ...
Edge e; // any incident edge
}
The winged-edge data structure supports constant-time access to the edges of
a face or of a vertex, and from those edges the adjoining vertices or faces can be
found:
EdgesOfVertex(v) {
e = v.e;
do {
if (e.tail == v)
e = e.lprev;
else
e = e.rprev;
} while (e != v.e);
}
EdgesOfFace(f) {
e = f.e;
do {
if (e.left == f)
e = e.lnext;
else
e = e.rnext;

i
i
i
i
i
i
i
i
274 12. Data Structures for Graphics
} while (e != f.e);
}
These same algorithms and data structures will work equally well in a polygon
mesh that isn’t limited to triangles; this is one important advantage of edge-based
structures.
As with any data structure, the winged-edge data structure makes a variety of
time/space trade-offs. For example, we can eliminate the prev references. This
makes it more difficult to traverse clockwise around faces or counterclockwise
around vertices, but when we need to know the previous edge, we can always
follow the successor edges in a circle until we get back to the original edge. This
saves space, but it makes some operations slower. (See the chapter notes for more
information on these tradeoffs).
The Half-Edge Structure
The winged-edge structure is quite elegant, but it has one remaining awkward-
ness—the need to constantly check which way the edge is oriented before moving
to the next edge. This check is directly analogous to the search we saw in the basic
version of the triangle neighbor structure: we are looking to find out whether we
entered the present edge from the head or from the tail. The solution is also almost
indistinguishable: rather than storing data for each edge, we store data for each
half-edge. There is one half-edge for each of the two triangles that share an edge,
and the two half-edges are oriented oppositely, each oriented consistently with its
own triangle.
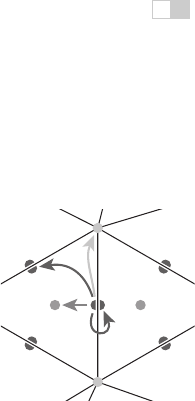
The data normally stored in an edge is split between the two half-edges. Each
half-edge points to the face on its side of the edge and to the vertex at its head, and
each contains the edge pointers for its face. It also points to its neighbor on the
h
0
h
3
h
5
h
6
h
1
h
4
h
2
h
9
h
10
hedge[0]
hedge[1]
hedge[2]
pair next
12
010
34
hedge[3]
29
hedge[4] 50
hedge[5]
…
46
Figure 12.17. An example of a half-edge mesh structure, stored in arrays.
i
i
i
i
i
i
i
i
12.1. Triangle Meshes 275
other side of the edge, from which the other half of the information can be found.
Like the winged-edge, a half-edge can contain pointers to both the previous and
next half-edges around its face, or only to the next half-edge. We’ll show the
example that uses a single pointer.
pair
next
head
left
Figure 12.18. The refer-
ences from a half-edge to
its neighboring mesh com-
ponents.
HEdge {
HEdge pair, next;
Vertex v;
Face f;
}
Face {
// ... per-face data ...
HEdge h; // any h-edge of this face
}
Vertex {
// ... per-vertex data ...
HEdge h; // any h-edge pointing toward this vertex
}
Traversing a half-edge structure is just like traversing a winged-edge structure
except that we no longer need to check orientation, and we follow the pair pointer
to access the edges in the opposite face.
EdgesOfVertex(v) {
h = v.h;
do {
h = h.pair.next;
} while (h != v.h);
}
EdgesOfFace(f) {
h = f.h;
do {
h = h.next;
} while (h != f.h);
}
The vertex traversal here is clockwise, which is necessary because of omitting
the prev pointer from the structure.
Because half-edges are generally allocated in pairs (at least in a mesh with
no boundaries), many implementations can do away with the pair pointers. For
instance, in an implementation based on array indexing (such as shown in Fig-
ure 12.17), the array can be arranged so that an even-numbered edge i always
pairs with edge i +1and an odd-numbered edge j always pairs with edge j − 1.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
