HIGHER-ORDER ELEMENTS 65
Node 2
Figure 3.8 Cubic elements
We can also define the cubic variation of the function u (the same
applies for q and the x,y coordinates) taking as unknowns the
function and its derivative at the two extreme nodes (Figure
3.7).
For
this case,
and,
u = φ
ι
η
ι
+ 0
2
Φι
<t>3
:i(£-l)
2
(£ +
2)
i(£ + l)
2
(£-2)
+ <M2 + 04
IF
φ
2
= -*/({-ΐ)*(ξ + ΐ)
04= -ΪΚξ
+
)
2
{ξ-)
(3.19)
3.4 ELEMENTS FOR THREE-DIMENSIONAL PROBLEMS
If the body
is
three dimensional the boundary elements are part of the
external surface of the body (Figure 3.9). They are usually of two
types:
quadrilateral and triangular elements. The functions used to
describe their geometry or the variables
u
and
q
over them are similar
to those used in finite elements.
In order to study these elements
we
need
first
to consider the
way
in
which
we
can pass from the
x,
y
9
z
global system to the system ξχ,ζ
2
,η
defined over the surface of the body.
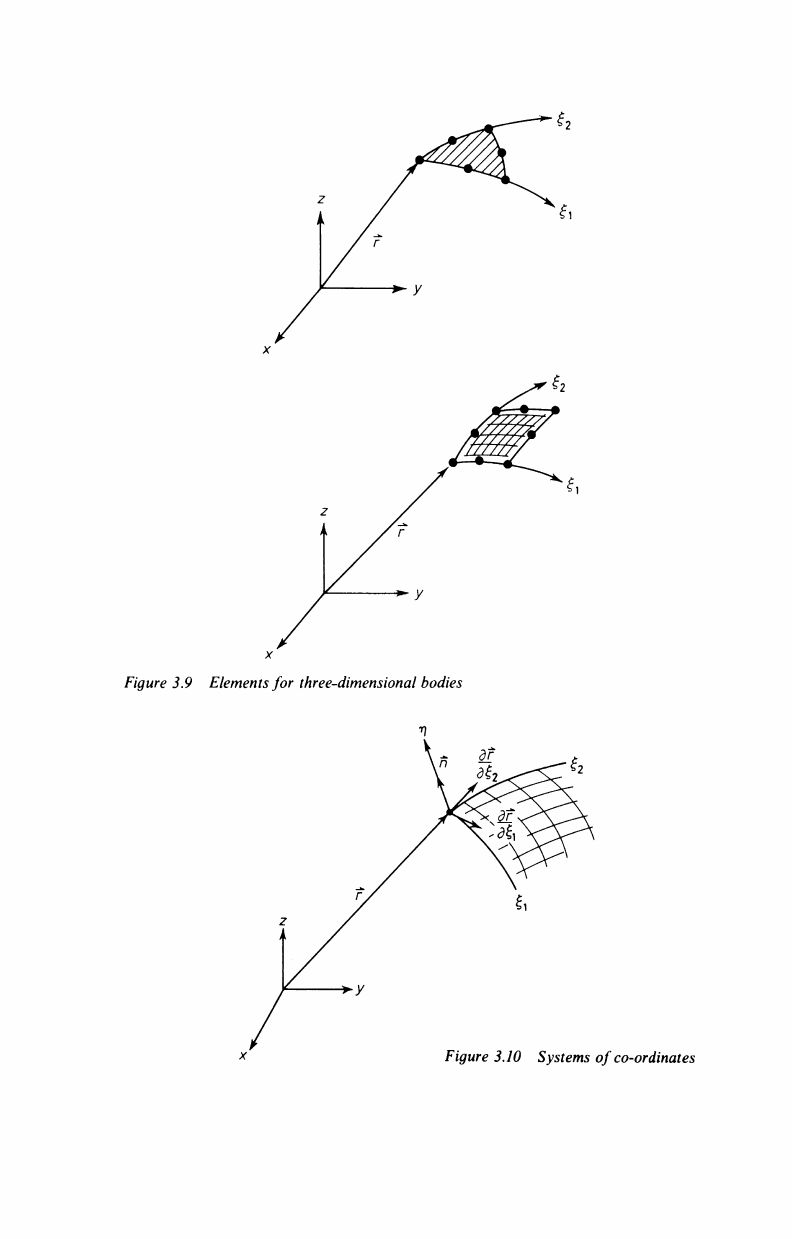
Figure 3.9
Elements
for three-dimensional bodies
Figure 3.10 Systems of co-ordinates

HIGHER-ORDER ELEMENTS 67
Consider the systems defined in Figure 3.10. For a function u, the
general transformation is given by
(3.20)
( du >
du
W
2
du
> =
~dx
dx
dx
dy
dy
8ξ
2
dy
δη
dz ~
dz
dz
di,j
<
(du ^
dx
du
dy~ 1
du
.. dz J
or,
rdu
N
3ξ~ι
du_
8ξ
2
du
<
dn
J
> = j<
( du
dx
dy
du
<
dz )
Hence we can find the inverse relationship, i.e.
( du^
d~x
du
1
sy
du
I dz)
►=J->«
( duX
WA
du
—
>
8ξ
2
du
. dr )
(3.21)
(3.22)
Having defined these relationships we can take for instance
~r
instead of u and define,
άΩ = d (volume) = magnitude of (
——
x
—·—
)άξ
ι
άξ
2
άη
dC
1
ΰζ
2
dr)
= (absolute value of
|
J |) άζ
γ
άξ
2
άη (3.23)
A differential of area (such as άΩ) for instance will be given by
d(area) =
dr dr
Wl
x
W
2
άξ,άξ
2
= �άξ
ι
άξ
2
(3.24)

68 HIGHER-ORDER ELEMENTS
where
dr
(dx
wrxäTi
dr
(dx
dy
'δίι
dy
8ξ
2
dz
οίι
dz
δξ~
2
Note that
| G |
is the magnitude of the normal vector,
dx dy dz
_, dr dr
~ dξ
1
d£
2
" δη' drf dr
where
Qi =
9i =
9s =
dy dz dy dz
dz dx dx dz
dx dy dy dx
The magnitude of
rt
gives the value of |G|, i.e.
|G|
= to?+flfi+ei)
1/2
These relationships will be used to integrate terms such as
u*gdr
and ug*dr
which now become,
The body force integrals like
f
bu*dQ
(3.25)
(3.26)
(3.27)
(3.28)
(3.29)
{ü*qGW&
2
;
[uq*GW&
2
(3.30)
(3.31)

HIGHER-ORDER ELEMENTS 69
will now become,
i<
οιι*μάζ
ι
άξ
2
άη
(3.32)
u, b and q are assumed to be functions of ξ
ί9
ξ
2
and η where
applicable.
QUADRILATERAL ELEMENTS
The simplest quadrilateral element is defined by its four corner points
(Figure 3.11). We can use a set of dimensionless coordinates
ξ
ί9
ξ
2
such that they vary from -
1
to -hi and the interpolation functions
0,. This allows us to write,
where the φ
ί
are,
01=4-(l-£l)(l-£
2
), *2=i(l+fl)(l-«2)
03 = id + ίι)(ΐ + ξ
2
04 = i(i - «i)(i + ξ
2
)
(3.33)
*~y
fi=-1
f
2
=
*1
.Cfi
f.= i
f
2
=-i
Dimensionless reference
system
Figure 3.11 Simplest quadrilateral element
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
